Антикризсное управление. Сборник задач по дисциплине антикризисное управление предприятием
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
Задача 15НПО «Полет» разрабатывает системы управления тактических ракет класса «земля – земля». Параметр точности попадания ракеты «в кол» можно оговорить двумя способами. Первый способ – это гарантировать максимальную ошибку попадания не более какой-то величины. При этом разработчик вынужден обеспечить себе какие-то технологические запасы по точности, что приведет к увеличению заявленной ошибки и снизит для потребителя привлекательность нового вооружения. Второй путь – это указать среднюю величину ошибки, которая будет заметна меньше гарантированной и более привлекательна. Пусть на основании расчетов и предыдущего опыта разработчики определили нормативную величину (среднюю М) погрешности в 10 м. При контрольных (типовых) испытаниях ракет после n = 10 пусков определили среднюю ошибку стрельбы тср в 10,5 м со стандартным отклонением S=1 м. Свидетельствуют ли результаты стрельбы, что система управления не соответствует техническим условиям, что необходимо проводить дорогостоящую ее доработку, а все ранее выпущенные ракеты вернуть на заводы-изготовители и оплатить рекламационные расходы? Решение. Поскольку нам не известна генеральная дисперсия σ, а лишь выборочное стандартное отклонение S, то наше стандартное распределение становится t-распределением Стьюдента с n = 10 степенями свободы. Нулевой гипотезой Н0 является предположение о том, что выборка была взята из генеральной совокупности с М = 10 м, альтернативной гипотезой Н1 – выборка не была взята из нормального распределения совокупности со средней М. Будем принимать решение при уровне значимости 5%. Используя таблицы t-распределения, находим, что граничное значение tгр 0,1/9 = 1,833. В этом подсчете взят 10-процентный уровень значимости (0,1), исходя из того, что он делится на две части по 5%, а количество свобод n– 1 = 9. Здесь проверочной статистикой является tпр: 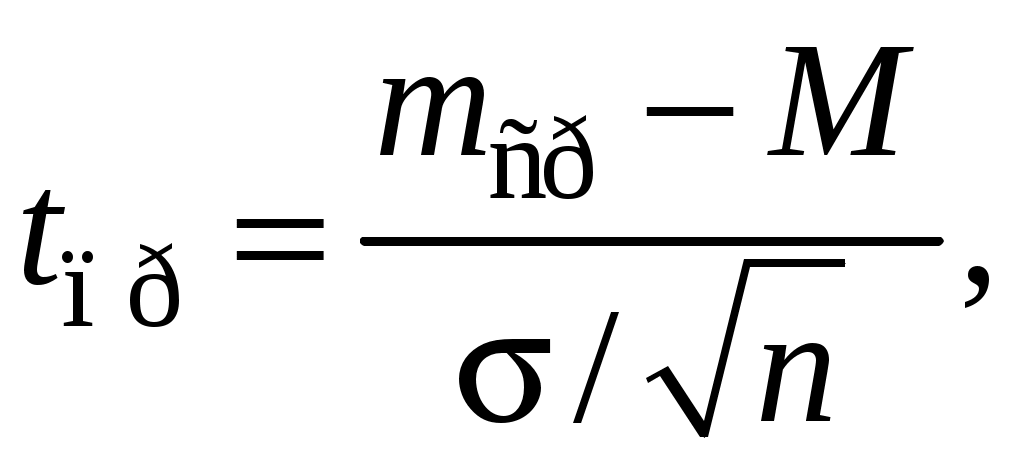 где где 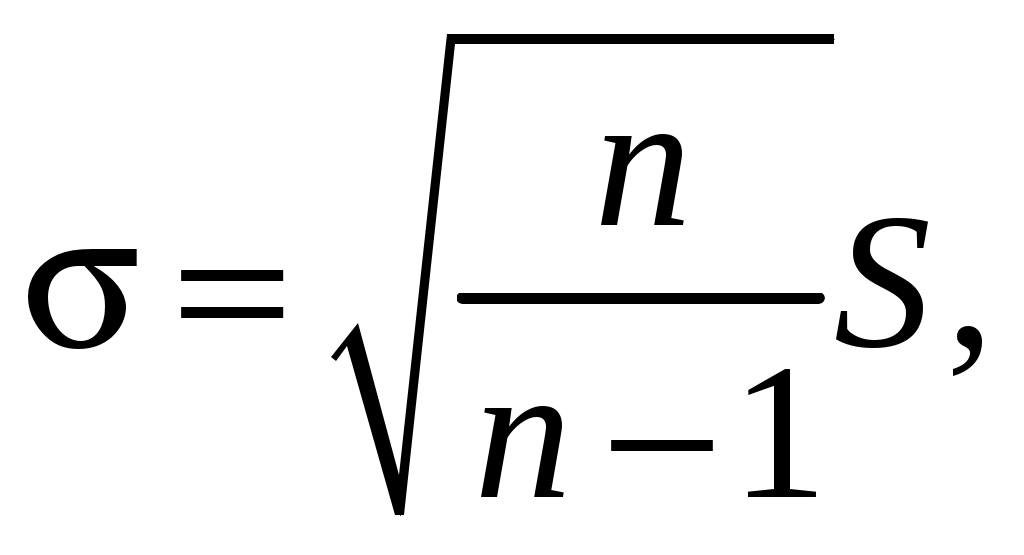 или 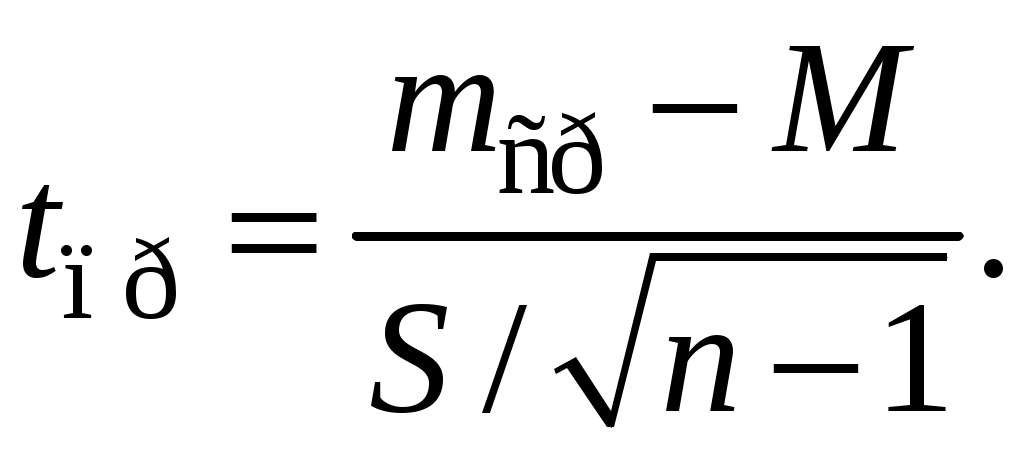 После подстановки численных значений получим: 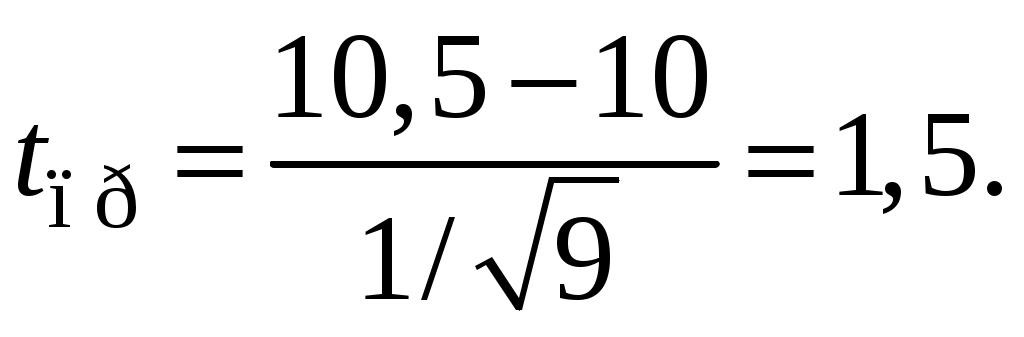 Поскольку tпр<tгр, принимаем нулевую гипотезу, то есть дорабатывать систему управления не следует, НПО «Полет» не понесет убытков, его устойчивому положению не угрожает кризис. Задача 16В ОКБ полупроводниковых приборов освоен массовый выпуск новых диодов Ганна. На производстве налажен контроль за процессом изготовления и испытания диодов таким образом, чтобы доля неисправной продукции р не превышала 3%. Из контролируемой партии диодов в 600 шт. 30 диодов оказались не соответствующими ТУ. Имеется ли основание предполагать, что производственный процесс вышел из-под контроля, что производится много неисправных диодов и необходимо изменить технологический процесс, поменять или модернизировать оборудование? Решение. Случайная величина – отказ диодов – подчиняется биномиальному распределению, так как исход испытания бинарный: годен-негоден. В то же время объем выборки в 600 шт. большой и биномиальное распределение можно аппроксимировать посредством нормального распределения со средней долей р = 0,03. Структурная ошибка выборочного распределения: 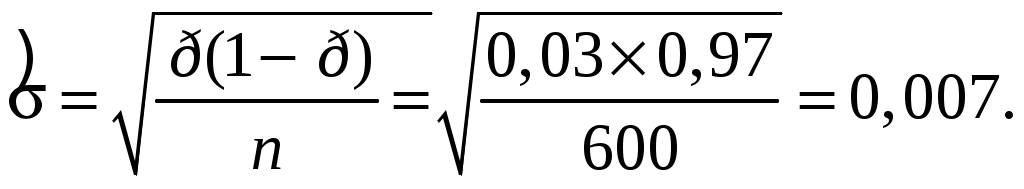 Доля дефектов в выборке Будем испытывать гипотезу Н0 на уровне значимости 5%. Из примера 1 мы имеем Zгр = 1,645. Проверочная статистика: 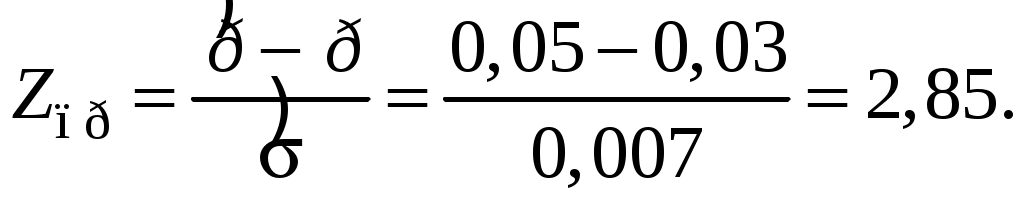 На основании того, что Zпр > Zгр, отклоняем нулевую гипотезу и делаем вывод, что ОКБ необходимо откорректировать технологический процесс выпуска диодов, так как иначе вырастут рекламации, штрафы, что может снизить кризисустойчивость предприятия. |
