Антикризсное управление. Сборник задач по дисциплине антикризисное управление предприятием
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
Задача 12Распределение общей суммы инвестиций между проектами с разной прибыльностью Перед руководителем компании стоит задача по распределению инвестиций в сумме S=10 млн.руб для увеличения выпуска продукции. Четыре заместителя руководителя (по производству, технологии, капитальному строительству, снабжению) предлагают набор мероприятий, ориентированных на различный прирост выпуска продукции и требующих соответствующих капитальных затрат. Каждый из заместителей готов взяться за реализацию любого, но одного (j-го) мероприятия из всего набора ( Необходимо решить проблему распределения выделенных средств (N), обеспечив максимальный прирост выпуска продукции Таблица 3
Рассматриваемый вариант распределения инвестиций Процесс такого решения чрезвычайно трудоемок и значительно усложняется по мере увеличения числа проектов ( Разработаем математическую модель рассматриваемой задачи для решения ее в MS Excel. Представим совокупность всех решений задачи матрицей. Таблица 4 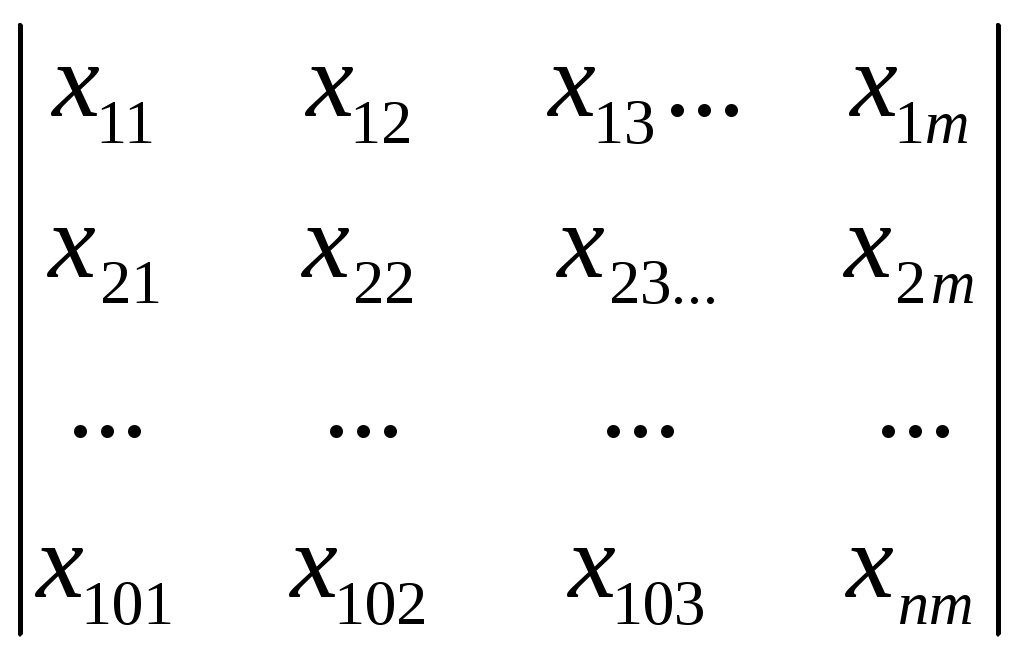 (5) (5)Решения Запишем целевую функцию задачи: где Здесь каждый элемент Ограничения запишем из следующих соображений: Сумма Второе ограничение должно учитывать тот факт, что сумма всех инвестиций по всем проектам должна быть равна 10 млн.руб. Это можно записать в следующем виде: В целом математическая модель задачи может быть представлена в виде: Целевая функция: Ограничения: 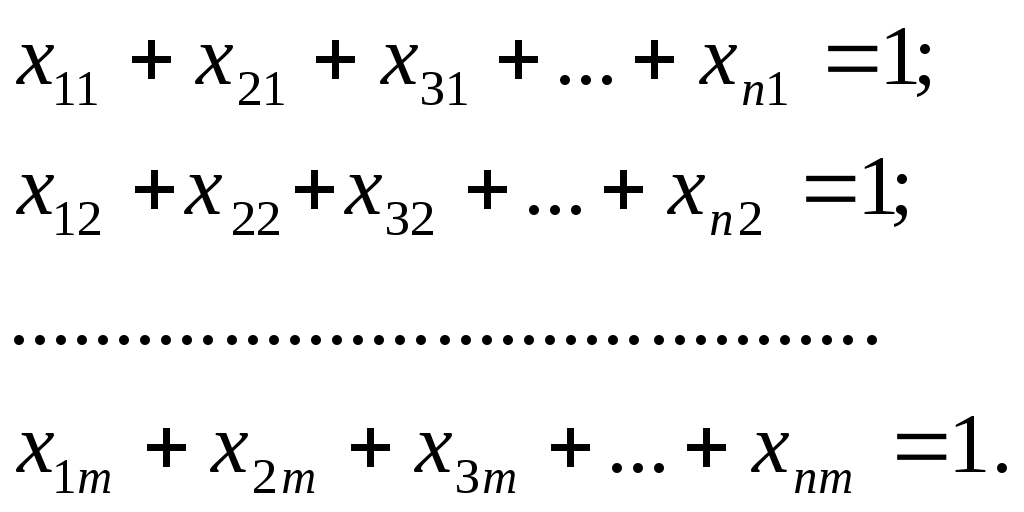 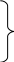 (7) (7) 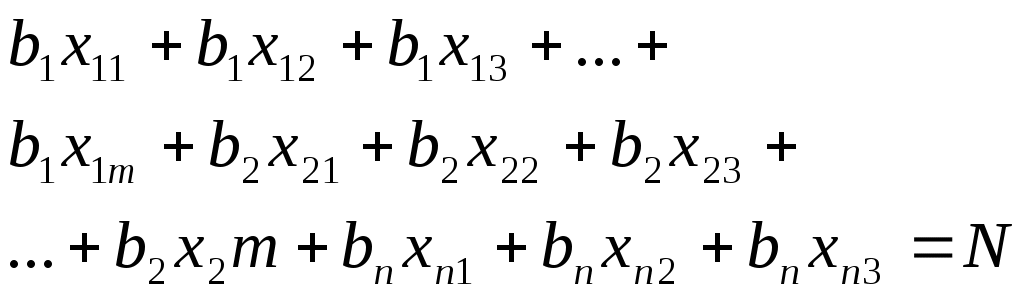 (8) (8)Решение математической модели (6,7,8,9) в системе MS Excel дает следующие результаты для данных в табл.3; N=10 млн. руб.; 1 проект – 2 млн.руб.; 2 проект – 2 млн. руб.; 3 проект – 4 млн.руб.; 4 проект – 2 млн.руб. Полученные результаты совпадают с результатами, где решение определялось «вручную» методом поэтапного (пошагового) наращивания числа рассматриваемых сфер использования распределяемого ресурса. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
