Антикризсное управление. Сборник задач по дисциплине антикризисное управление предприятием

• Название: Сборник задач по дисциплине антикризисное управление предприятием
• Дата: 11.11.2021
• Размер: 1.29 Mb.
• Имя файла: Антикризсное управление.doc
• Тип: Сборник задач; #269788
• страница: 8 из 24

Задача 9

Для целей прогнозирования устойчивости предприятия с горизонтом в один год необходимо иметь информацию об итоговой балльной оценке предприятия за 3-4 предыдущих года. Информация за более длительный предыдущий период только для стабильно работающих предприятий может иметь какую-то ценность. Для остальных предприятий эти более ранние промежутки отягощены случайными факторами, влияющими на экономические показатели, характерными для экономики переходного периода [4-6].

В табл.2 приведено в качестве примера изменение суммарного количества баллов для пяти инновационных предприятий г. Томска за последние 6 лет.

Таблица 2

Суммарное значение баллов по шести годам для пяти инновационных предприятий г.Томска

Годы
№	1	2	3	4	5	6
1	34,3	34,5	33,9	43,2	32,7	32,5
2	12,6	16,8	16,2	10,6	13,8	13,6
3	95,6	88	97,6	97,0	96,6	96,8
4	79,7	48,1	83,9	75,0	84,6	80,0
5	11,6	10,6	13,0	14,3	37	24,2

Таблица 3

Результаты прогнозного расчета

№	α	Ф7	Δ Ф7 (0,9)	Δ Ф7(0,95)	Δ Ф7З.С.	Δ Ф7сред.	класс
1	0,9	32,5	33,5±0,64	33,5±0,82	35,0	33,9	4
2	0,85	13,52	13,9±1,6	13,9±2,0	14,0	13,6	4
3	0,90	96,82	95,5±2,4	95,5±3,1	95,0	96,3	1-2
4	0,67	88,2	77±4,2	77±5,3	74,4	81,0	2
5	0,5	23,94	17,3±7,3	17,3±9,2	17,9	21,8,	4-5

Оценим прогнозное значение баллов для каждого из предприятий тремя методами: экспоненциального сглаживания, «золотого сечения» и методом наименьших квадратов.

Метод экспоненциального сглаживания

Метод предложен Р.Брауном [3] и заключается в использовании рекуррентной формулы (1) для вычисления прогнозного значения ( ) переменной величины - в нашем случае суммарное количество баллов; – год.

, (1)

где – параметр сглаживания:

,

здесь – число членов динамического ряда, которые желательно принять во внимание при расчете .

Уровни стационарного динамического ряда колеблются вокруг некоторого среднего значения. Прогнозирование сводится к поиску этого среднего значения. Чем успешнее осуществляется этот поиск, тем меньше будут ошибки прогноза.

Поскольку на практике не всегда очевидным бывает выбор , то мы предлагаем выбирать по результатам наиболее точного прогнозирования последнего значения фактической переменной , используя в формуле (2) оставшиеся значения динамического ряда:

(2)

Найденное таким образом значение (табл.1) используется затем в формуле (1) для прогнозирования величины : в нашем случае – количество баллов за седьмой год.

Полученные прогнозные значения, конечно, с каким-то отклонением могут соответствовать будущим фактическим значениям переменной . Следовательно, вполне правомерно задаться вопросом с какой вероятностью мы сможем определить поле разброса (доверительный интервал) для каждого из предприятий и предсказать их класс.

Для решения этого вопроса используем распределение Стьюдента.

Распределение Стьюдента зависит от параметра – объема выборки (в нашем случае =7) и не зависит от неизвестных параметров нормального распределения – математического ожидания и среднеквадратичного отклонения; эта особенность является его большим достоинством.

Доверительный интервал, в котором находится прогнозируемое значение баллов 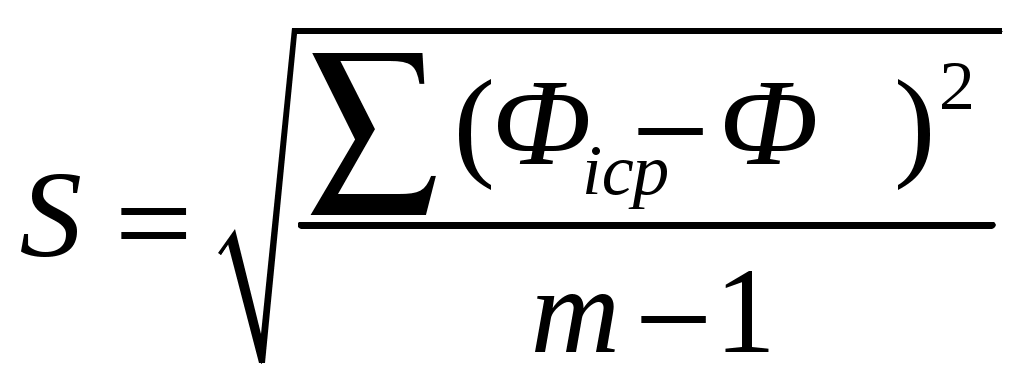определяется по формуле [2]:

, (3)

где - среднее значение баллов за семь лет конкретного предприятия;

- критерий Стьюдента при вероятности γ и степени свободы -1.

(Для = 0,9 и -1=6, =1,94. Для = 0,95 и -1=6, =2,45).

- «исправленное» среднеквадратичное отклонение:

Результаты расчета по формуле (3) для всех предприятий приведены в табл. 2, из которой следует, что полученные прогнозные значения попадают в доверительные интервалы, рассчитанные с вероятностью 0,9 и 0,95.

Метод «золотого сечения»

Основан на известном с древних времен гармоничного деления целого на части [8]:

Целое (100 %)=часть 1 (62%)+часть 2 (38%).

Наличие этой, вроде бы, элементарной, пропорции, с легкой руки Леонардо да Винчи названной золотым сечением, лежит в основе «стержня» устойчивости всех мировых явлений [8].

Суть предлагаемого метода заключается в следующем. Вначале производится сглаживание ряда для каждого предприятия с помощью скользящей средней [3]:



Полученный сглаженный ряд делим на две части в пропорции к от конца ряда. То есть в нашем случае четыре последних значения ряда и и два первых - и .

Определяем среднее значение для каждой из групп.

Среднее значение баллов для первой группы ( 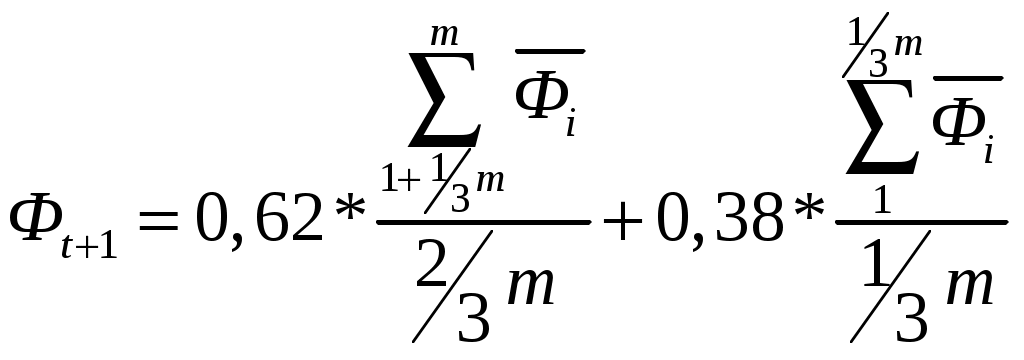) умножаем на коэффициент 0,62, а среднее значение для второй группы ( ) умножаем на 0,38. Просуммировав полученные результаты, определяем прогнозное значение .

, (4)

Рассчитанное по формуле (4) прогнозное значение баллов для каждого предприятия представлены в табл. 3, из которой следует, что вновь полученные прогнозные значения по методу «Золотого сечения» также попадают в зону допуска прогноза для обеих вероятностей.

Метод наименьших квадратов.

Метод основан на аналитическом описании сглаженного ряда значений суммарных баллов для каждого из пяти предприятий. Прогнозные значения вычисляются по полученным формулам при подстановке .

Ниже приводятся аппроксимирующие функции 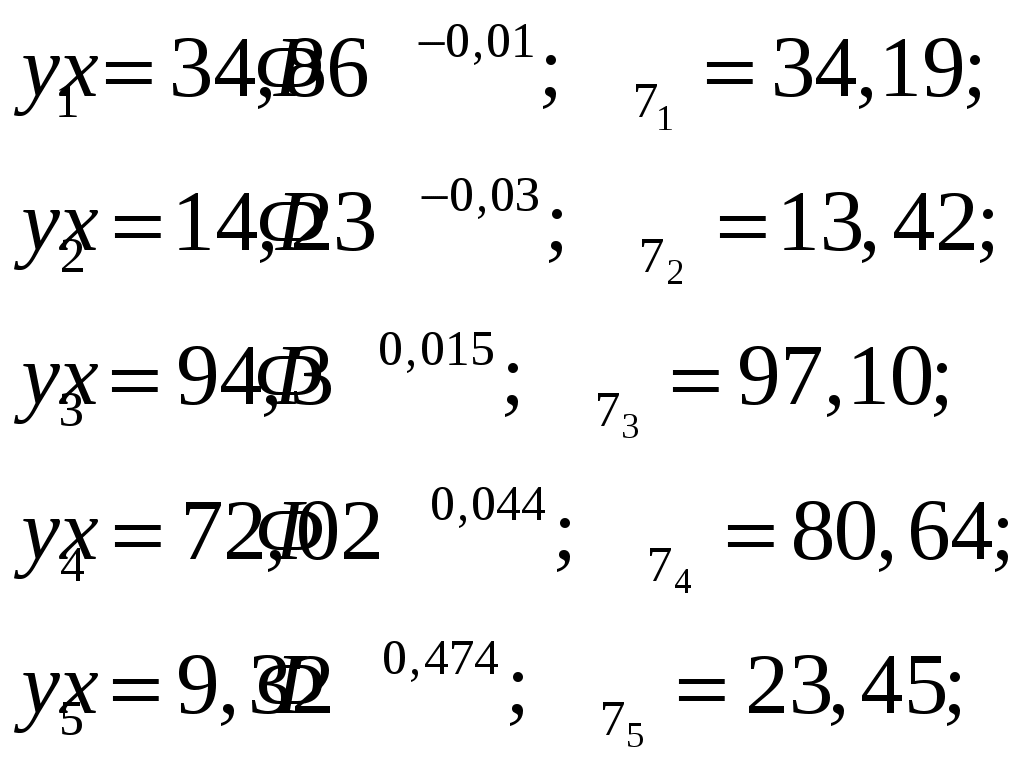(5) для каждого из пяти предприятий и расчетное значение . Функции получены с помощью программного продукта Excel.

(5)

Анализ полученных значений показывает, что они находятся в зоне допуска прогноза табл.3

Для окончательного решения вопроса о прогнозной величине баллов для каждого предприятия можно найти среднее значение по трём методам расчёта, как наиболее достоверного.