Антикризсное управление. Сборник задач по дисциплине антикризисное управление предприятием

• Название: Сборник задач по дисциплине антикризисное управление предприятием
• Дата: 11.11.2021
• Размер: 1.29 Mb.
• Имя файла: Антикризсное управление.doc
• Тип: Сборник задач; #269788
• страница: 3 из 24

3. Прогнозирование дебиторской кризисустойчивости при коммерциализации разработок

В инновационном менеджменте финансовая кризисустойчивость может рассматриваться в двух аспектах. Во-первых, инвестора интересует кризисустойчивость инновационной фирмы, чтобы обезопасить свои инвестиции и получить на них доход; поставщиков интересует, сумеет ли инновационная фирма рассчитаться за поставки материалов, сырья, комплектующих без предоплаты (кредиторская задолженность). Во-вторых, инновационную фирму интересует, сумеют ли клиенты, покупатели рассчитаться за поставленную им продукцию без предоплаты (дебиторская задолженность), – в целях расширения круга потребителей нового изделия.

Из всех возможных финансовых показателей для данной цели, пожалуй, лучше всего подходит коэффициент текущей ликвидности (КТЛ), который предназначен для характеристики платежеспособности предприятий:



где – ликвидные активы: денежные средства и ценные бумаги; дебиторская задолженность; запасы сырья и незавершенная продукция соответственно;

– пассивы: кредиторская задолженность и краткосрочные кредиты банка соответственно.

В Постановлении правительства РФ от 20 мая 1994 г. № 498 «О некоторых мерах по реализации законодательства о несостоятельности предприятий» указывается, что гарантией полной платежеспособности является двукратное превышение ликвидных активов над краткосрочными обязательствами ( ).

Понятно, что фирмы с КТЛ<1 можно столь же четко отнести к явным банкротам, ибо у них ликвидных активов меньше, чем долгов. Остается еще одна группа предприятий, у которых 1<КТЛ<2. О них нельзя сказать с полной определенностью, вернут или не вернут они долги своим партнерам. Ответ на этот вопрос (прогноз) можно дать лишь с той или иной степенью вероятности. Оценить ее можно несколькими приемами. Ниже мы рассмотрим те из них, которые наиболее легки для практического использования.

Прогнозирование с помощью неравенства Чебышева. Неравенство Чебышева имеет следующий вид: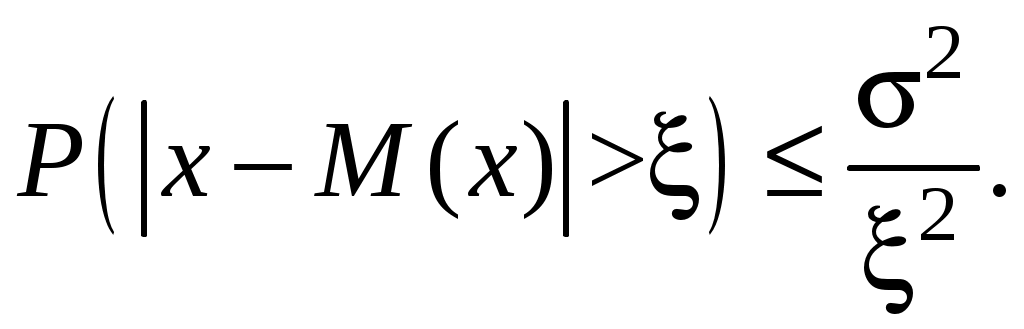

Оно позволяет находить верхнюю границу того, что случайная величина х отклонится в обе стороны от своего среднего значения М(х) на величину больше ξ. Эта величина равна или меньше, чем 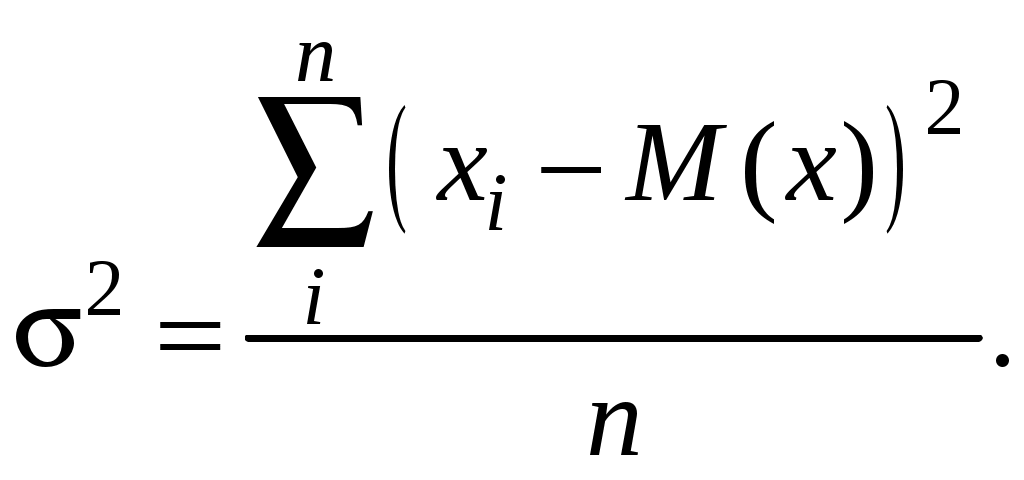, где ² – дисперсия случайной величины х, определяемая по формуле



Нас интересует вероятность отклонения только в одну сторону (в большую), поэтому вышеприведенное неравенство Чебышева надо переписать следующим образом: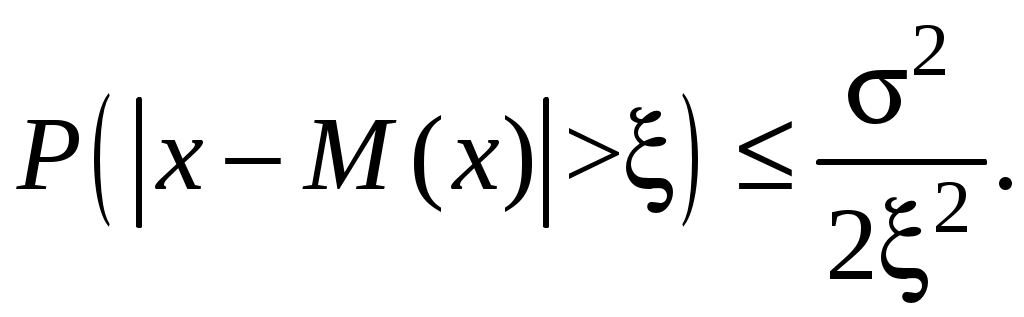

(4.7)

Задача 3

Инвестор решает вопрос о вложении средств под быстро реализуемый и перспективный проект венчурной фирмы. Для этого он изучил изменение КТЛ фирмы за последние четыре полугодия и получил следующие данные: 1,6; 2,2; 1,8; 1,6.

Инвестор решает вопрос: какова вероятность того, что фирма восстановит свою платежеспособность, т.е. КТЛ  2?

Определяется дисперсия КТЛ: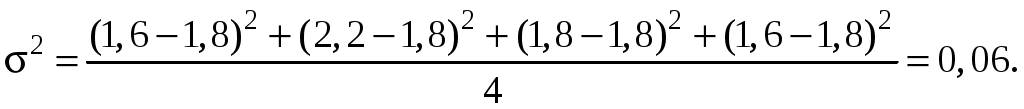



Используя формулу (4.7), получим: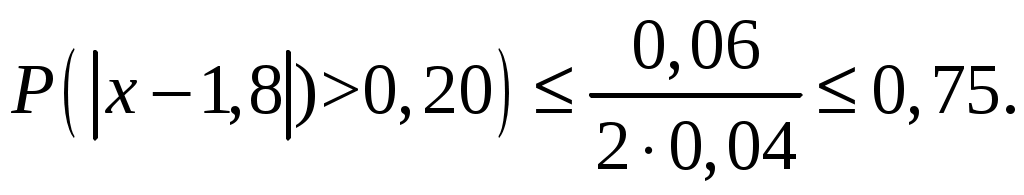



Полученная вероятность восстановления платежеспособности фирмы достаточно обнадеживающая. Поскольку инвестор собирается взаимодействовать с венчурной фирмой, значит, он склонен к риску и полученная вероятность должна его удовлетворить.

Большим достоинством неравенства Чебышева является то, что оно пригодно для употребления при любом количестве наблюдений и любом законе распределения вероятностей.

Платой за отсутствие жестких ограничений является некоторая неопределенность оценок уровня вероятностей.