Задача 2. Седьмая математическое ожидание дискретной случайной величины

• Название: Седьмая математическое ожидание дискретной случайной величины
• Анкор: Задача 2.doc
• Дата: 27.04.2017
• Размер: 1.95 Mb.
• Имя файла: Задача 2.doc
• Тип: Глава; #5986
• страница: 3 из 7

Глава девятая

ЗАКОН БОЛЬШИХ ЧИСЕЛ
§ 1. Предварительные замечания
Как уже известно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые невозможно. Казалось бы, поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли (имеются и другие теоремы, которые здесь не рассматриваются). Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли—простейшим. Для доказательства этих теорем мы воспользуемся неравенством Чебышева.
§ 2. Неравенство Чебышева
Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин. Для простоты ограничимся доказательством этого неравенства для дискретных величин.

Рассмотрим дискретную случайную величину X, заданную таблицей распределения:

X	x1	X2	…	xn
p	p1	P2	…	pn

Поставим перед собой задачу оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа . Если  достаточно мало, то мы оценим, таким образом, вероятность того, что Xпримет значения, достаточно близкие к своему математическому ожиданию. П. Л. Чебышев доказал неравенство, позволяющее дать интересующую нас оценку.

Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа , не меньше, чем 1—D(Х)/²:

Р(|Х —М(Х)|<)1—D(X)/².

Доказательство. Так как события, состоящие в осуществлении неравенств |Х—М(Х)|<и|Х—М(Х)|, противоположны, то сумма их вероятностей равна единице, т. е.

Р(|Х —М(Х)|<)+ Р(|Х —М(Х)|)= 1.

Отсюда интересующая нас вероятность

Р(|Х —М(Х)|<)=1- Р(|Х —М(Х)|). (*)

Таким образом, задача сводится к вычислению вероятности Р (| Х—М(Х)| ).

Напишем выражение дисперсии случайной величины X:

D(X)=[x₁-M(X)]²p₁+[x₂-M(X)]²p₂+…+[x_n-M(X)]2p_n.

Очевидно, все слагаемые этой суммы неотрицательны.

Отбросим те слагаемые, у которых |x_i—M(Х)|< (для оставшихся слагаемых |x_j—M(Х)|), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено kпервых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом,

D(X)[x_k+1-M(Х)]²p_k+1 + [x_k+2-M(X)]²p_k+z+ ... +[x_n-M(X)]²p_n.

Заметим, что обе части неравенства |x_j — М (Х)|  (j = k+1, k+ 2, ..., п)положительны, поэтому, возведя их в квадрат, получим равносильное неравенство |x_j — М (Х)|² ^ Воспользуемся этим замечанием и, заменяя в оставшейся сумме каждый из множителей |x_j — М (Х)|² числом ^ (при этом неравенство может лишь усилиться), получим

D(X) ^ (р_к+1+ p_k+2 + … + р_n). (**)

По теореме сложения, сумма вероятностей р_к+1+ p_k+2 + … + р_nесть вероятность того, что X примет одно, безразлично какое, из значений x_k+1, х_к+2,....х_п, а при любом из них отклонение удовлетворяет неравенству |x_j — М (Х)|  Отсюда следует, что сумма р_к+1+ p_k+2 + … + р_n выражает вероятность

P(|X — М (Х)| 

Это соображение позволяет переписать неравенство (**) так:

D(X) ^ P(|X — М (Х)|  ,

или

P(|X — М (Х)|  D(X) / ² (***)

Подставляя (***) в (*), окончательно получим

P(|X — М (Х)| < 1- D(X) / ²,

что и требовалось доказать.

Замечание. Неравенство Чебышева имеет для практики ограниченное значение поскольку часто дает грубую, а иногда и тривиальную (не представляющую интереса) оценку. Например, если D(X)>² и, следовательно, D(X)/²>1, то 1— D(Х)/² < 0; таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения неотрицательна, а это и без того очевидно, так как любая вероятность выражается неотрицательным числом.

Теоретическое же значение неравенства Чебышева весьма велико. Ниже мы воспользуемся этим неравенством для вывода теоремы Чебышева.
§ 3. Теорема Чебышева
Теорема Чебышева. Если Х₁, Х₂,…, Х_n, ...—попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число е, вероятность неравенства



будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы



Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Доказательство. Введем в рассмотрение новую случайную величину — среднее арифметическое случайных величин

=(X₁+X₂+…+X_n)/n.

Найдем математическое ожидание . Пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), получим

M= . (*)

Применяя к величине 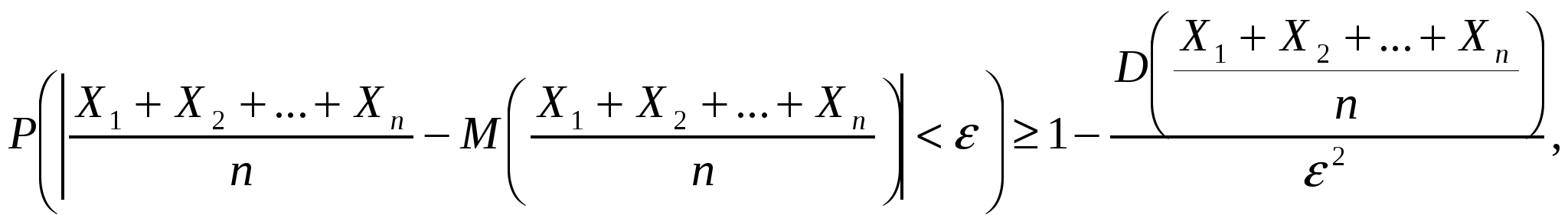неравенство Чебышева, имеем



или, учитывая соотношение (*),

(**)

Пользуясь свойствами дисперсии (постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат; дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых), получим

.

По условию дисперсии всех случайных величин ограничены постоянным числом С, т. е. имеют место неравенства: D(X₁) C; D(X₂) C; ...; D(X_n) C, поэтому

(D(X₁)+ D(X₂)+…+D(X_n))/n² (C+C+…+C)/n²=nC/n²=C/n.

Итак,

.(***)

Подставляя правую часть (***) в неравенство (**) (отчего последнее может быть лишь усилено), имеем



Отсюда, переходя к пределу при , получим



Наконец, учитывая, что вероятность не может превышать единицу, окончательно можем написать



Теорема доказана.

Выше, формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Очевидно, что если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева.

Обозначим математическое ожидание каждой из случайных величин через а; в рассматриваемом случае среднее арифметическое математических ожиданий, как легко видеть, также равно а. Мы можем сформулировать теорему Чебышева для рассматриваемого частного случая.

Если Х₁, Х₂, ..., Х_п ,... —попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число  > О, вероятность неравенства



будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы будет иметь место равенство


§ 4. Сущность теоремы Чебышева
Сущность доказанной теоремы такова: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу (М (X₁)+ М(Х₂) +...+М (Х_п))/п (или к числу а в частном случае). Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.

Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое.

Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.

Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин; она является ярким примером, подтверждающим справедливость учения диалектического материализма о связи между случайностью и необходимостью.
§ 5. Значение теоремы Чебышева для практики
Приведем примеры применения теоремы Чебышева к решению практических задач.

Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос дает теорема Чебышева (ее частный случай).

Действительно, рассмотрим результаты каждого измерения как случайные величины Х₁, Х₂, ..., Х_п. К этим величинам можно применить теорему Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же математическое ожидание, 3) дисперсии их равномерно ограничены.

Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных. Второе требование выполняется, если измерения произведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру а. Третье требование выполняется, если прибор обеспечивает определенную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их ограничено.

Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом п вероятность неравенства

|(Х₁+ Х₂+ ...+ Х_п)/n-a|<

как угодно близка к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины.

Итак, теорема Чебышева указывает условия, при которых описанный способ измерения может быть применен. Однако ошибочно думать, что, увеличивая число измерений, можно достичь сколь угодно большой точности. Дело в том, что сам прибор дает показания лишь с точностью ±; поэтому каждый из результатов измерений, а следовательно, и их среднее арифметическое будут получены лишь с точностью, не превышающей точности прибора.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.

В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.

Уже из приведенных примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.
§ 6. Теорема Бернулли
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Можно ли предвидеть, какова примерно будет относительная частота появлений события? Положительный ответ на этот вопрос дает теорема, доказанная Якобом Бернулли (опубликована в 1713 г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П. Л. Чебышевым в 1846 г.

Теорема Бернулли. Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если  — сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство



Доказательство. Обозначим через Х₁дискретную случайную величину — число появлений события в первом испытании, через Х₂— во втором, ..., Х_п—в п-миспытании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие не появилось) с вероятностью 1— p = q.

Можно ли применить к рассматриваемым величинам теорему Чебышева? Можно, если случайные величины попарно независимы и дисперсии их ограничены. Оба условия выполняются. Действительно, попарная независимость величин Х₁, Х₂, . . ., Х_пследует из того, что испытания независимы. Дисперсия любой величины Х_i(i= 1,2, . .., п)равна произведению pq(Это следует из § 6 гл.III,если принять n=1); так как p+q= 1, то произведение pqне превышает (Известно, что произведение двух сомножителей, сумма которых есть величина постоянная, имеет наибольшее значение при равенстве сомножителей. Здесь сумма p_i+q_i=1, т.е. постоянна, поэтому при p_i=q_i=1/2 произведение p_iq_iимеет наибольшее значение и равно 1/4) 1/4 и, следовательно, дисперсии всех величин ограничены, например, числом С =1/4.

Применяя теорему Чебышева (частный случай) к рассматриваемым величинам, имеем



Приняв во внимание, что математическое ожидание а каждой из величин X_i; (т. е. математическое ожидание числа появлений события в одном испытании) равно вероятности р наступления события (см. гл. VII, § 2, пример 2), получим



Остается показать, что дробь (Х₁+ Х₂+ ...+ Х_п)/n равна относительной частоте т/п появлений события А в испытаниях. Действительно, каждая из величин Х₁, Х₂, .. ., Х_ппри появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма Х₁+ Х₂+ ...+ Х_п равна числу т появлений события в п испытаниях, а значит,

(Х₁+ Х₂+ ...+ Х_п)/n=m/n.

Учитывая это равенство, окончательно получим



Замечание. Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р; другими словами, из теоремы Бернулли не вытекает равенство В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании.

Таким образом, сходимость относительной частоты т/п к вероятности р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности»(Последовательность случайных величин Х₁,Х₂,...сходится по вероятности к случайной величине X, если для любого >0вероятность неравенства |X_n-X|<при стремится к единице). Точнее, различие между указанными видами сходимости состоит в следующем: если т/п стремится при к р как пределу в смысле обычного анализа, то начиная с некоторого n = Nи для всех последующих значений п неуклонно выполняется неравенство | т/п—р | < ; если же т/п стремится по вероятности к р при , то для отдельных значений п неравенство может не выполняться.

Итак, теорема Бернулли утверждает, что при относительная частота стремится по вероятности к р. Коротко теорему Бернулли записывают так:

.

Как видим, теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности (см. гл. I, § 6—7).
Задачи
1. Сформулировать и записать теорему Чебышева, используя понятие «сходимости по вероятности».

2.Используя неравенство Чебышева, оценить вероятность того, что |Х—М(Х)|<0,1, если. D(X)= 0,001.

Отв. PO,9.

3.Дано: Р (| Х—М (X)| < )0,9;D(X) = 0,004. Используя неравенство Чебышева, найти .

Отв. 0,2.