Задача 2. Седьмая математическое ожидание дискретной случайной величины

• Название: Седьмая математическое ожидание дискретной случайной величины
• Анкор: Задача 2.doc
• Дата: 27.04.2017
• Размер: 1.95 Mb.
• Имя файла: Задача 2.doc
• Тип: Глава; #5986
• страница: 7 из 7

Глава тринадцатая

ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ
§ 1. Определение показательного распределения
Показательным (экспоненциальным)называют распределение вероятностей непрерывной случайной величины Х₁которое описывается плотностью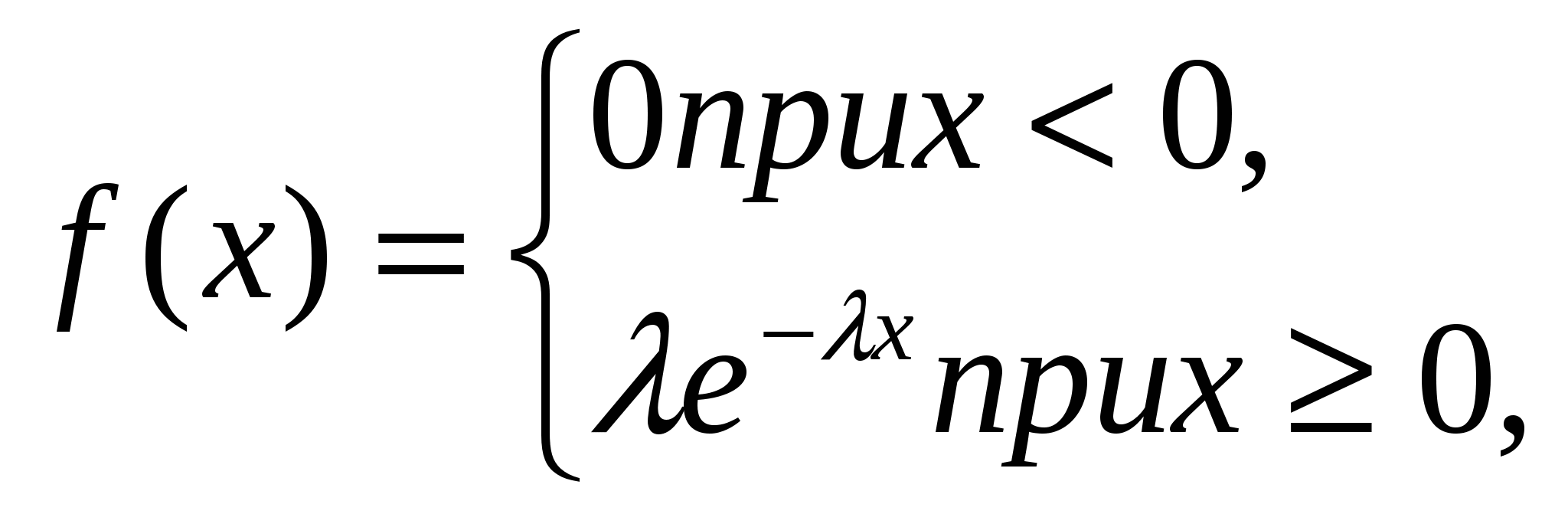



где  — постоянная положительная величина.

Мы видим, что показательное распределение определяется одним параметром . Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большею числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или три и т. д. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока (см. § 5).

Найдем функцию распределения показательного закона (см. гл. XI, § 3):



Итак,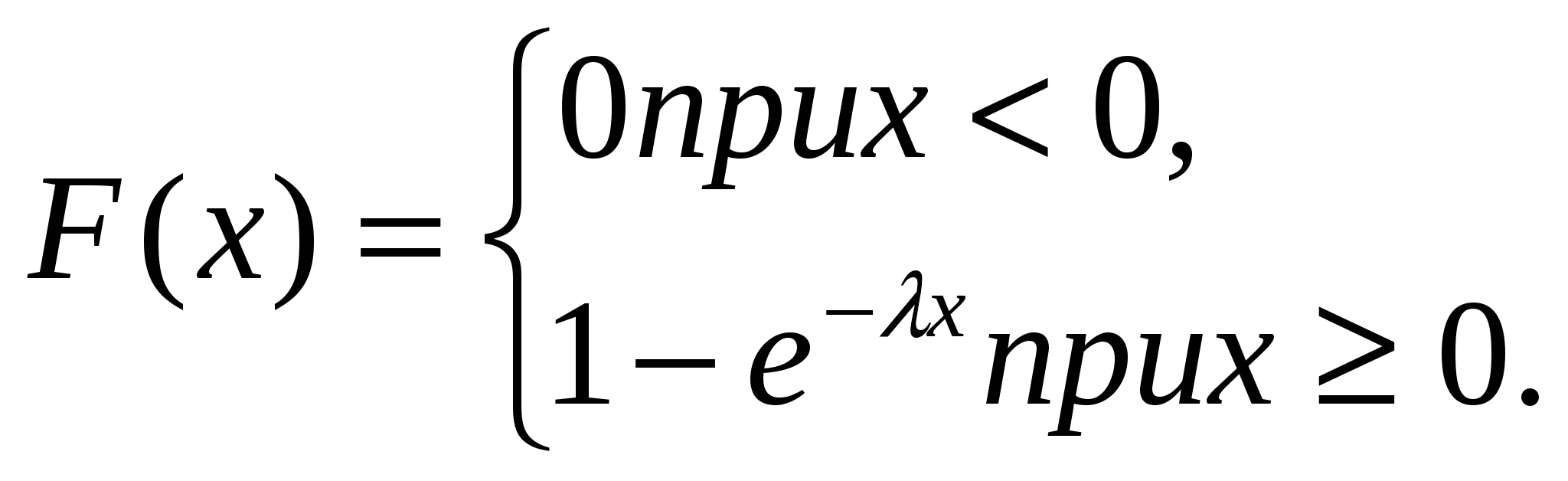



Мы определили показательный закон с помощью плотности распределения; ясно, что его можно определить, используя функцию распределения.

Графики плотности и функции распределения показательного закона изображены на рис. 12.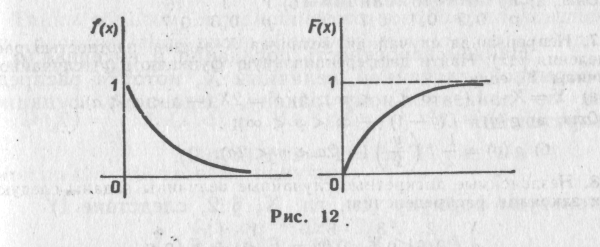



Пример. Написать плотность и функцию распределения показательного закона, если параметр = 8.

Решение. Очевидно, искомая плотность распределения

f(х) = 8е^-8x при х0; f(x)=Oпри х < 0.

Искомая функция распределения

F(x) =1—e^-8xпри x0; F(x) = 0 при х < 0.
§ 2. Вероятность попадания в заданный интервал показательно распределенной случайной величины
Найдем вероятность попадания в интервал (а,b)непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения



Используем формулу (см. гл. X, § 2, следствие 1)

P(a<X<b) = F(b) — F(a).

Учитывая, что F(а)=,F(b)=,получим

P(a<X<b) = (*)

Значения функции е^-xнаходят по таблице.

Пример. Непрерывная случайная величина Xраспределена по показательному закону

f(x)=2e^-2xпри х 0; f(x)=0 при х < 0.

Найти вероятность того, что в результате испытания Xпопадает в интервал (0,3, 1).

Решение. По условию,  = 2. Воспользуемся формулой (*):

Р (0,3 < X < 1)=е^-(2*0,3)-е^-(2*1)=е^-0,6-е^-2 = 0,54881—0,135340,41.
§ 3. Числовые характеристики показательного распределения
Пусть непрерывная случайная величина Xраспределена по показательному закону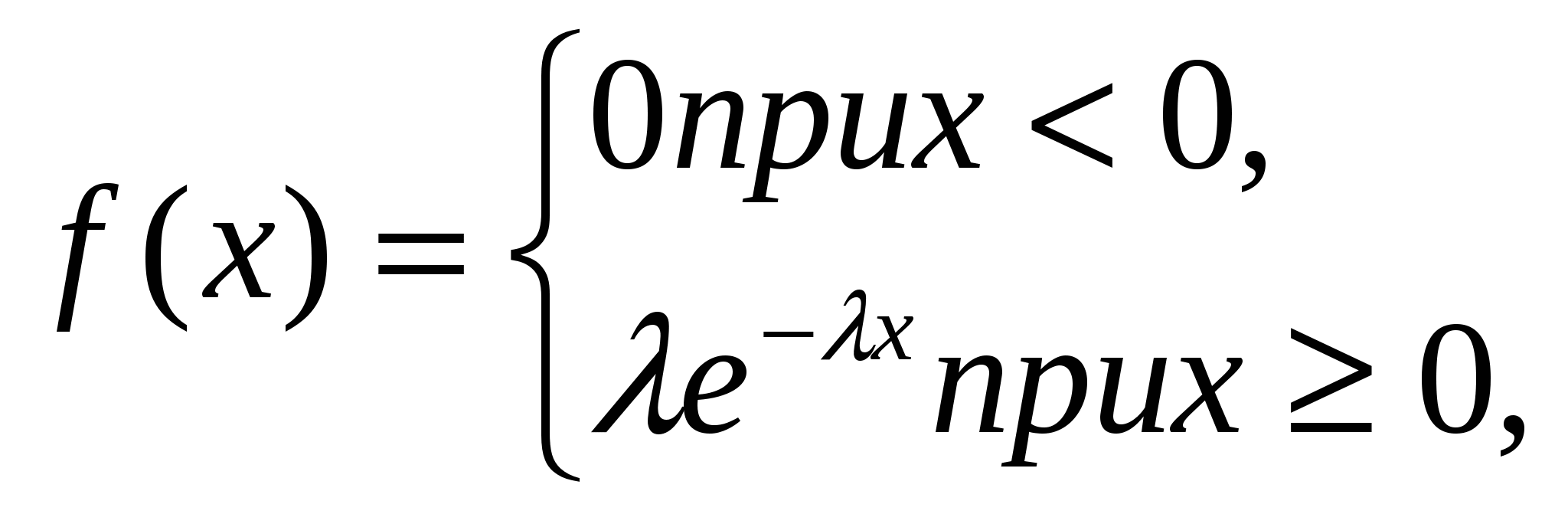



Найдем математическое ожидание (см. гл. XII, § 1):



Интегрируя по частям, получим

(*)

Таким образом, математическое ожидание показательного распределения равно обратной величине параметра ..

Найдем дисперсию (см. гл. XII, § 1):



Интегрируя по частям, получим



Следовательно,

D(X)=1/^

Найдем среднее квадратическое отклонение, для чего извлечем квадратный корень из дисперсии:

(X)=1/ (**)

Сравнивая (*) и (**), заключаем, что

М (Х) =(X)=1/

т. е. математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

Пример. Непрерывная случайная величина Xраспределена по показательному закону

f(x)=5e^-5xпри x0; f(x)=0при x<0.

Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.

Решение. По условию,  = 5. Следовательно,

М (X) = (X)= 1 / = 1 /5 = 0,2;

D(X)=1/^^

Замечание 1. Пусть на практике изучается показательно распределенная случайная величина, причем параметр  неизвестен. Если математическое ожидание также неизвестно, то находят его оценку (приближенное значение), в качестве которой принимают выборочную среднюю (см. гл. XVI, § 5). Тогда приближенное значение параметра находят с помощью равенства

^.

Замечание 2. Допустим, имеются основания предположить, что изучаемая на практике случайная величина имеет показательное распределение. Для того чтобы проверить эту гипотезу, находят оценки математического ожидания и среднего квадратического отклонения, т. е. находят выборочную среднюю и выборочное среднее квадратическое отклонение (см. гл. XVI, § 5, 9). Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой, поэтому их оценки должны различаться незначительно. Если оценки окажутся близкими одна к другой, то данные наблюдений подтверждают гипотезу о показательном распределении изучаемой величины; если же оценки различаются существенно, то гипотезу следует отвергнуть.

Показательное распределение широко применяется в приложениях, в частности в теории надежности, одним из основных понятий которой является функция надежности.
§ 4. Функция надежности
Будем называть элементом некоторое устройство независимо от того, «простое» оно или «сложное».

Пусть элемент начинает работать в момент времени t₀=0, а по истечении времени длительностью tпроисходит отказ. Обозначим через Т непрерывную случайную величину — длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее t, то, следовательно, за время длительностью tнаступит отказ.

Таким образом, функция распределения F(t)= P(T<t)определяет вероятность отказа за время длительностью t. Следовательно, вероятность безотказной работы за это же время длительностью t, т. е. вероятность противоположного события Т > t, равна

R(t)=P(T>t)=1-F(t). (*)

Функцией надежности R(t)называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t:

R(t)=P(T>t).
§ 5. Показательный закон надежности
Часто длительность времени безотказной работы момента имеет показательное распределение, функция распределения которого

F(t)=1-.

Следовательно, в силу соотношения (*) предыдущего параграфа функция надежности в случае показательного распределения времени безотказной работы элемента имеет вид

R(t) = 1 — F(t)= 1 — (1 —) =.

Показательным законом надежности называют функцию надежности, определяемую равенством

R(t)= , (*)

где — интенсивность отказов.

Как следует из определения функции надежности (см. § 4), эта формула позволяет найти вероятность безотказной работы элемента на интервале времени длительностью t, если время безотказной работы имеет, показательное, распределение.

Пример. Время безотказной работы элемента распределено по показательному закону f(t) =0,02e^-0,02t при t 0 (t — время). Найти вероятность того, что элемент проработает безотказно 100 ч.

Решение. По условию, постоянная интенсивность отказов =0,02. Воспользуемся формулой (*):

R(100) = е^-0,02*100=е^-2 = 0,13534.

Искомая вероятность того, что элемент проработает безотказно 100 ч, приближенно равна 0,14.

Замечание. Если отказы элементов в случайные моменты времени образуют простейший поток, то вероятность того, что за время длительностью tне наступит ни одного отказа (см. гл. VI, § 6),

P_t(0)= ,

что согласуется с равенством (*), поскольку  в обеих формулах имеет один и тот же смысл (постоянная интенсивность отказов).
§ 6. Характеристическое свойство показательного закона надежности
Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Объясняется это тем, что этот закон обладает следующим важным свойством: вероятность безотказной работы элемента на интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t(при заданной интенсивности отказов ).

Для доказательства свойства введем обозначения событий:

А—безотказная работа элемента на интервале (О,t₀) длительностью t₀; В—безотказная работа на интервале (t₀, t₀+t) длительностью t. Тогда АВ—безотказная работа на интервале (0, t₀+t)длительностью t_o+t.

Найдем вероятности этих событий по формуле (*) (см. § 5):

P(A)=,P(B)= ,

P(AB)= .

Найдем условную вероятность того, что элемент будет работать безотказно на интервале (t₀, t₀+t)при условии, что он уже проработал безотказно на предшествующем интервале (0, t₀)(см. гл. III, § 2):



Полученная формула не содержит t₀, а содержит только t. Это и означает, что время работы на предшествующем интервале не сказывается на величине вероятности безотказной работы на последующем интервале, а зависит только от длины последующего интервала, что и требовалось доказать.

Полученный результат можно сформулировать несколько иначе. Сравнив вероятности Р (В)= и Р_А(В)= , заключаем: условная вероятность безотказной работы элемента на интервале длительностью t, вычисленная в предположении, что элемент проработал безотказно на предшествующем интервале, равна безусловной вероятности.

Итак, в случае показательного закона надежности безотказная работа элемента «в прошлом» не сказывается на величине вероятности его безотказной работы «в ближайшем будущем».

Замечание. Можно доказать, что рассматриваемым свойством обладает только показательное распределение. Поэтому если на практике изучаемая случайная величина этим свойством обладает, то она распределена по показательному закону. Например, при допущении, что метеориты распределены равномерно в пространстве и во времени, вероятность попадания метеорита в космический корабль не зависит от того, попадали или не попадали метеориты в корабль до начала рассматриваемого интервала времени. Следовательно, случайные моменты времени попадания метеоритов в космический корабль распределены по показательному закону.
Задачи
1. Написать функцию распределения F(х)и плотность вероятности f(к)непрерывной случайной величины X, распределенной по показательному закону с параметром  = 5.

Отв. f(х)=5е^-5x при x 0; f(x) = Oпри х < 0; F(x)= 1 — e^-5x.

2. Непрерывная случайная величина Xраспределена по показательному закону: f(х) =5е^-5xпри х О, f(x)=0при х < 0. Найти вероятность того, что в результате испытания Xпопадет в интервал (0,4, 1).

Отв. Р (0,4 < X< 1)=0,13.

3. Непрерывная случайная величина Xраспределена по показательному закону f(х)=4е^-4x(х > 0). Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.

Отв. М(Х)=(Х) = 0,25; D(X) = 0,0625.

4.Время безотказной работы элемента распределено по показательному закону f(t)=0,01e^-0,01t(t>0), где t — время, ч. Найти вероятность того, что элемент проработает безотказно 100 ч.

Отв. R(100) = 0,37.