Задача 2. Седьмая математическое ожидание дискретной случайной величины

• Название: Седьмая математическое ожидание дискретной случайной величины
• Анкор: Задача 2.doc
• Дата: 27.04.2017
• Размер: 1.95 Mb.
• Имя файла: Задача 2.doc
• Тип: Глава; #5986
• страница: 5 из 7

Глава двенадцатая

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
§ 1. Числовые характеристики непрерывных случайных величин
Распространим определения числовых характеристик дискретных величин на величины непрерывные. Начнем с математического ожидания.

Пусть непрерывная случайная величина Xзадана плотностью распределения f(x). Допустим, что все возможные значения Xпринадлежат отрезку [а, b]. Разобьем этот отрезок на п частичных отрезков длиной ,,..., и выберем в каждом из них произвольную точку x_i(i = 1, 2, ..., п). Нам надо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений x_i на вероятности попадания их в интервал ; (напомним, что произведение f(х)приближенно равно вероятности попадания Xв интервал ):



Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл

Математическим ожиданием непрерывной случайной величины- X, Возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл

M(X)= (*)

Если возможные значения принадлежат всей оси Ох, то

M(X)=

Предполагается, что несобственный интеграл сходится абсолютно, т. е. существует интеграл Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к —, а верхнего—к +.

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения Xпринадлежат отрезку[a,b], то

D(X)=

если возможные значения принадлежат всей оси х, то

D(X)=

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

(X)=.

Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:

D(X)= (**)

D(X)=

Пример 1. Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения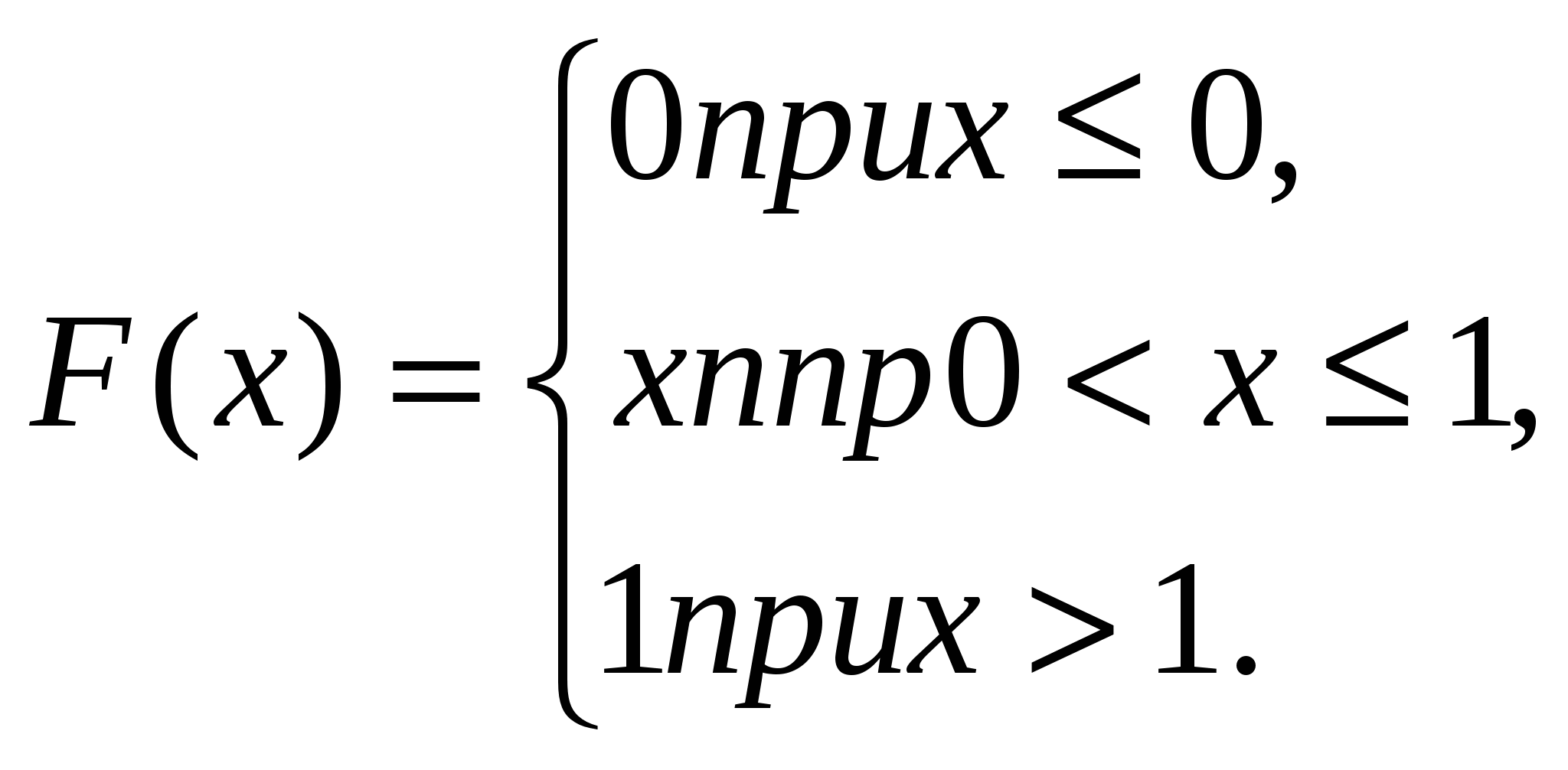



Решение. Найдем плотность распределения:


Найдем математическое ожидание по формуле (*):

M(X)=

Найдем дисперсию по формуле (**):

D(X)=

Пример 2. Найти математическое ожидание и дисперсию непрерывной случайной величины X, распределенной равномерно в интервале (а, b).

Решение. Найдем математическое ожидание Xпо формуле (*), учитывая, что плотность равномерного распределения f(x) = 1/(b — а)(см. гл. XI, § 6):

M(X)=

Выполнив элементарные выкладки, получим

M(X)=(a+b)/2

Найдем дисперсию Xпо формуле (**):

D(X)=

Выполнив элементарные выкладки, получим

D(X) = (b — a)²/12.

Замечание 3. Математическое ожидание и дисперсия случайной величины R, распределенной равномерно в интервале (0, 1), т. е. если a = 0, b=1, как следует из примера 2, соответственно равны М (R) = 1/2, D(R)=l/12. Этот же результат мы получили в примере 1 по заданной функции распределения случайной величины R.
§ 2. Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью



Мы видим, что нормальное распределение определяется двумя параметрами: а и. Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание, —среднее квадратическое отклонение нормального распределения.

а) По определению математического ожидания непрерывной случайной величины,

M(X)=

Введем новую переменную z = (x—а)/. Отсюда x=z+a, dx=dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим

M(X)=

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно a ( интеграл Пуассона ).

Итак, М(Х) = а, т. е. математическое ожидание нормального распределения равно параметру а.

б) По определению дисперсии непрерывной случайной величины, учитывая, что М(Х) = а, имеем

D(X)=

Введем новую переменную z = (x—а)/. Отсюда х—a = z, dx = dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим

D(X)=

Интегрируя по частям, положив u = z, dv=, найдем

D(X)=^

Следовательно,

(X)=.

Итак, среднее квадратическое отклонение нормального распределения равно параметру .

Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и  ( > 0).

Нормированным называют нормальное распределение с параметрами а = 0 и =1. Например, если X— нормальная величина с параметрами а и , то U =(X— а)/— нормированная нормальная величина, причем M(U)=0, (U)=1.

Плотность нормированного распределения



Эта функция табулирована (см. приложение 1).

Замечание 2. Функция F(х)общего нормального распределения (см. гл. XI, § 3)



а функция нормированного распределения


Функция F_o (x) табулирована. Легко проверить, что

F(x)=F₀((x-a)/ ).

Замечание 3. Вероятность попадания нормированной нормальной величины Xв интервал (0, х)можно найти, пользуясь функцией Лапласа Действительно (см.гл. XI, § 2),

P(0<X<x)=

Замечание 4. Учитывая, что (см. гл. XI, §4,свойство 2), и, следовательно, в силу симметрии (х)относительно нуля

, а значит, и Р (- <X < 0)=0,5,

легко получить, что

F₀(x)=0,5+(x).

Действительно,

F₀(x)=P(-<X<x)=P(-<X<0)+P(0<X<x)=0,5+(x).
§ 3. Нормальная кривая
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию

y=

методами дифференциального исчисления.

1. Очевидно, функция определена на всей оси х.



2. При всех значениях х функция принимает положительные значения, т. е. нормальная кривая расположена над осью Ох.

3. Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю: , т. е. ось Ох служит горизонтальной асимптотой графика.

4.Исследуем функцию на экстремум. Найдем первую производную:



Легко видеть, что у' = 0 при х = а, у' > 0 при х < а, у' < 0 при х> а.

Следовательно, при х = а функция имеет максимум, равный

5.Разность х—а содержится в аналитическом выражении функции в

квадрате, т. е. график функции симметричен относительно прямой х= а.

6.Исследуем функцию на точки перегиба. Найдем вторую производную:



Легко видеть, что при х = а+и х= а— вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно 1/(e)). Таким образом, точки графика (а—, 1/(e)) и (а + , 1/(e))являются точками перегиба.

На рис. 7 изображена нормальная кривая при а=1, 2
§ 4. Влияние параметров нормального распределения на форму нормальной кривой
Выясним, как влияют на форму и расположение нормальной кривой значения параметров а и .

Известно, что графики функций f(х)и f (х—а)имеют одинаковую форму; сдвинув график f(х)в положительном направлении оси х на а единиц масштаба при а >0 иливотрицательном направлении при а < 0, получим график f(х—а). Отсюда следует, что изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а подрастает, и влево, если а убывает.

По-иному обстоит дело, если изменяется параметр (среднее квадратическое отклонение). Как было указано в предыдущем параграфе, максимум дифференциальной функции нормального распределения равен 1/(). Отсюда следует, что с возрастанием  максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т. е. сжимается к оси Ох; при убывании  нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Оу.

Подчеркнем, что при любых значениях параметров а и  площадь, ограниченная нормальной кривой и осью х, остается равной единице (см. гл. XI, § 4, второе свойство плотности распределения).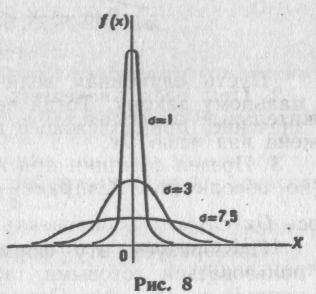



На рис. 8 изображены нормальные кривые при различных значениях  и а = 0. Чертеж наглядно иллюстрирует, как изменение параметра сказывается на форме нормальной кривой.

Заметим, что при а = О и = 1 нормальную кривую называют нормированной.
§ 5. Вероятность попадания в заданный интервал нормальной случайной величины
Уже известно, что если случайная величина Xзадана плотностью распределения f(х), то вероятность того, что Xпримет значение, принадлежащее интервалу (), такова:

P(X)=

Пусть случайная величина Xраспределена по нормальному закону. Тогда вероятность того, что Xпримет значение, принадлежащее интервалу (), равна

P(X)=

Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную z = (x—а)/. Отсюда x = z+a, dx = dz . Найдем новые пределы интегрирования. Если х= , то z=( a)/; если х =  , то z = (а)/.

Таким образом, имеем



Пользуясь функцией Лапласа



окончательно получим

(*)

Пример. Случайная величина Xраспределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность, того, что Xпримет значение, принадлежащее интервалу (10, 50).

Решение. Воспользуемся формулой (*). По условию,  =10, =50, а = 30,  =10, следовательно,

P(10<X<50)=

По таблице приложения 2 находим Ф (2) = 0,4772. Отсюда искомая вероятность

Р(10< X< 50) =2*0,4772 = 0,9544.