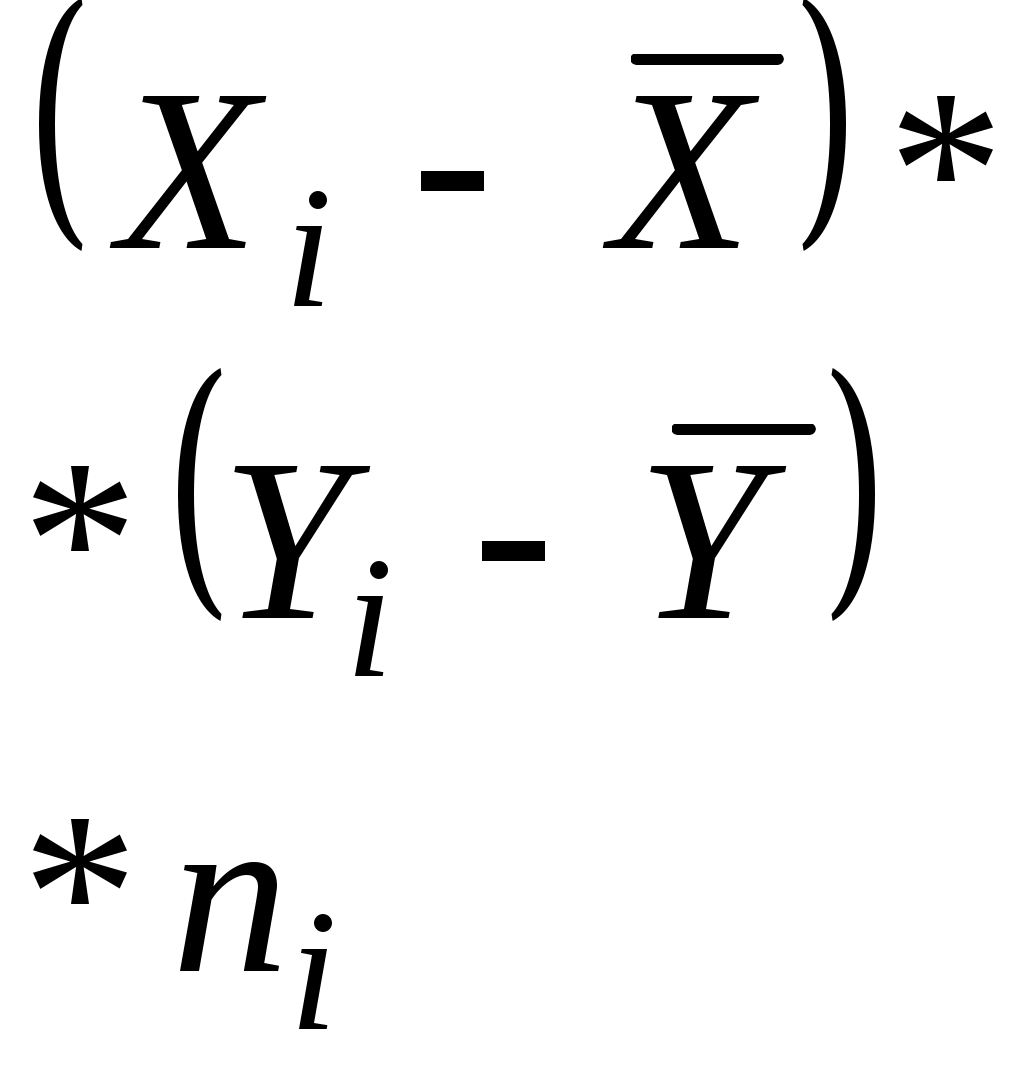Методичка к индивидуальному заданию. Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения

• Название: Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения
• Дата: 05.04.2022
• Размер: 1.66 Mb.
• Имя файла: Методичка к индивидуальному заданию.doc
• Тип: Документы; #444146
• страница: 13 из 13

РАСПРЕДЕЛЕНИЯ

После установления согласия теоретического и эмпирического распределений следует уточнить достоверность оценок параметров теоретического распределения путем определения доверительных интервалов. Последние могут быть точно определены только в случае известных законов распределения. Методику определения доверительных интервалов для различных законов распределения можно найти в следующей литературе:

- для логарифмически нормального [6,с.55; 15,с.179);

- для экспоненциального [3,с.217; 15,с.165];

- для Вейбулла [15,с.176];

- для гамма [15,с.178].

13. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Для характеристики тесноты связи между двумя случайными величинами, относящимися к двумерной выборке, в статистике используется эмпирический коэффициент корреляции. Он вычисляется при достаточно большом объеме выборки (n50) по формуле



где - эмпирический корреляционный момент.

Для определения коэффициента корреляции должна быть проведена обработка эмпирических данных x и y, полученных в результате исследования выборки, и определены выборочные средние и , а также выборочные среднеквадратические отклонения S_X и S_Y. Полученное значение r является точечной состоятельной оценкой коэффициента корреляции генеральной совокупности - .

Средняя квадратическая ошибка приближенно равна

.

Следовательно, можно приближенно считать, что лежит в пределах

_.

При оценке надежности коэффициента корреляции важно убедиться в том, что абсолютная величина коэффициента корреляции превышает вычисленную ошибку по крайней мере в 3 раза, т.е. [2]. Более полные сведения по оценке точности коэффициента корреляции можно найти в [2, с.241; 6,с.113; 9,с.359; 10,с.142; 11,с.294; 20,с.203].

Определение коэффициента корреляции проводится по дискретному ряду с помощью таблицы следующего вида:

18,0	0,5	3	54,0	1,5	-6	-0,2	108	0,12	3,6

Где

; ; ;

; ;

.

Для упрощения вычислений можно выбрать новое начало отсчета и масштаб измерения величин X и Y [6,с.110].

14. ЗАКЛЮЧЕНИЕ
Приведенный объем статистической обработки опытных данных достаточен для ознакомления с этой процедурой. После освоения предложенного минимума можно переходить к более сложным случаям и методам, к использованию ЭВМ для обработки результатов наблюдений, экспериментов и т. п. Это позволяет осуществить та многочисленная литература, которая издана по рассматриваемому вопросу.
ЛИТЕРАТУРА

1. 
   СТ.СЭВ 1190-78. Правила проверки согласия опытного распределения с теоретическим.
   
2. 
   Длин А. М. Математическая статистика в технике.- М.: Советская наука, 1958.
   
3. 
   Шор Я. Б. Статистические методы анализа и контроля качества и надежности.- М.: Сов. радио, 1962.
   
4. 
   Демаков И. П. Методы статистической проверки однородности информации об эксплуатационной надежности изделий. - Л.: ЛДНТП, 1968.
   
5. 
   Колкер Я. Д. Математический анализ точности механической обработки деталей. - Киев: Техника, 1976.
   
6. 
   Румшиский Л. З. Математическая обработка результатов эксперимента. - М.: Наука, 1971.
   
7. 
   Янко Я. Математико-статистические таблицы. - М.: Статиздат, 1961.
   
8. 
   Кутай А. К., Файнштейн Г. З. Об оценке резко выделяющихся наблюдений.// - Измерительная техника.- 1967.- N1.
   
9. 
   Митропольский А. К. Техника статистических вычислений. - М.: Наука, 1971.
   
10. 
    Герасимович А. И., Матвеева Я. И. Математическая статистика. - Минск: Вышейшая школа, 1978.
    
11. 
    Смирнов Н. В., Дунин-Барковский И. В. Краткий курс математической статистики для технических приложений. - М.: Физматгиз, 1959.
    
12. 
    Ван-дер-Варден Б. Л. Математическая статистика. - М.: ИЛ, 1960.
    
13. 
    Гетопанов В. Н., Алешин Ю. Н. Методы равночастотных интервалов при построении гистограмм.// - Надежность и контроль качества.-1973.- N1.- C.23-26.
    
14. 
    СТ.СЭВ 3542-82. Прикладная статистика. Правила построения и применения вероятностных сеток.
    
15. 
    Шор Я. Б., Кузьмин Ф. Н. Таблицы для анализа и контроля надежности. - М.: Сов. радио, 1968.
    
16. 
    Сборник задач по теории надежности./ Под ред. А. М. Половко и И. М. Маликова. - М.: Сов. радио, 1973.
    
17. 
    Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров)/ Пер. с англ.- М.: Наука, 1974.
    
18. 
    Вентцель Е. С. Теория вероятностей. - М.: Наука, 1964.
    
19. 
    Левин Б. Р. Теоретические основы статистической радиотехники. Изд. 2-е. Книга 2-я.- М.: Сов. радио, 1975.
    
20. 
    Справочник по надежности./ Под ред. Б. Р. Левина./ Пер. с англ. Т.1.-М.: Мир, 1969.
    
21. 
    Заездный А. М. Основы расчетов по статистической радиотехнике. - М.: Связь, 1969.
    
22. 
    Шишонок Н. А. и др. Основы теории надежности и эксплуатации радиоэлектронной техники.- М.: Сов.радио, 1964.
    
23. 
    Справочник по теории вероятностей и математической статистике./ Под ред. В. С. Королюка. - Киев: Наукова думка, 1978.
    
24. 
    Ллойд Д. К., Липов М. Надежность: организация исследования, методы, математический аппарат./ Пер. с англ. - М.: Сов. радио, 1964.
    
25. 
    Крамер Г. Математические методы статистики. - М.: Мир, 1975.
    
26. 
    Дружинин Г. В. Надежность автоматизированных систем. - М.: Энергия, 1977.
    
27. 
    Надежность электронных элементов и систем./ Под ред. Х. Шнайдера./ Пер. с нем. - М.: Мир, 1977.
    
28. 
    Левин Б. Р. Теоретические основы статистической радиотехники. Изд. 2-е. Книга 3-я.- М.: Сов. радио, 1976.
    
29. 
    Головач А. В. и др. Критерии математической статистики в экономических исследованиях. - М.: Статистика, 1973.
    
30. 
    Кузьмин Г. С. Метод ускоренного вычисления критериев согласия при анализе законов распределения.// - Стандарты и качество, 1975.- N 5.- C. 84-85.
    
31. 
    Кассандрова О. Н., Лебедев В. В. Обработка результатов наблюдений: Учебное пособие для вузов. - М.: Наука, 1970.
    
32. 
    Иоффе А. Я. и др. Краткий справочник по вероятностным и статистическим расчетам. - Л.: ЛВИКА им. А. Ф. Можайского, 1969.
    
33. 
    Груничев А. С., Михайлов А. И., Шор Я. Б. Таблицы для расчетов надежности при распределении Вейбулла. - М.: Изд. стандартов, 1974.- 63 с.
    
34. 
    Креденцер Б. П. и др. Решение задач надежности и эксплуатации на универсальных ЭЦВМ.- М.: Сов. радио, 1967. - 400 с.
    
35. 
    Северцев Н. А. Надежность сложных систем в эксплуатации и отработке: Учебн. пособие для вузов. - М.: Высш. шк., 1989.- 432с.
    
36. 
    Кульбак С. Теория информации и статистика. - М.: Наука, 1967.
    
37. 
    Кундорф Г. Введение в теорию оценивания по группированным и частично группированным выборкам. - М.: Наука, 1966.
    
38. 
    Алешин А. В. Методика подбора функций распределения для построения математических моделей отклонения параметров РЭА. В сб. Конструкторско-технологические аспекты проектирования РЭА.- М., МИРЭА, 1981, - с. 53-62.
    
39. 
    Дьерфель К. Статистика в аналитической химии. - М.: Мир, 1969. - 247 с.
    

С о д е р ж а н и е

Предисловие . . . . . . . . . . . . . . . . . . . . . . . 3

1.Введение. . . . . . . . . . . . . . . . . . . . . . . . . 3

2.Порядок статистической обработки опытных данных . . . . . 4

3.Формы представления первичных данных . . . . . . . . . . 5

4.Исключение грубых ошибок наблюдений . . . . . . . . . . . 7

5.Построение рядов распределения. . . . . . . . . . . . . .11

6.Построение эмпирических кривых распределения . . . . . .18

7.Определение доверительных границ . . . . . . . . . . . .21

8.Выбор теоретического закона распределения . . . . . . . .24

9.Определение числовых характеристик эмпирического

распределения . . . . . . . . . . . . . . . . . . . . . .27

9.1.Вычисление статистик по интервальному ряду

распределения . . . . . . . . . . . . . . . . . . . .28

9.2.Вычисление статистик по способу “условного нуля”

(способ произведений) для интервального ряда . . . .30

9.3.Применение статистик для выбора закона распределения 33

9.4.Вычисление доверительных интервалов для числовых

характеристик . . . . . . . . . . . . . . . . . . . .35

10.Расчет теоретических кривых распределений и оценки

их параметров . . . . . . . . . . . . . . . . . . . . . .39

10.1.Нормальное распределение . . . . . . . . . . . . . .41

10.2.Распределения, отличные от нормального . . . . . . .48

11.Проверка правильности выбора теоретического закона

распределения по критериям согласия . . . . . . . . . . .55

11.1.Критерий Колмогорова . . . . . . . . . . . . . . . .55

11.2.Критерий Пирсона(ХИ-квадрат) . . . . . . . . . . . .58

11.3.Критерий Мизеса(омега-квадрат) . . . . . . . . . . .61

12.Уточнение достоверности оценок параметров распределения .61

13.Определение коэффициента корреляции . . . . . . . . . . .62

14.Заключение . . . . . . . . . . . . . . . . . . . . . . . 63

Литература . . . . . . . . . . . . . . . . . . . . . . . 64