Методичка к индивидуальному заданию. Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения
 Скачать 1.66 Mb.
|
|
После визуальной оценки согласия по вероятностной бумаге эмпирического распределения с выбранным теоретическим распределением необходимо проверить соответствие между ними по критериям согласия.  Рисунок 6 Недостатком графического способа выбора закона распределения является то, что часто приходится перебирать несколько типов вероятностных бумаг, прежде чем будет найден подходящий закон. Поэтому перед использованием графического способа следовало бы иметь какие-то рекомендации о последовательности применения соответствующих типов вероятностных бумаг, с какого закона распределения начинать подбор. Например, если исследуется надежность изделий, то применять тот или иной тип вероятностной бумаги следует по степени распространенности законов распределения отказов в следующем порядке [16]: экспоненциальный, усеченный нормальный, логарифмически нормальный, Вейбулла, гамма. Если нет никаких рекомендаций, то начинать подбор следует с нормального закона как наиболее распространенного. Здесь следует отметить, что в теории надежности обычно исследуется вероятность безотказной работы. Поэтому на вероятностную бумагу наносят не накопленные эмпирические частоты, представляющие эмпирическую функцию распределения, тождественную вероятности отказа, а разности  или  , представляющие функцию вероятности безотказной работы.Пятый и шестой способы, требующие предварительного вычисления различных моментов случайной величины по ряду распределения, будут рассмотрены ниже. Для большинства случаев можно рекомендовать следующий порядок выбора теоретического закона распределения: предварительный выбор на основании имеющихся рекомендаций по предыдущим опытам или с помощью любого из первых трех способов, уточнение выбранного закона с помощью графического способа, а если вычислены моменты, то с помощью пятого и шестого способов, и окончательная проверка соответствия теоретического распределения эмпирическому с помощью критериев согласия. 9. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ ХАРАКТЕРИСТИК ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ Эмпирические распределения, как и теоретические, характеризуются числовыми характеристиками, которые являются моментами распределения различных порядков. Для эмпирического распределения это будут выборочные моменты. Они характеризуют статистические свойства выборки и называются также статистиками. К числовым характеристикам одномерных распределений относятся [17]: квантили; характеристики положения (центр распределения – математическое ожидание или среднее значение, медиана, мода); характеристики рассеяния (дисперсия, среднее квадратическое отклонение, коэффициент вариации, среднее абсолютное отклонение, интервальная широта, размах, полуширота); характеристики асимметрии и эксцесса (коэффициент асимметрии, коэффициент эксцесса, пирсоновская мера асимметрии). Асимметрия указывает на характер скошенности функции f(x). При A=0 кривая симметрична, при A>0 вытянута правая, а при А<0 левая спадающая часть кривой. Искажения формы оцениваются относительно формы нормального распределения. Эксцесс является показателем "сгруппированности" случайных величин относительно среднего значения и характеризует степень заостренности пика кривой (относительно кривой нормального распределения). Числовые характеристики выборочного распределения являются оценками параметров теоретического распределения и поэтому к ним предъявляются следующие требования: - несмещенность; - состоятельность; - эффективность. Несмещенность означает, что оценка не должна преувеличивать или преуменьшать значение параметра, т.е. в наблюдениях отсутствуют систематические погрешности. Состоятельность означает, что с увеличением объема информации оценка должна приближаться к величине параметра. Эффективность означает, что данная оценка является наиболее точной, т.е. имеет минимальную дисперсию или наименьшее рассеяние, чем любые другие несмещенные оценки, найденные из тех же самых данных другими способами. Однако одних этих критериев недостаточно. Для практических технических ситуаций необходимо иметь рабочие правила, позволяющие получить оценки с таким количеством полезных свойств насколько это возможно. Такими правилами являются: - метод максимального правдоподобия; - метод наименьших квадратов. Ниже рассматриваются точечные оценки параметров распределения. Числовые характеристики выборочного распределения (статистики) могут вычисляться как для дискретного, так и для интервального рядов распределения по известным формулам для моментов. Существует несколько способов определения статистик: по ряду распределения; способ произведений или "условного нуля"; способ сумм [9], который удобен при большом числе интервалов или разрядов в ряде распределения, и т.п. Рассмотрим некоторые способы на примере. 9.1 Вычисление статистик по интервальному ряду распределения Воспользуемся табл.4. Среднее значение  вычисляется по формуле:  Эмпирическое среднее квадратическое отклонение S находится через эмпирическую дисперсию, которая определяется по следующему выражению:   .Откуда  .При небольшом объеме выборки из-за того, что отличается от математического ожидания, оценка S получается смещенной. Несмещенная оценка среднего квадратического отклонения для малой выборки вычисляется по формуле .Для нашего примера в этом случае разницы практически не будет, так как (отличие на  ). При n=50 отличие в результатах расчета по обеим формулам составляет порядка  . Поэтому формула для несмещенной оценки применяется при объеме выборки от единиц до двух-трех десятков (n30). Для вычисления медианы воспользуемся формулой, приведенной в [2]: ,где  - начало медианного интервала; - последний член кумулятивного ряда, меньший или равный n/2; - частота медианного интервала.Для нашего примера =825, h=10, n/2=200/2=100, Hi=55, =47.Тогда  .Моду вычислим по следующему выражению [2]: 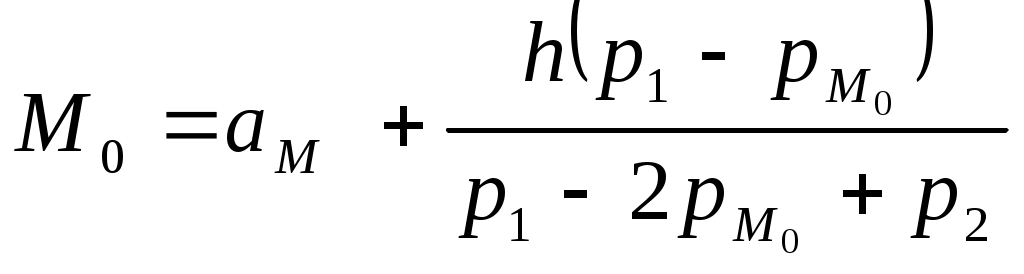 ,где  - начало модального интервала; - частость модального интервала; и  - частости соседних с модальным интервалов.Для нашего примера =825, h=10, =0,170, =0,235, =0,220.Тогда  .Меру асимметрии А и коэффициент эксцесса Е (или просто асимметрию и эксцесс) вычисляют через центральные моменты третьего  и четвертого  порядков по формулам и  ,где  ,  - эмпирические моменты.Коэффициент вариации определяется выражением  или  .Для рассматриваемого примера  или  .9.2. Вычисление статистик по способу “условного нуля” (способ произведений) для интервального ряда Вычисление моментов может быть существенно упрощено, если учитывать наличие определенных соотношений между различными видами моментов. Способ заключается в выборе нового начала отсчета, переходе от действительных значений случайной величины (вариантов) к условным вариантам, вычислении условных начальных и центральных моментов и определении через них числовых характеристик эмпирического распределения. Новое начало отсчета (ложный или условный нуль)  берется в середине среднего по порядку интервала или интервала с наибольшей частотой. Условные варианты определяются по соотношению .Условные варианты являются целыми числами, так как разность берется между представителями интервалов, которые равны значениям случайной величины в серединах интервалов. Для удобства вычислений составляется табл. 7. Выбираем  . Из табл.4 берем значения  и  . Начальные моменты k-го порядка определяются по формуле ,в соответствии с которой условные начальные моменты будут равны  ; ; ; .В скобках указаны номера столбцов табл. 7. Условно-условный момент четвертого порядка  .Проверку правильности вычислений проводят по формуле   .Для дальнейших расчетов необходимо найти  ,  ,  : ,  ,  .Затем определяются условные центральные моменты:  ; ;  .Правильность вычислений проверяется по формуле   .Для более точных вычислений моментов следует учитывать поправки Шеппарда [2,9]. |