Методичка к индивидуальному заданию. Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
Следует отметить, что это предварительный выбор количества интервалов, который в дальнейшем иногда подлежит уточнению при построении эмпирической кривой распределения для устранения зигзагообразности, провалов и т.п.После выбора количества интервалов определяют ширину интервала h путем деления размаха варьирования R, равного разности между наибольшим и наименьшим значениями признака, на количество интервалов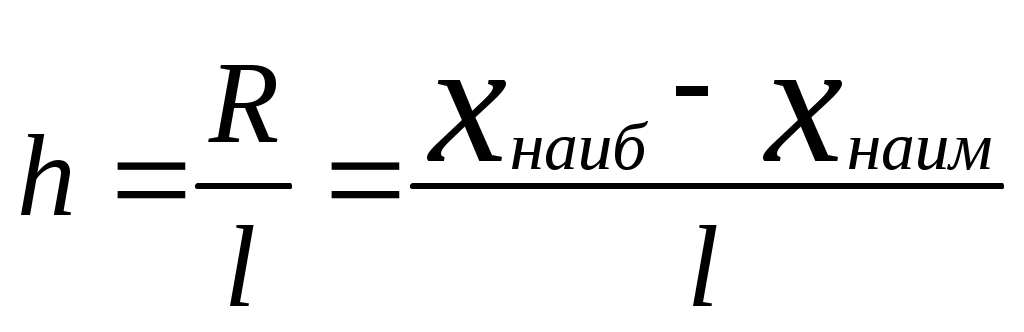 . .Полученное число округляется до ближайшего из предпочтительного ряда. Рекомендуется выбирать значения h равными 1, 2, 3, 5, 7, 10, 15 или числу, кратному 5 [5]. Там же рекомендуется выбирать h примерно в два раза больше, чем цена деления измерительного прибора, что не всегда возможно, так как при этом уменьшается количество интервалов. Но в любом случае ширина интервала не должна быть меньше цены деления измерительного прибора [2]. Для ширины интервала нужно всегда выбирать удобное число и не записывать ее с "дикой" точностью, благодаря большому числу разрядов, например в калькуляторах, применяемых при расчетах. И еще некоторые рекомендации для построения интервального ряда распределения. Границы интервалов не должны совпадать с измеренными значениями [2]. Если это получилось, то следует расширить размах варьирования за счет некоторого смещения его нижнего предела влево, а его верхнего предела - вправо. Например, если ширина интервала равна цене деления измерительного прибора, то следует величину смещения взять равной половине ширины интервала. Тогда все данные будут располагаться в серединах интервалов. Если при смещении крайних границ не удается избежать совпадения измеренных значений с границами промежуточных интервалов, то в таких случаях следует условиться к какому из интервалов, левому или правому, отнести эти значения. Довольно часто рекомендуется значения, совпадающие с границами интервалов, делить пополам, т.е. половину таких значений относить к левому интервалу, а половину - к правому. Чтобы не иметь дело с дробями при нечетном количестве значений, совпадающих с границей интервалов, следует условиться, к какому интервалу, левому или правому, будет отнесено лишнее значение. Можно в этом случае также все количество значений умножить на два. Это не внесет ошибки, так как вероятность попасть в каждый из интервалов не изменится. Следует заметить, что от способа распределения значений, совпадающих с промежуточными границами, по интервалам несколько зависят результаты расчетов. Рассмотрим на примере наиболее часто используемый способ построения интервального ряда распределения по крайним значениям признака. Обычно используется следующий порядок построения. 1. По табл.1 или вариационному ряду находим наибольшее и наименьшее значения параметра 2. Определяем размах варьирования 3. Выбираем число интервалов В нашем случае удобно выбрать 4. Определяем ширину интервала 5. Чтобы крайние границы размаха варьирования не совпадали с измеренными значениями, отступаем на половину ширины интервала вправо и влево соответственно от верхнего и нижнего пределов варьирования. Получаем новые границы. При этом границы первого интервала будут 795 и 805, второго – 805 и 815 и т.д. Теперь интервалов стало Как видно из табл.1, нам не удалось избежать совпадения измеренных значений с промежуточными границами интервалов. Поэтому условимся относить те значения, которые попадают на границы интервалов, к левому интервалу. Пример построения интервального ряда распределения приведен в табл. 3. Таблица 3
|
