Методичка к индивидуальному заданию. Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
Если преобразовать неравенство к виду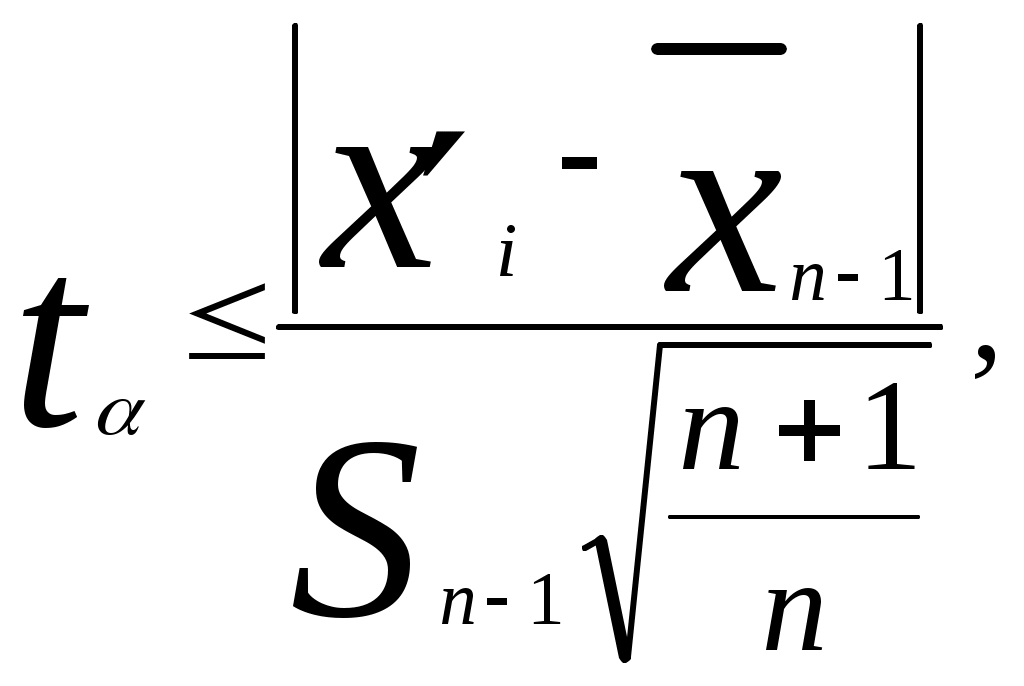 то оно напоминает метод Романовского [5], при котором оценивается 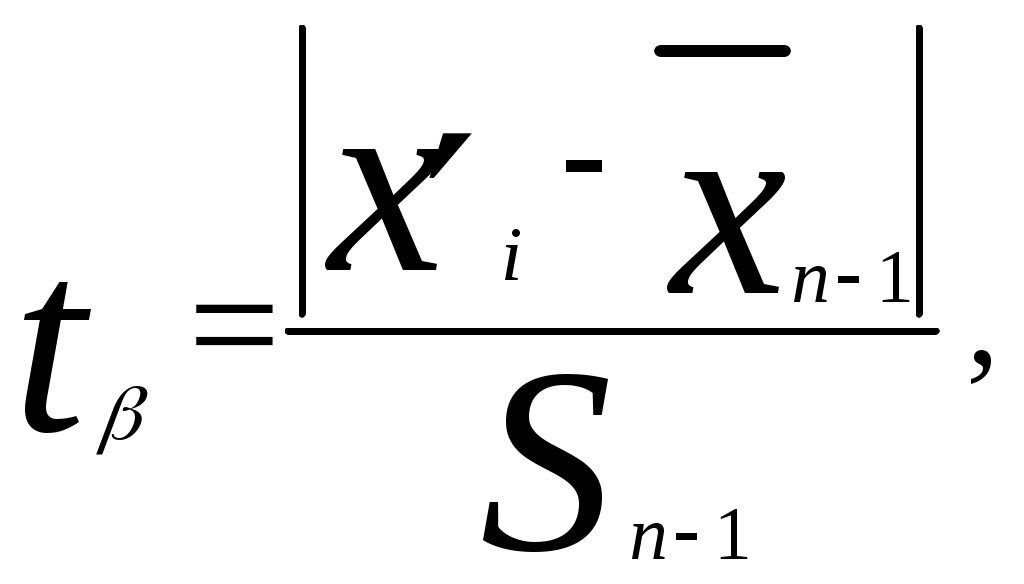 где В рассмотренных двух методах не приходится пересчитывать среднее значение Во всех остальных методах (кроме упрощенных критериев) приходится после исключения грубой ошибки снова определять значения Критерий типа r [4] определяет величину 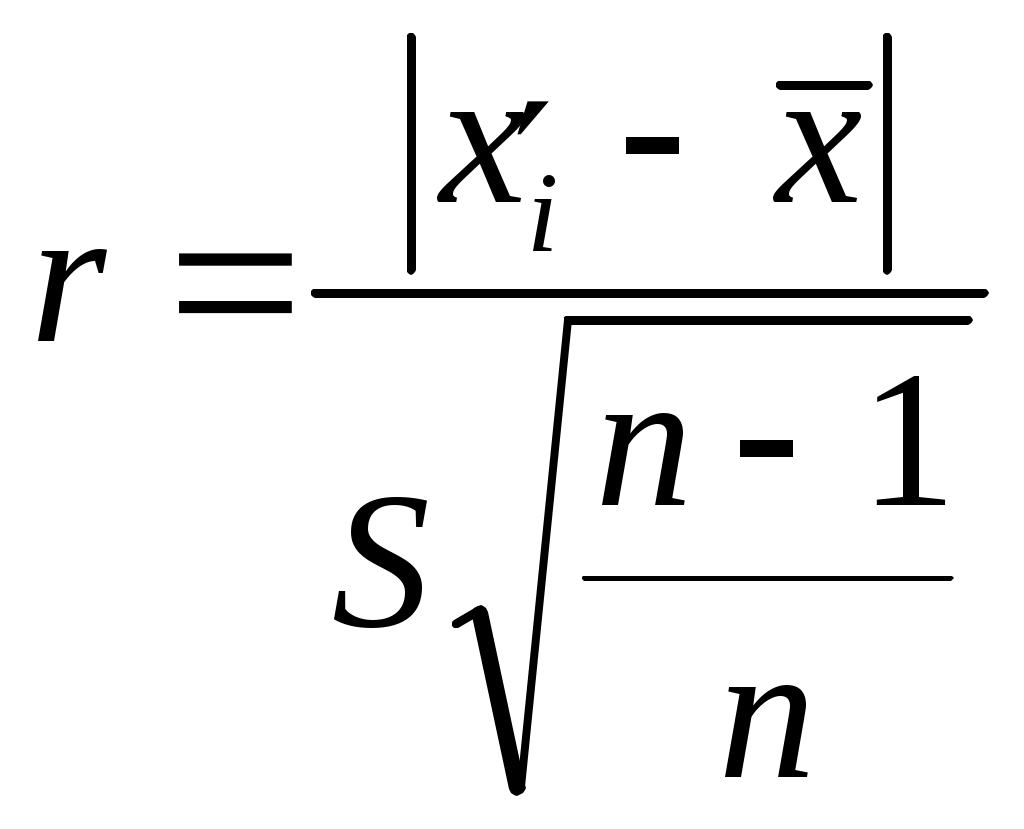 , ,где Если преобразовать знаменатель этого критерия, то мы получимгде Полученное выражение совпадает с методом Грэббса [5]В методе исключения грубой ошибки при известной [6] определяется величина 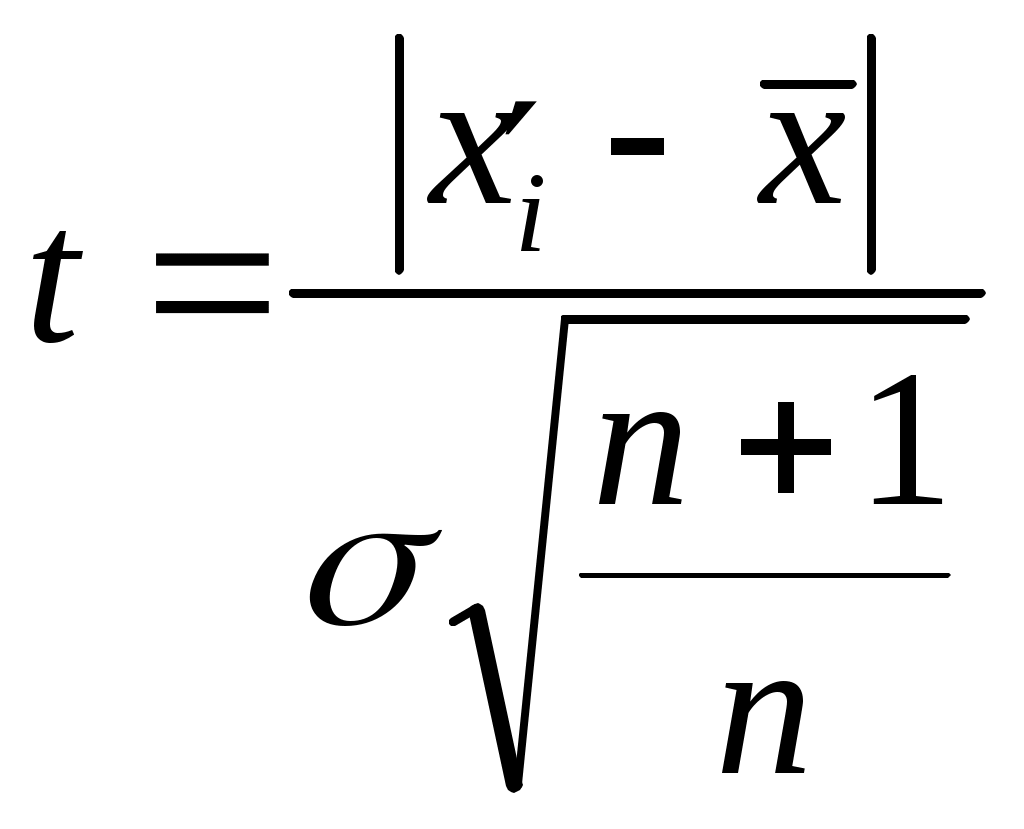 , ,а в методе оценки анормальности результатов измерений при известной генеральной дисперсии [3] определяется величина В методе исключения грубых ошибок при неизвестной [6] определяется величина то есть та же, что и в методе оценки анормальности результатов измерений при неизвестной генеральной дисперсии [3]. Таким образом, последний метод отличается от критерия типа r и метода Грэббса только способом определения среднего квадратического отклонения (несмещенная оценка). Метод упрощенных критериев [4] предполагает определение отношения отклонения экстремального члена выборки к ее размаху. Определяются величины поскольку экстремальные члены могут лежать слева и (или) справа от основной части выборки. Как указано выше, в этом методе не приходится определять Для случая оценки резко выделяющегося члена выборки при справедливости показательного распределения используется критерий Р. Фишера [4]. Таблицы для сравнения полученных критериев с их критическими значениями приведены в указанной в тексте литературе. А для метода Грэббса можно использовать [8]. Существует также критерий Ирвина [4,5], о котором не указывается, что он применим при определенном распределении. Метод или критерий Ирвина основан на оценке разности двух наибольших или наименьших членов выборки. Определяется величина , равная 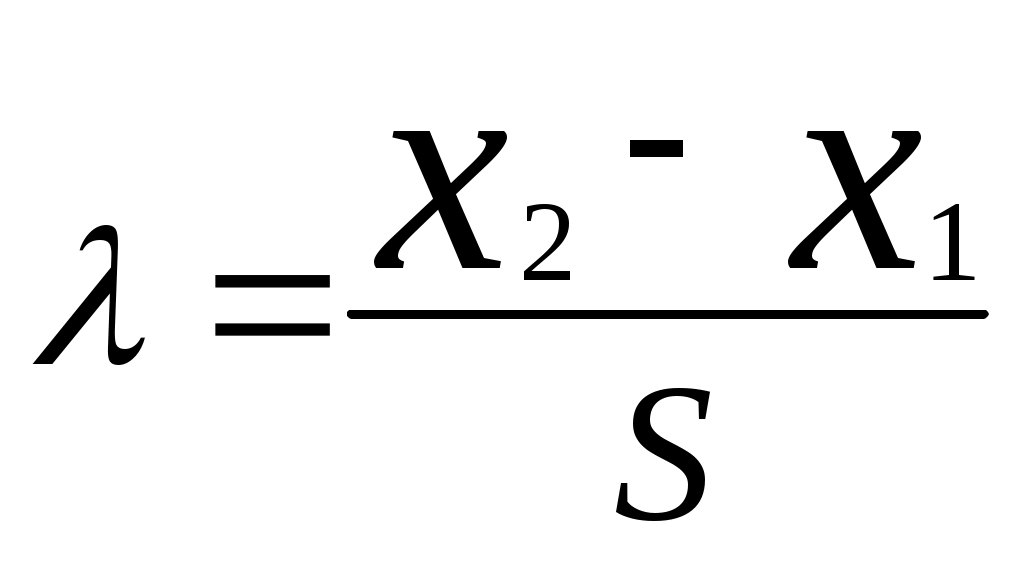 или или 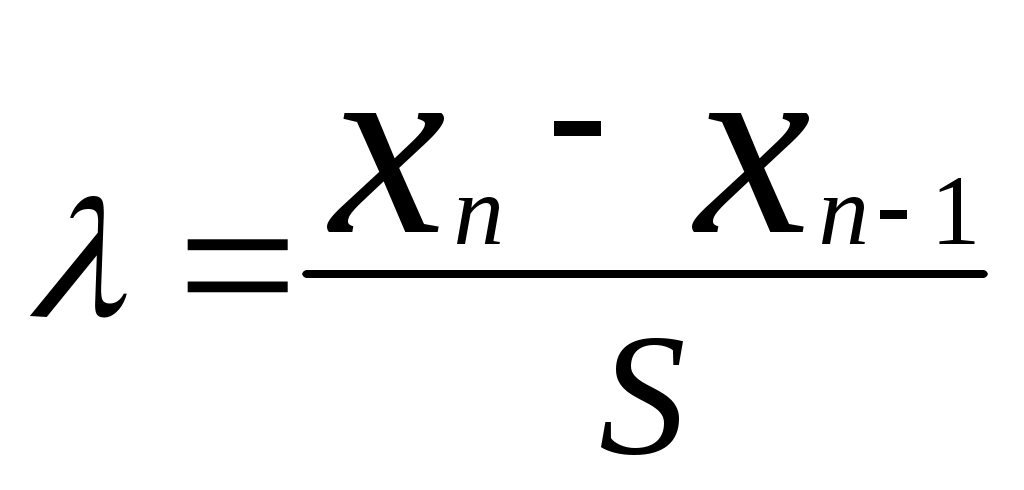 , ,в зависимости от того, с какой стороны выборки расположен резко выделяющийся член выборки. По приведенной таблице (или таблице [7]) в зависимости от объема выборки n при уровне значимости =0,95 находят критическое значение
Если оказывается, что рассчитанная 5. ПОСТРОЕНИЕ РЯДОВ РАСПРЕДЕЛЕНИЯ Рядом распределения называется совокупность значений признака вместе с соответствующими им частотами или частостями. Ряд распределения записывается в виде таблицы, в которой в определенном порядке перечислены возможные значения случайной величины (признака) и соответствующие им частоты (или) и частости. Иногда такие ряды называют статистическими. В ряде распределения возможные значения случайной величины могут быть представлены или в виде дискретных значений или в виде интервалов (разрядов). Они образуют соответственно дискретный и интервальный ряды (сгруппированный и интервальный статистические ряды [10]). Выбор того или иного ряда определяется выбранным методом для нахождения закона распределения и его числовых характеристик и применяемым критерием согласия. Построение ряда распределения представляет собой первичную обработку статистических данных. Он строится по частотам или частостям (статистическим вероятностям) на основе простого статистического (табл.1) или вариационного рядов. В табл. 2 приведен пример построения дискретного ряда. В такой ряд записываются те значения параметра, которые получаются при измерениях, и подсчитывается их количество (частоты). По частотам могут быть вычислены частости Дискретный ряд распределения используется при применении графического метода и критериев согласия Колмогорова и Мизеса Таблица 2
При построении интервального ряда наибольшую трудность составляет выбор количества интервалов, которое определяет ширину интервала. Количество интервалов оказывает влияние на форму эмпирической кривой распределения, которая представляется графически, на объем вычислительных работ, на показатели асимметрии и эксцесса, на выбор теоретического закона распределения, который описывает исследуемую совокупность случайных величин, а также на результат оценки согласия по критериям Колмогорова и Пирсона [12]. Это объясняется тем, что при большом числе интервалов эмпирическая кривая может оказаться многовершинной, иметь нехарактерные для нее случайные колебания, так как при малой ширине интервалов в него попадает мало данных. Наоборот, при малом число интервалов могут быть потеряны характерные особенности распределения. Следовательно, количество интервалов надо выбирать таким, чтобы оно способствовало выявлению основных черт распределения и сглаживанию случайных колебаний. При этом все интервалы могут иметь одинаковую (равноширотные интервалы) или разную ширину (разноширотные интервалы). Интервалы разной ширины используются в том случае, когда имеет место крайне неравномерное распределение случайных величин. Тогда в области наибольшей плотности распределения берутся интервалы более узкие, чем в области малой плотности. Часто более широкие интервалы приходится брать на краях распределения, так как требуется, чтобы количество частот в интервале было не менее пяти. Но трудности в расчете характеристик, которые при этом возникают, приводят к тому, что обычно берутся интервалы одинаковой ширины (равноширотные интервалы). При выборе числа ин тервалов необходимо иметь в виду, что ширина интервала должна быть не менее чем в два раза больше погрешности измерения параметра. В работах [36, 37] показано, что группировка данных в общем случае приводит к потере информации. В [36] установлено, что для каждого закона распределения существует оптимальное число интервалов гистограммы, при котором вид гистограммы оказывается наиболее близким к действительному виду кривой плотности распределения. Но поскольку, приступая к обработке опытных данных, мы, как правило, не знаем закона распределения исследуемой величины, то для выбора количества интервалов приходится пользоваться ниже- приведенными рекомендациями, которые весьма различны. Так, в [2] указывается, что довольно часто число интервалов берут равным 7, 9 или 11 в зависимости от числа наблюдений и точности измерений. В [9] рекомендуется число интервалов принимать равным 12 с отклонением от него на 2-3 единицы в ту или иную стороны, т.е. от 9 до 15. В [10] указывается, что количество интервалов берут произвольно, обычно не меньше 5 и не более 15. В [11] рекомендуется брать число интервалов от 10 до 20 при количестве наблюдений порядка 200-300. Таким образом, количество интервалов выбирается в пределах от 5 до 20. Естественно, что чем больше данных наблюдений, тем больше можно брать интервалов. Оптимальное количество интервалов выбирается по правилу Старджесса где n - количество наблюдений (объем выборки). Но в [5] указывается, что такое количество интервалов берется только при объеме выборки n100. А при объеме выборки n>100 следует количество интервалов определять по формуле Можно пользоваться для выборки количества интервалов следующей таблицей, приведенной в [5]:
Однако в стандартах требуется, чтобы количество интервалов выбиралось в следующих рекомендованных пределах
|
