Методичка к индивидуальному заданию. Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения
 Скачать 1.66 Mb.
|
|
Доверительные границы для неизвестной теоретической функции распределения построены на рис.5.  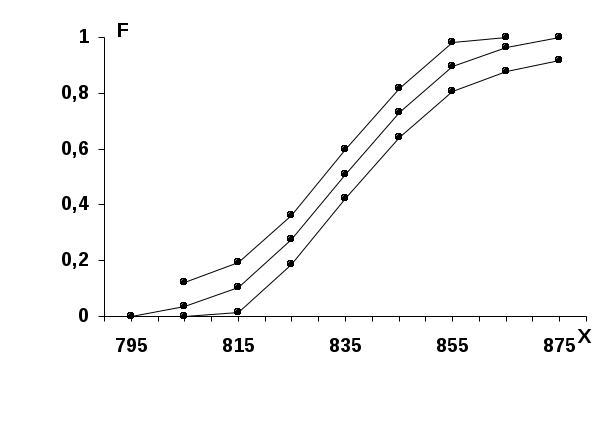 Рис. 5 8. ВЫБОР ТЕОРЕТИЧЕСКОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ Одной из главных задач статистической обработки опытных данных является подбор теоретического закона распределения для исследуемой случайной величины. Эту задачу редко удается осуществить с первой попытки и, как правило, приходится перебрать несколько законов распределения, прежде чем удастся отыскать тот, который имеет хорошее согласие с эмпирическим распределением. Это объясняется тем, что нет обоснованных правил выбора теоретического закона распределения. Предварительный выбор теоретического закона распределения может производиться: - на основании данных о механизме образования случайной величины или физического анализа задачи; - путем качественного анализа распределения частот или частостей в ряде распределения; - путем качественного анализа вида гистограммы или полигона; - графическим способом (с помощью вероятностных бумаг); - по величине эмпирического коэффициента вариации; - по коэффициентам асимметрии и эксцесса. Первый способ применяется в том случае, если заранее известен механизм образования случайной величины. Например, при одинаковом влиянии большого числа различных факторов случайная величина подчиняется нормальному закону; при наличии доминирующего фактора может быть справедливым иной закон распределения (Максвелла или другой) и т.д. Второй способ используется, когда построен интервальный ряд распределения, и он сравнительно легко поддается качественному анализу. Так, рассматривая ряд, представленный в табл. 3 и 4, нетрудно заметить, что частоты и частости распределены приблизительно симметрично относительно середины размаха варьирования и их изменение приблизительно одинаково, но не равномерно, по обе стороны от середины. Следовательно, распределение, по-видимому, подчиняется нормальному закону. Третий способ, однако, лучше подходит для качественного анализа распределения. Нетрудно построить полигон или гистограмму, если построен интервальный ряд. А по их виду проще подбирать теоретический закон распределения. Из рис. 1 или 3 следует, что исследуемое распределение, по-видимому, близко к нормальному. Четвертый способ - графический - состоит в том, что для определения закона распределения применяются специальные бумаги, называемые вероятностными (или вероятностные сетки). На таких бумагах по координатным осям наносятся соответствующие шкалы, рассчитанные так, что в этих координатах график функции распределения представляет прямую линию. Для разных законов распределения существуют свои типы вероятностных бумаг. Правила и таблицы для построения и применения таких бумаг и их образцы можно найти в [14,15,16,20]. Для определения закона распределения по вероятностной бумаге необходимо сначала построить дискретный ряд распределения, если объем выборки n50, и интервальный ряд с количеством интервалов  при n>50[14]. Количество частот в интервале должно быть не менее 5 (ni5).Рекомендации по выбору количества интервалов приведены в разделе 5. В обоих случаях должны быть подсчитаны накопленные частости, которые и представляют эмпирическую функцию распределения. Значения  наносятся на выбранный тип вероятностной бумаги и полученные экспериментальные точки аппроксимируются прямой линией. Если это удается и опытные точки располагаются близко к прямой, то это свидетельствует в первом приближении о согласии опытных данных с тем законом распределения, для которого построена вероятностная бумага.Для более объективного построения прямой по опытным точкам рекомендуется использовать метод наименьших квадратов [14]. В рассматриваемом примере удобно построить дискретный ряд распределения, который представлен в таблице 6, а вероятностная бумага с опытными точками и аппроксимирующей прямой на рис. 6. Выбрана бумага для нормального распределения. Как видно из рисунка, экспериментальные точки расположены близко к прямой. Следовательно, исследуемое распределение близко к нормальному. При нанесении на вероятностную бумагу экспериментальных точек частости, соответствующие крайним значениям признака, обычно отбрасываются, так как количество данных для этих значений весьма мало и получается большая погрешность. Таблица 6
|
