Методичка к индивидуальному заданию. Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения
 Скачать 1.66 Mb.
|
|
В графе "Подсчет отдельных значений" приведены три способа подсчета количества значений, попадающих в тот или иной интервал. Эти значки в интервалах ставятся при последовательной обработке табл.1. Каждый значок (точка или линия в любом положении) соответствует одному значению из табл. 1. Если значения, совпадающие с границами интервалов, делятся на два интервала, то, чтобы не ошибиться, рекомендуется эти значения при обработке табл. 1 последовательно записывать во вспомогательную таблицу, одновременно регистрируя их в соответствующем интервале табл. 3. Вспомогательная таблица
Во вспомогательной таблице для примера приведена обработка первых 30 значений табл.1. Когда возникают трудности в построении рядов распределения для выявления закономерностей из-за значительных ошибок измерения (кривые распределения получаются с значительными провалами или гребенчатые), то можно использовать способ построения ряда распределения по среднему квадратическому отклонению [2]. Для этого определяют эмпирическое значение среднего квадратического отклонения  по дискретному или первичному интервальному ряду распределения. Затем от наименьшего значения признака отнимают половину . Это будет новое начало ряда распределения. Все интервалы имеют ширину  . Таким образом, левая граница 1-го интервала равна  , правая граница 1-го интервала равна  , правая граница 2-го интервала будет  и т.д. При может получиться мало интервалов, тогда следует брать ширину интервала  или  . Это требуется при проведении более точных исследований.В случае крайне неравномерно распределенных по размаху варьирования экспериментальных данных, когда в отдельные интервалы попадает весьма малое количество частот (менее 5), удобно использовать метод равночастотных интервалов [13]. Этот метод основан на условии соблюдении равной частоты (равной вероятности) попадания значений признака в любой из  интервалов, т.е.n=const=m и ni/n=  =const.При этом интервалы получаются разной длины. На основании объема выборки принимается решение о количестве интервалов (в тех же пределах, что и ранее, т.е. от 6 до 20) и числе значений признака m в интервале, исходя из условий  ;  .Ширина каждого интервала выбирается по следующему правилу. Для первого интервала 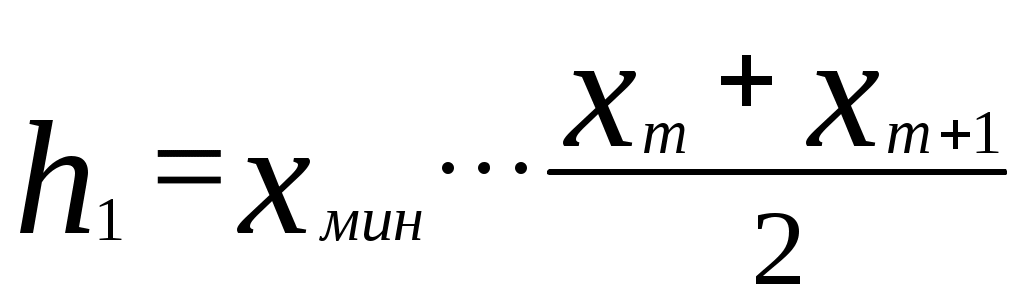 .Для второго интервала 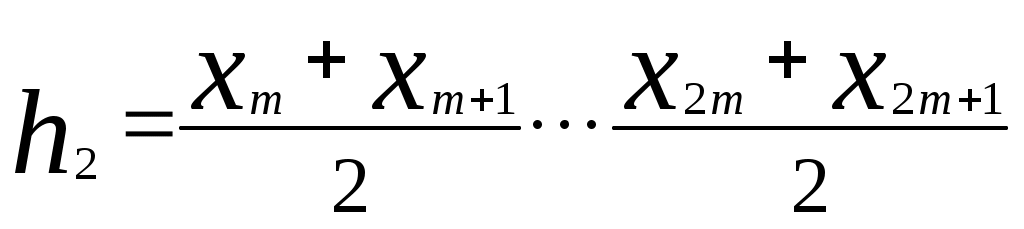 .Для i-го интервала 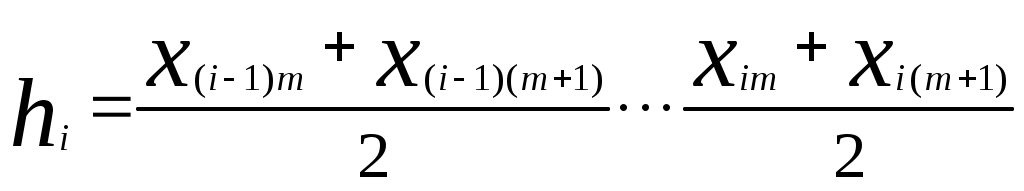 .Для последнего 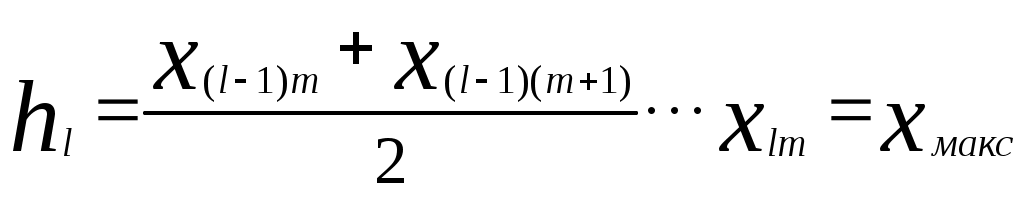-го интервала .В приведенных выражениях обозначение  определяет значение i*m-го признака.Например, выбрано m=12 = const, i = 5, тогда  , т.е. 60-десятое значение признака. Следует заметить, что при этом значения признака должны быть расположены в возрастающем порядке, т.е. должен быть построен вариационный ряд (а иногда и дискретный ряд распределения). Если в вариационном ряде имеется по несколько одинаковых значений признака, то m надо выбирать так, чтобы все эти одинаковые значения попадали в один интервал, а общее количество значений признака в интервале оставалось неизменным, т.е. частота не превышала выбранное ni = m = const. Это удобнее делать по дискретному ряду распределения.В тех случаях, когда  , принимается  так, что  . Разность  включается в один или два интервала с наибольшей плотностью распределения случайной величины (в интервалы, имеющие меньшую длину).Отметим, что при использовании приведенного метода гистограмма должна строиться по плотностям распределения частот  или частостей  .К достоинствам изложенного метода равночастотных интервалов относится то, что он позволяет рациональным образом группировать данные при выборках небольшого объема. 6. ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ КРИВЫХ РАСПРЕДЕЛЕНИЯ Ряды распределения представляют также в виде эмпирических кривых, которые строятся для наглядности и качественной оценки распределения. Используются следующие виды эмпирических кривых: полигон, гистограмма и кумулятивные кривые (ступенчатая и ломаная). Полигон и гистограмма соответствуют изображению дифференциальной функции распределения, а кумулятивные кривые - интегральной. Как правило, для случайных величин дискретного типа употребляются полигон и ступенчатая кумулятивная кривая, а для непрерывных случайных величин - гистограмма и ломаная кумулятивная кривая. Но часто в литературе встречается применение всех четырех типов кривых для непрерывных случайных величин, что, по видимому, нельзя считать вполне обоснованным [2]. Разница между полигоном и гистограммой состоит в следующем. Полигон показывает, что все случайные величины (вариации), попавшие в один и тот же интервал, имеют одинаковое значение признака (это несправедливо для непрерывных случайных величин), равное численно середине интервала, поэтому и кумулятивная кривая имеет разрывы непрерывности. А гистограмма показывает, что все случайные величины, попавшие в один и тот же интервал, равномерно распределяются по интервалу, поэтому кумулятивная кривая имеет рост в интервале. Полигон и гистограмма строятся при равных интервалах по частотам или частостям, а при неравных интервалах - по плотностям распределения частот или частостей. Кумулятивные кривые строятся по накопленным частотам или частостям. Для построения эмпирических кривых необходимо вначале построить интервальный ряд распределения по правилам, указанным в предыдущем разделе. Здесь следует отметить, что кумулятивная кривая гораздо меньше чувствительна к изменениям размера интервала (количества интервалов), чем полигон или гистограмма. Эмпирические кривые (кроме гистограммы) могут быть построены также по дискретному ряду распределения. При построении кривых распределения рекомендуется пользоваться "правилом золотого сечения", по которому высота чертежа должна составлять 5/8 основания. Рассмотрим, как строятся все графики на примере выборки, приведенной в табл.1, хотя это выборка непрерывных случайных величин. Интервальный ряд приведен в табл. 4, а кривые - на рис.1-4. При построении всех эмпирических кривых на оси абсцисс откладываются интервалы шириной  при равных интервалах и  при неравных интервалах. Для построения полигона в серединах интервалов строятся ординаты, пропорциональные частотам или частостям при равных интервалах или пропорциональные плотностям частот или частостей при неравных интервалах. Концы ординат соединяются отрезками прямой (рис.1). Для построения гистограммы (рис.3) нужно на каждом из интервалов как на основании построить прямоугольники. Площадь каждого прямоугольника должна быть пропорциональна частоте или частости в соответствующем интервале. Для этого по оси ординат откладывают плотности распределения частот или частостей. Общая площадь гистограммы для случая, когда по оси ординат откладывают относительную плотность распределения  , должна быть равна единице, поскольку площадь должна совпадать с суммой частостей. Если же на гистограмме изображена абсолютная плотность распределения  , то площади прямоугольников соответствуют частотам интервалов, а площадь всей гистограммы - общему числу случаев (объему выборки). По оси ординат также можно откладывать частоты или частости в случае равных интервалов, при этом изменится только масштаб по оси ординат. Ступенчатая кумулятивная кривая получается путем проведения горизонтальных отрезков прямой между ординатами, построенными в серединах соседних интервалов и пропорциональных накопленным частотам или частостям в соответствующих интервалах. Концы отрезков прямых соединяются вертикальными прямыми (рис.2).Ломаная кумулятивная кривая строится следующим образом. На правых границах интервалов восстанавливаются ординаты, пропорциональные накопленным частотам или частостям. На левой границе первого интервала ордината равна нулю, а на правой границе последнего интервала - единице, если кумулятивная кривая строится по накопленным частостям (рис.4). Таблица 4
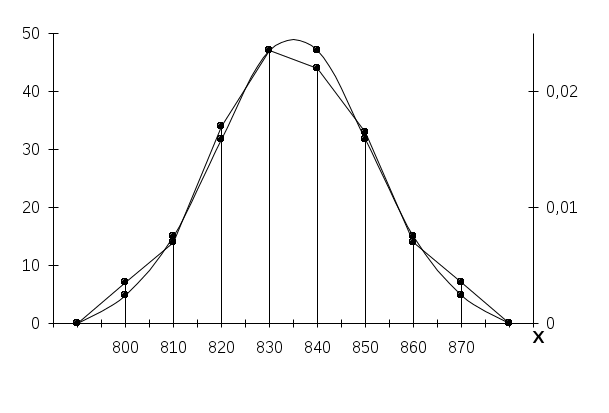    Рисунок 1 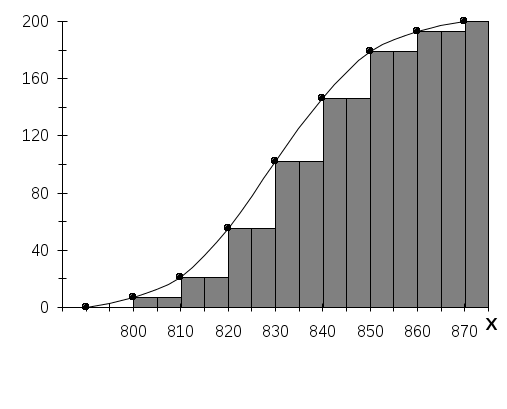   Рисунок 2 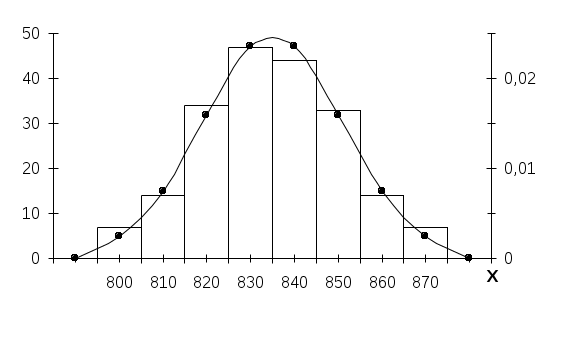  Рисунок 3 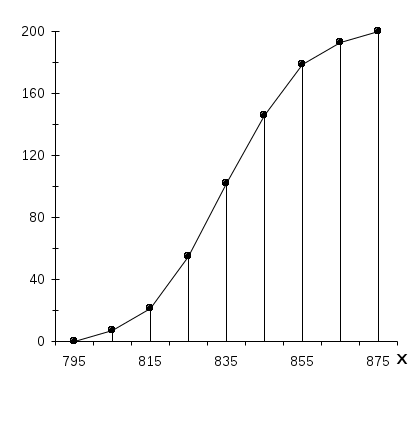 Рисунок 4 7. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ Доверительные границы определяют область, в которой с достаточно большой степенью вероятности находится неизвестная теоретическая функция распределения  . Определим для нее верхнюю  и нижнюю  доверительные границы через известную из опыта эмпирическую функцию распределения  , представленную в ряде распределения накопленными частостями -  .Доверительная вероятность того, что неизвестная теоретическая функция распределения будет лежать в области, ограниченной доверительными границами, определяется выражением:  ,где  - некоторая величина, удовлетворяющая уравнению ,т.е. наибольшее отклонение  теоретической кривой от экспериментальной не превышает значения , установленной для доверительной вероятности  .Таким образом, доверительные границы определяются выражениями: верхняя  ;нижняя  .Всегда численные значения для  и для  .Для определения доверительных границ задаются значением доверительной вероятности  и по таблицам критерия Колмогорова (см. приложение 1) определяют  или  . Связь между ними устанавливается формулой .Значения для  и n = 10..100 можно найти в [15]. Для n>100 в [15] даны значения , по которым определяются . В [1] для  приведены значения при n>100.Для нашего примера при n = 200 зададимся  . Находим в таблицах  .Тогда  .Расчеты  и  сведены в табл.5. Значения  взяты из табл.4.Таблица 5
|
