Методичка к индивидуальному заданию. Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
ПРЕДИСЛОВИЕШирокое внедрение методов математической статистики в теорию и практику конструирования и производства радио- и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения. При этом очень важным является выполнение этапа статистической обработки опытных данных, полученных в результате проведения эксперимента, испытаний изделий и наблюдений за технологическими процессами. Такую обработку можно проводить на ЭВМ и без нее. Но прежде чем использовать ЭВМ, необходимо изучить "механизм" статистической обработки, что можно осуществить только при безмашинной обработке опытных данных. Кроме того, при этом часто удается получить необходимые результаты более оперативно. Естественно, что начальную подготовку по статистической обработке опытных данных будущие инженеры должны получить еще при обучении в институте во время выполнения курсовых и лабораторных работ. Для этой цели предназначается настоящее учебное пособие, которое оказалось необходимым, несмотря на большое количество литературы, посвященной рассматриваемому вопросу. Представляется целесообразным иметь студенту под рукой краткое пособие, в котором порядок обработки был бы четко систематизирован, проанализирован на примерах, приведены различные способы обработки и имелись бы для необходимых случаев ссылки на литературу. В пособии рассматривается статистическая обработка опытных данных, относящихся, как правило, к классу непрерывных случайных величин, которые можно описать одномерной функцией распределения. В пособии не рассматриваются вопросы организации и проведения эксперимента, обработки результатов при малом числе опытов и не приводятся таблицы, необходимые при обработке, а даются ссылки на литературные источники с целью обеспечения возможности читателю расширить свой кругозор. Пособие не претендует на полноту рассмотрения вопросов статистической обработки опытных данных, но во многих практических случаях приведенный объем действий оказывается вполне достаточным. Предполагается, что читатель знаком с основами теории вероятностей и математической статистики. 1. ВВЕДЕНИЕ Прежде чем проводить статистическую обработку опытных данных, необходимо уточнить, какова цель обработки. Это позволит установить минимальный объем действий обработчика. Целями статистической обработки опытных данных могут быть: нахождение закона распределения исследуемой случайной величины, определение числовых характеристик распределения, построение рядов распределения и(или) эмпирических кривых распределений, определение степени связи между исследуемыми случайными величинами и т.д. Достижение поставленных целей зависит от объема выборки. Так, числовые характеристики можно определять для любого количества статистических данных, начиная обычно с десяти. Но для определения закона распределения выборка должна содержать не менее 50 измерений и чем больше, тем лучше. Но в любом случае выборка должна быть случайной, а исследуемая совокупность однородной. Кроме того, должно быть известно, что для наблюдений случайной величины применялись средства измерения с ценой деления, не превышающей 1/5 предполагаемой величины среднего квадратического отклонения исследуемого распределения [1]. При обработке данных эксперимента следует всегда стараться проверить условия применимости (например, нормальности или независимости) статистических процедур. Если это не представляется возможным, то тогда к полученным результатам должно быть осторожное, условное отношение, что, к сожалению, не всегда имеет место. Статистическая обработка опытных данных рассматривается на ряде примеров. В качестве основного примера взят несколько видоизмененный пример, приведенный в [2]. Необходимо, наконец, отметить, что при пользовании указанной в ссылках литературой следует разобраться, что понимается под тем или иным термином (определением) и какая величина обозначена данной буквой или индексом. Так, одно и то же значение вероятности в таблицах одних источников обозначается через Р, а в других это значение соответствует разности 1-Р. Аналогично, при определении доверительных интервалов одно и то же значение критерия В заключение отметим, что приведенный классический метод обработки данных имеет три основных недостатка: - потеря информации при группировке данных; - неоднозначность выбора теоретической функции распределения; - неопределенность при проверке гипотез. 2. ПОРЯДОК СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ОПЫТНЫХ ДАННЫХ При статистической обработке используются графический и аналитический методы отдельно или в совокупности. Графический метод состоит в определении закона распределения и некоторых его параметров с помощью вероятностных (координатных) сеток (вероятностных бумаг). Аналитический метод состоит в вычислении теоретической кривой распределения и ее параметров. Порядок обработки зависит от выбранного метода. Графический метод обработки содержит следующие этапы: построение дискретного ряда распределения; определение закона распределения по вероятностной бумаге (сетке); проверка соответствия эмпирического распределения теоретическому по критериям согласия; определение параметров распределения по вероятностной бумаге (сетке). В необходимых случаях при этом методе обработки могут быть построены интервальный ряд и эмпирические кривые распределения, определены доверительные границы и интервалы. Аналитический метод обработки содержит следующие этапы: построение интервального ряда и эмпирических кривых распределения; определение числовых характеристик (статистик) эмпирического распределения; приближенное определение доверительных границ и интервалов; выбор теоретического распределения; определение оценок параметров теоретического распределения; расчет теоретических кривых распределения (дифференциальной и интегральной) проверка согласия; уточнение доверительных интервалов. В процессе обработки могут выполняться также следующие этапы: исключение грубых ошибок наблюдений; проверка однородности выборок; определение коэффициента корреляции и т.п. Таким образом, в общем случае можно рекомендовать следующий порядок обработки: исключение грубых ошибок наблюдений; построение ряда (рядов) распределения; построение эмпирических кривых распределения; определение доверительных границ; выбор теоретического распределения; проверка правильности выбора теоретического распределения с помощью вероятностных бумаг (сеток) и критериев согласия; определение числовых характеристик (статистик) эмпирического распределения; приближенное определение доверительных интервалов для оценок параметров распределения; определение оценок параметров теоретического распределения; расчет теоретических кривых распределения; проверка правильности выбора теоретического распределения с помощью критериев согласия; уточнение доверительных интервалов; определение коэффициента корреляции. В зависимости от цели обработки и выбранного метода выполняются только необходимые этапы приведенного порядка обработки. Для исключения ошибок и удобства вычислений обработка опытных данных проводится путем обязательного заполнения соответствующих таблиц на всех расчетных этапах. 3. ФОРМЫ ПРЕДСТАВЛЕНИЯ ПЕРВИЧНЫХ ДАННЫХ Первичные данные, полученные в результате проведения наблюдений, опытов, испытаний и т.д., могут быть представлены в виде простого статистического ряда или в виде вариационного ряда. Простой статистический ряд представляет собой совокупность (ряд) значений признака (наблюдаемой случайной величины), расположенных в порядке их получения. Обычно это рабочая таблица, в которую заносятся опытные данные (табл.1).Приведенная таблица содержит выборку, полученную при наблюдениях за какой-то случайной величиной. Таблица 1
Вариационный ряд - это ряд данных, расположенных в порядке возрастания варьирующего признака. При этом одинаковые значения признака не исключаются, а записываются друг за другом. Вариационный ряд может быть представлен в виде таблицы
или построчной записи 800 800 805 805 805 805 805 810 ... ... ........................... ... 870 870 870 870 Приведенный вариационный ряд получен путем обработки данных табл.1. Однако в большинстве случаев первичные данные представляются в виде простого статистического ряда и обычно не имеет смысла строить по ним вариационный ряд. При проведении некоторых видов испытаний регистрируемые первичные данные сразу образуют вариационный ряд. Например, такая запись имеет место в случае испытаний на надежность, когда регистрируются времена исправной работы изделий в партии. Это время записывается в порядке его возрастания, причем одинаковые значения времен работы нескольких изделий повторяются друг за другом. 4. ИСКЛЮЧЕНИЕ ГРУБЫХ ОШИБОК НАБЛЮДЕНИЙ Для исключения грубых ошибок наблюдений, искажающих статистические характеристики распределения, необходимо провести оценку резко выделяющихся членов выборки. Для этого используются различные методы. Конечно, прежде всего следует быть уверенным, что резко выделяющиеся члены выборки не являются результатом ошибки, нарушения условий эксперимента. Если такой уверенности нет, то грубые ошибки сразу следует исключить из дальнейшего анализа. Разработанные методы для оценки резко выделяющихся членов выборки применимы, если известно распределение, которому подчиняются наблюдаемые случайные величины. Их применение при других распределениях может привести к серьезным ошибкам [3]. Это часто не указывается в литературе, где приводятся такие методы. Большинство методов разработано для случаев, когда исследуемые величины подчиняются нормальному распределению. Эти методы (часто они носят название критериев), как правило, требуют предварительного вычисления среднего значения и среднего квадратического отклонения исследуемой величины. Во всех методах рассчитываемая величина сравнивается с критическим значением этой величины, найденным из соответствующих таблиц при выбранном проценте риска. После чего принимается решение о том, является ли резко выделяющееся значение случайной величины грубой ошибкой и его следует отбросить или оно не подлежит исключению из выборки. Рассмотрим методы (критерии), которые применяются при нормальном распределении исследуемой случайной величины. В литературе приводятся следующие методы (критерии): критерий, основанный на теореме Р.Фишера[4], критерий типа r [4], упрощенные критерии [4], метод Грэббса [5], метод Романовского [5], метод исключения при известной [6], оценка анормальности результатов измерений при известной генеральной дисперсии [3], метод исключения при неизвестной [6], оценка анормальности результатов измерений при неизвестной генеральной дисперсии [3]. Следует отметить, что в [5] и [6] не указано, что перечисленные методы применимы только при нормальном распределении. Критерий, основанный на теореме Фишера [4], приведен в одной из работ В.Н.Романовского. В нем рассматривается неравенство 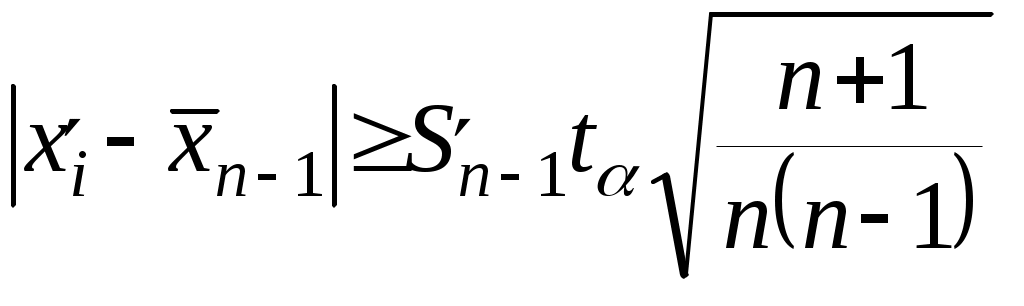 , ,где n - число членов выборки; 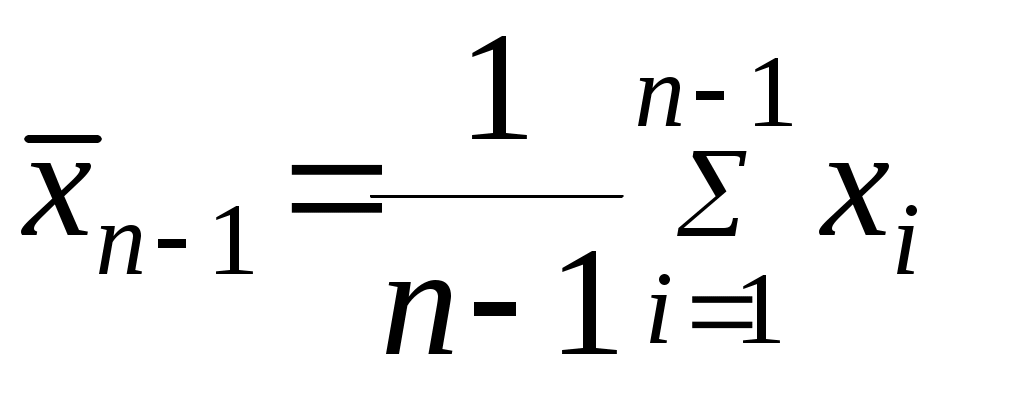 - среднее значение исследуемой величины, подсчитанное при исключенном резко выделяющемся члене выборки - среднее значение исследуемой величины, подсчитанное при исключенном резко выделяющемся члене выборки |
