Методичка к индивидуальному заданию. Широкое внедрение методов математической статистики в теорию и практику конструирования и производства радио и электронной аппаратуры требует от конструкторов и технологов освоения этих методов и умения их применения
 Скачать 1.66 Mb.
|
Таблица 7
После определения всех условных моментов можно найти числовые характеристики распределения  ; ; .Так как результат для А положительный, то, следовательно, асимметрия правосторонняя (математическое ожидание расположено правее моды).(надо 2,600 в квадрате = 2,6002) у меня формулы не работают  .Эксцесс отрицательный, следовательно вершина эмпирической кривой распределения лежит ниже вершины теоретической кривой нормального распределения. Поскольку асимметрия и эксцесс малы по абсолютной величине, следовательно, исследуемое распределение близко к нормальному. Для определения моды можно использовать следующую формулу [2]:  .Если метод "условного нуля" будет применяться к дискретному ряду, то при проведении эксперимента необходимо обеспечить равный шаг между дискретными значениями признака, чтобы условные варианты были целыми числами. В тех случаях, когда достаточно ограничиться определением среднего и имеется интервальный ряд, можно использовать следующее выражение [5]: 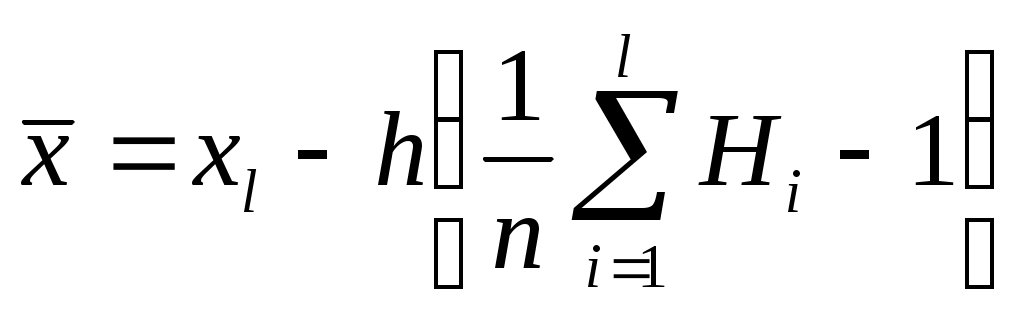 ,где  - середина последнего интервала; - сумма накопленных частот всех интервалов.Для нашего примера (табл.4):   .9.3. Применение статистик для выбора закона распределения Коэффициент вариации, коэффициенты асимметрии и эксцесса могут использоваться для приближенного выбора или приближенной оценки правильности выбора теоретического распределения [10]. Так, для коэффициента вариации известны диапазоны значений, в которых он находится, для того или иного закона распределения.
Как следует из таблицы, возможна неоднозначность выбора. Для того, чтобы применить коэффициенты асимметрии и эксцесса к выбору или оценке выбора теоретического закона, необходимо рассчитать их средние квадратические отклонения по формулам  и  .Если найденные значения коэффициентов асимметрии и эксцесса отличаются от их значений для теоретического распределения не более чем на утроенные средние квадратические отклонения, то теоретическое и эмпирическое распределения согласуются. Причем, должны выполняться одновременно оба условия  и  ,где  и  - соответствующие значения коэффициентов асимметрии и эксцесса для теоретического распределения, взятые из таблиц, например [3].Для нормального закона  , следовательно, используются условия и  .Недостаток метода заключается в приближенности оценки, так как правило «трёх сигм» является эмпирическим. Для нашего примера А=0,025 и Е=-0,380;  ; .Следовательно, в нашем случае согласие можно считать хорошим. При объёме выборки n60 с точностью не хуже 10% можно пользоваться выражениями  и  .В [9] приведены формулы для основных ошибок статистик, если исследуемое распределение подчиняется нормальному закону:   ; .При этом указывается, что основная ошибка статистики определяет те границы, в которых с вероятностью 0,683 заключено неизвестное значение соответствующего параметра, т.е. в пределах S. Если найденные значения А и Е лежат в пределах своих двукратных основных ошибок, т.е.  и  , то исследуемое распределение можно считать нормальным [9].Для рассматриваемого примера основные ошибки статистик равны  , т. е.   , т. е.   , т.е.   , т. е.   , т. е.  В нашем примере 0,025<2•0,173 и 0,380<2•0,346, т.е. распределение нормальное. Если приведённые формулы для основных ошибок статистик используются при анализе распределений, отличных от нормального, то границы, в которых с вероятностью 0,683 заключается неизвестное значение соответствующего параметра, будут определены только приближённо. 9.4. Вычисление доверительных интервалов для числовых характеристик Поскольку точечные оценки параметров распределения являются случайными, то обычно для них определяют доверительные интервалы, в которых с доверительной вероятностью находятся истинные значения параметров распределения - интервальные оценки. Точное определение интервалов возможно только, если известен закон распределения случайной величины. Пока такой закон неизвестен, доверительные интервалы определяют приближённо, полагая справедливым нормальный закон распределения случайной величины. Уточнение проводится после выбора закона распределения и проверки его согласия с эмпирическим распределением. Доверительный интервал для математического ожидания имеет границы  и  ,где  .Для определения следует найти по таблицам (см. приложение 2) значения  при выбранной доверительной вероятности и числе степеней свободы k=n-1. Обычно рекомендуется брать 0,90.Таблицы для называются по-разному, в том числе: распределение Стьюдента, значения коэффициента Стьюдента и т.п. В некоторых источниках [10,19] значения приведены для одностороннего критерия при доверительной вероятности 1- . Поэтому при вычислении двухсторонних границ значения t следует брать при  .Для примера выбираем  =835, S=16, n=200 и =0,95. При k=n-1200 по[15, табл.11.5] или[18, табл.4] находим =1,972. В [9,табл. XVII] значение =1,972 находим уже при уровне значимости1-=1-0,95=0,05. По [10,19, табл. приложения 3] и [9, табл. XVII] значение  определяем при доверительной вероятности .Тогда  .Следовательно,  и  .Доверительный интервал для теоретического среднего квадратического отклонения имеет границы  и  ,где  .Значения q определяются через доверительные вероятности  , таблицы для которых приведены в [2,18]. Доверительная вероятность определяет вероятность нахождения генеральной характеристики в доверительном интервале .В этом случае является двусторонней доверительной вероятностью. Могут быть односторонние доверительные вероятности  и  .В этом случае  и  обычно имеют большие значения, например 0,95. Связь между двусторонней и односторонними доверительными вероятностями устанавливается выражением .При  имеем  или  . Для расчётов доверительного интервала при заданной можно использовать также выражения и  и [6, табл. V] для нахождения q. Однако удобнее для определения доверительных границ использовать формулы вида  и  .Расчёт по этим формулам можно проводить по таблицам, приведённым в [3,6,10,15,19]. Отметим особенности расчёта по указанной литературе. В [6,10,19] доверительные границы определяются для двусторонней доверительной вероятности . В [6] коэффициенты  и  обозначены соответственно через z1 и z2, а - через p. В [19] необходимо рассчитать и по формулам и  ,где  - процентные точки хи - квадрат распределения, определяемые по таблицам [19], а  Для использования таблиц, приведённых в [3], следует или задаться двусторонней доверительной вероятностью  и по ней выбрать односторонние доверительные вероятности  и  из условия  , или задаться непосредственно и . В данном случае  , и она должна быть близка к нулю. Затем по таблицам определяются для значение  , а для значение  . Тогда и  .В [15] коэффициенты и обозначены соответственно через  и  и определяются они для односторонних доверительных границ, причём . Следовательно, если задана двусторонняя доверительная вероятность , то следует найти и по этому значению определить и .Для примера зададим n=19 и.=0,99 и покажем определение и по различным источникам. По [6, табл. VI] и [10, приложение 6] имеем при k=n-1=18, что  и  . По [19, приложение 2] находим для значение  ,и для  значение  при k=n-1=18.Тогда  и  .Для использования [3, табл. П6] задаёмся  и  , так что  . Находим по таблице, что  и  при k=n-1=18. Тогда и  .Для использования (см. приложение 3) задаёмся  близким к единице, но так как задано =0,99, то определяем .По таблице находим для k=n-1=18 значения  и  . Т.е. при односторонних доверительных вероятностях  двусторонняя доверительная вероятность =0,99. Соответственно при  имеем =0,98 и т.д.Следует заметить, что в [6] формулы вида  используются только при малом объёме выборки, а при большом объёме используются формулы вида  . Но в других источниках [3,10,15,18,19] таких ограничений нет. Например, в [10,15] вычисления по формулам вида проводятся при k, достигающем значений 100...200 и даже 1000 [3].10. РАСЧЁТ ТЕОРЕТИЧЕСКИХ КРИВЫХ РАСПРЕДЕЛЕНИЙ И ОЦЕНКИ ИХ ПАРАМЕТРОВ Расчёт теоретических кривых распределений может проводиться как для дискретного ряда, так и для интервального ряда. В интервальных рядах расчёт проводится по серединам интервалов или по интервалам. Расчёт по интервалам для интервальных рядов является более удобным и правильным. Расчёт дифференциальной кривой теоретического распределения для середин интервалов проводится по плотности распределения  , определяемой по значениям признака  в серединах интервалов. Теоретическая частость находится по формуле .Расчёт дифференциальной кривой по интервалам проводится по следующему выражению:  ,где F(x) - интегральная функция распределения; x1и x2 - значения левых и правых границ интервалов. Теоретические частоты в обоих случаях вычисляются через теоретические частости  .Параметры законов распределения находятся по опытным данным в виде точечных или интервальных оценок. Методы нахождения параметров закона распределения делятся на графические и аналитические - метод моментов и метод наибольшего (или максимального) правдоподобия. От точечных оценок, как указано выше, требуется, чтобы они были состоятельными, несмещёнными и эффективными. Названные методы не всегда обеспечивают эти требования и тем более одновременно, т.е. чтобы оценка отвечала сразу всем требованиям. Оценки, полученные графическим методом, являются наименее точными. Более точно определяются оценки методом моментов. Этот метод состоит в том, что теоретические моменты приравниваются эмпирическим. Образуется система, в которой количество уравнений равно количеству неизвестных параметров теоретического распределения. Решая систему, находят неизвестные параметры. Метод моментов позволяет доказать, что для случайной величины x, распределённой по любому закону, оценками математического ожидания а и дисперсии  являются и  , найденные для исследуемой выборки.Метод моментов весьма простой и часто используется, хотя оценки параметров при этом получаются, как правило, смещёнными и малоэффективными. Наиболее точные оценки получаются по методу максимального правдоподобия, но они могут оказаться смещёнными. Этот метод, как и метод моментов, может применяться только при известном законе распределения случайной величины. Суть метода заключается в составлении функции правдоподобия, которая для непрерывных случайных величин имеет вид  ,где n - число измеренных значений x (объём выборки); - неизвестный параметр теоретического распределения; k - число неизвестных параметров распределения. По методу максимального правдоподобия за оценку выбирается такое значение , которое обеспечивает максимум L, что будет при  .Удобнее находить, однако, не экстремум функции L, а экстремум функции lnL, т.е.  .Число таких уравнений берётся равным числу неизвестных параметров  . Из образовавшейся системы находят оценки неизвестных параметров  . Этот метод иногда приводит к сложным уравнениям. Но он обладает рядом преимуществ по сравнению с методом моментов [10]. Оценки получаются состоятельные и эффективные. Смещение можно устранить введением поправок, и, кроме того, с ростом n смещение уменьшается, т.е. оценки становятся несмещёнными. Возможно приближённое решение уравнения, а также системы уравнений максимального правдоподобия [19].В связи с вышеизложенным, можно рекомендовать следующий порядок получения точечных оценок параметров распределения. Вначале их получают графическим методом по вероятностной бумаге. Затем они могут быть уточнены или, если графический метод не использовался, впервые вычислены методом моментов или методом максимального правдоподобия [19]. После выбора закона распределения производится также уточнение и интервальных оценок. Различные законы распределения (их форму, расчётные формулы для плотности и функции распределения, а также для моментов  , A и E) можно найти в [3,9,15,16,20..24,32 и др.]. 10.1 Нормальное распределение Формулы для плотности и функции нормального распределения имеют вид 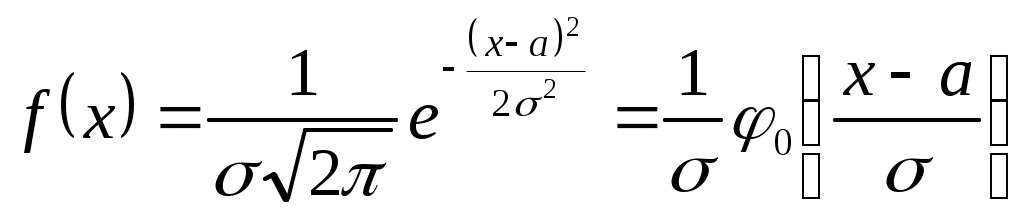 ; 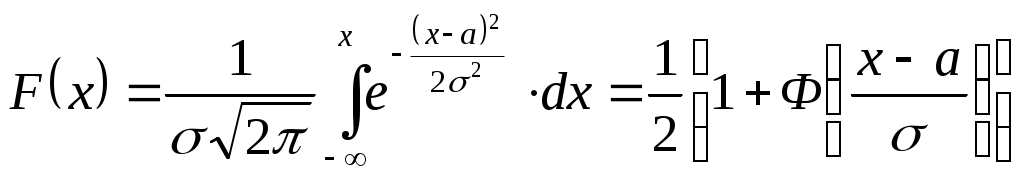при - < x < и > 0. Нормальное распределение является двухпараметрическим. Его параметрами являются математическое ожидание  и среднее квадратическое отклонение  . Прежде, чем проводить расчёт теоретической кривой, необходимо найти значения и . Для нормального распределения  ,  .10.1.1. Оценка параметров графическим методом После нанесения прямой линии по экспериментальным точкам на вероятностной бумаге определяют оценки параметров распределения по углу наклона прямой и отрезкам, которые она отсекает на осях координат. Для нашего примера нормальная вероятностная бумага с нанесёнными экспериментальными точками и аппроксимирующей прямой линией приведена на рис. 6. Поскольку распределение нормальное, то F(x)=0,5 соответствует математическому ожиданию . На уровне F=0,5 проводим прямую, параллельную оси абсцисс. Точка А пересечения прямых соответствует точечной оценке математического ожидания  .Точечная оценка среднего квадратического отклонения  находится по углу , образованному прямыми. Для определения используется следующая формула, справедливая при длине шкалы по оси ординат, равной 300 мм, что соответствует изменению F от 0,001 до 0,999 [15] ,где  - масштабный коэффициент для оси абсцисс;K - ширина графика по оси абсцисс в мм (длина отрезка в мм по оси абсцисс, соответствующего R); R - размах варьирования. По графику находим, что K=140 мм, AB=60 мм, BC=90 мм. Известно, что R=70. Тогда   .С целью уменьшения размеров рис.6 на ось ординат нанесена только часть шкалы от 0,01 до 0,96, что вполне достаточно для построения графика и соответствует 204 мм. 10.1.2. Оценка параметров по методу моментов Для нормального распределения начальный момент 1-го порядка 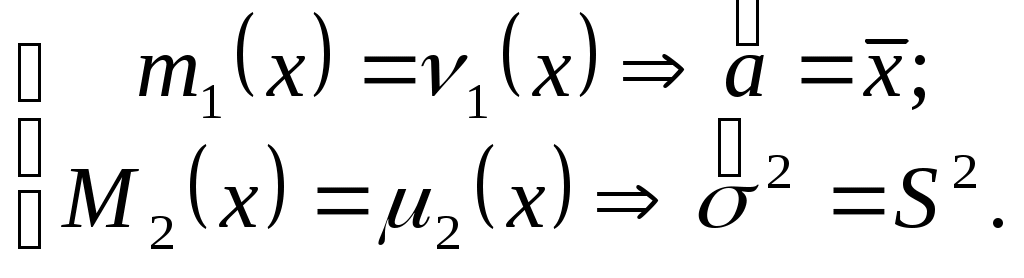 , центральный момент второго порядка  . Соответствующие моменты эмпирического распределения  и  . Приравнивая моменты, находим При этом является состоятельной, несмещённой и эффективной оценкой . будет состоятельной, несмещённой и эффективной оценкой только в случае, если известно , в противном случае она не обладает свойствами эффективности. Чтобы было несмещённой оценкой , её следует вычислять по формулам при n>30; при n30для интервального ряда. 10.1.3. Оценка параметров по методу максимального правдоподобия Функция правдоподобия для нормального распределения случайной величины x имеет вид 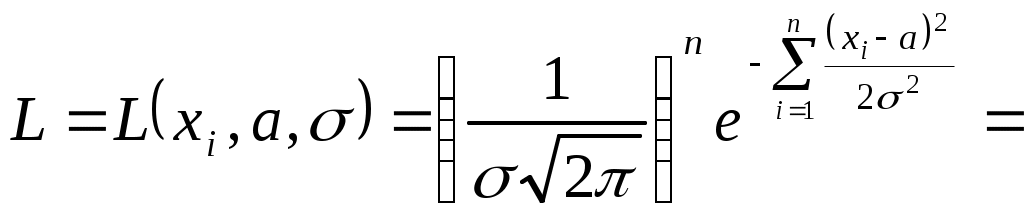 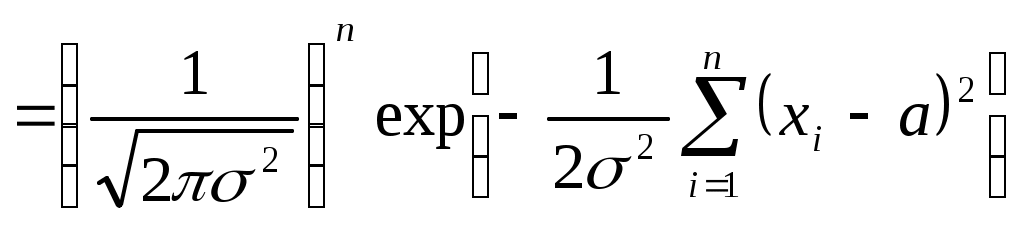 .Логарифмическая функция правдоподобия равна  .Дифференцируем lnL последовательно по a и по и получаем систему уравнений для их оценок ; .Отсюда находим  ; Оценка будет смещённой при n30. 10.1.4. Определение доверительных интервалов Доверительные интервалы (интервальные оценки) для параметров и нормального распределения при заданной доверительной вероятности определяются по методике, приведённой в п. 9.4.10.1.5. Расчёт теоретической кривой нормального распределения Расчёт проведён для середин интервалов и по интервалам. При вычислении кривой распределения для середин интервалов воспользуемся нормированной и центрированной плотностью вероятности нормального распределения  ,где  - нормированное отклонение.Функция  являе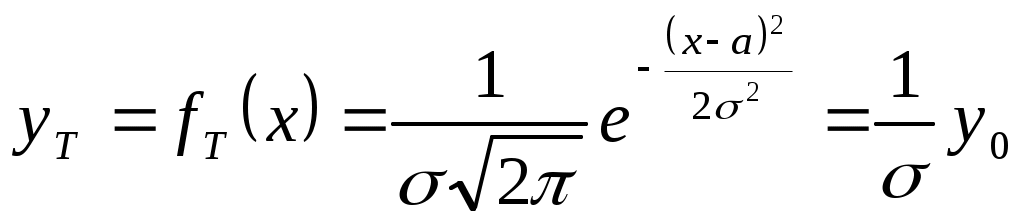тся табулированной и определяется через t (см. приложение 4). При этом  .Тогда  Средняя плотность эмпирического распределения  Теоретические частости для середин интервалов будут равны  а теоретические частоты для середин интервалов определятся выражением  .Вычисления проводятся с помощью табл. 8. После вычисления теоретических частот их необходимо выровнять на основании следующих положений: - частоты могут выражаться только целыми числами; - сумма теоретических частот должна быть равна сумме эмпирических частот с принятой точностью; - в случае нормального распределения принимается во внимание знак эксцесса и частоты должны быть поровну распределены относительно .В рассматриваемом случае знак у эксцесса отрицательный, т. е. вершина теоретической кривой распределения должна лежать выше вершины эмпирической кривой. Поэтому частоты интервалов, близких вершине, округляем в большую сторону. В табл. 9 приведён расчёт теоретических интегральных кривых распределения на основе данных табл. 8. Кривые, рассчитанные в табл. 8 и 9, представлены на рис. 1 и 2. Операцию расчёта теоретических частостей и частот иногда называют вычислением выравнивающих частостей и частот [9]. При вычислении нормальной кривой распределения по интервалам (что более удобно и правильно) используется табулированный интеграл вероятностей (функция Лапласа)  , где - нормированное отклонение.Таблица 8
|
(3x4)
(4x5)
(4x6)
(4x7)
(3x94)
