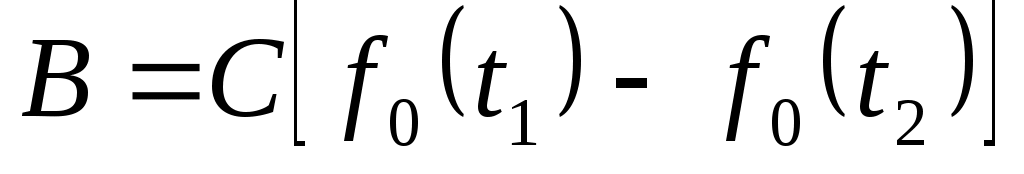 ; ;
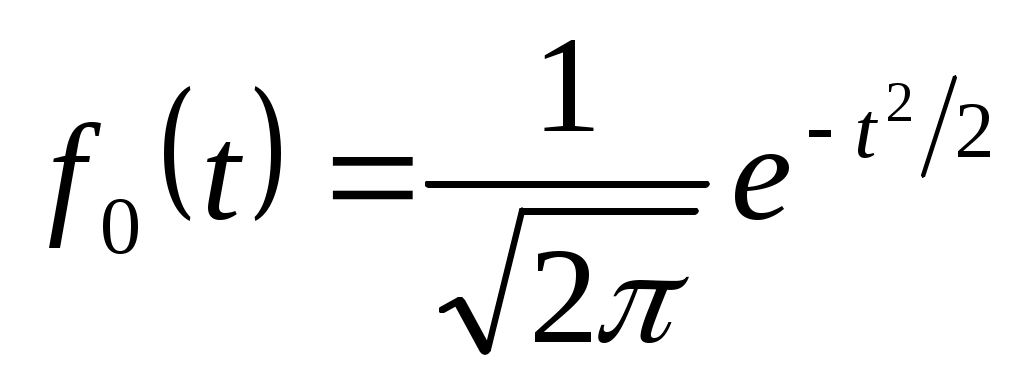 - нормированная плотность распределения. - нормированная плотность распределения.
Приравниваем теоретические и эмпирические моменты и находим 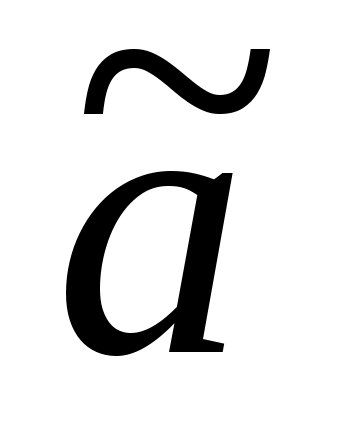 и из системы уравнений (см. также [25, с.274]): и из системы уравнений (см. также [25, с.274]):
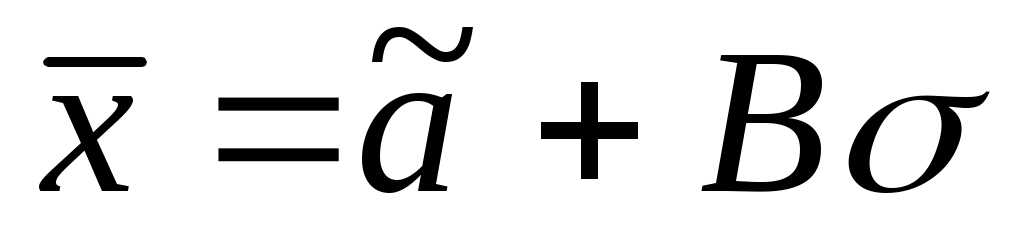 , ,
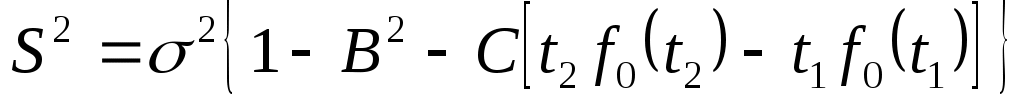 . .
В уравнениях известны 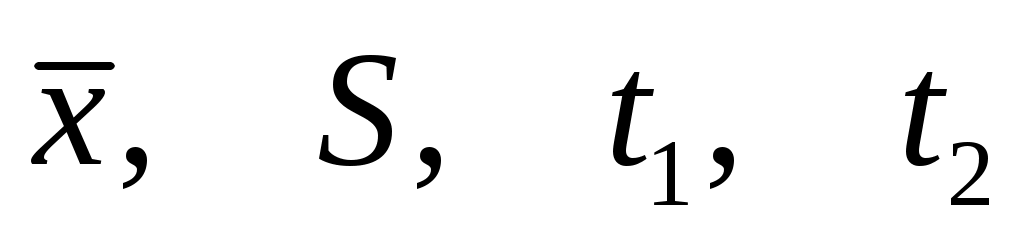 . .
При симметричном двустороннем усечении 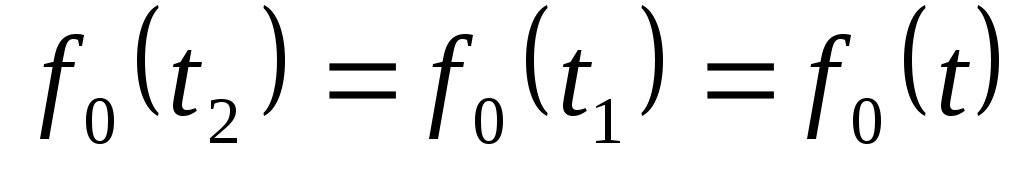 . .
Следовательно, В=0. Тогда 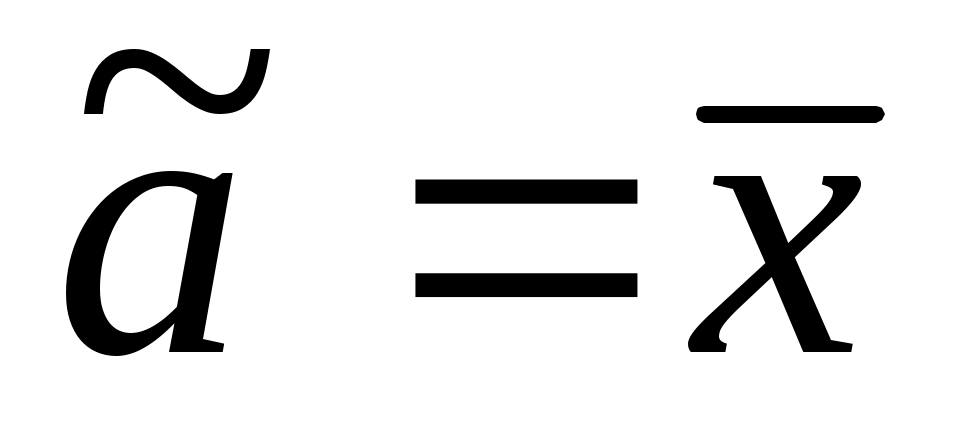 и и
 . .
Определить 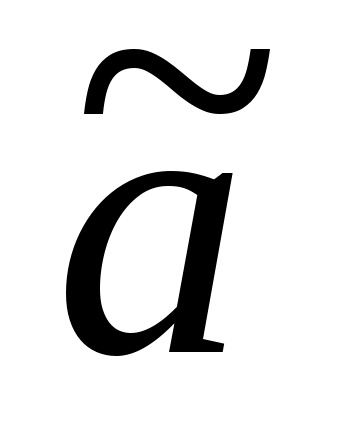 можно также, если найти моду эмпирического распределения. При этом можно также, если найти моду эмпирического распределения. При этом 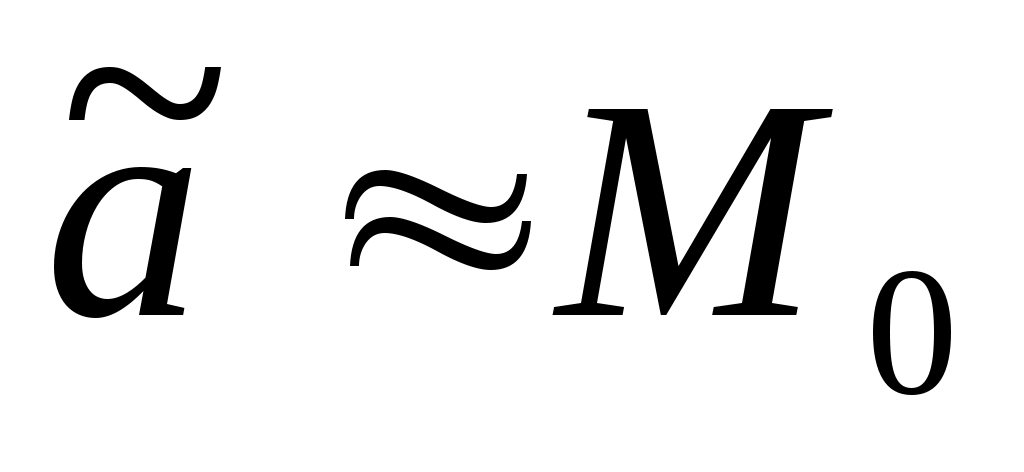 . При одностороннем усечении нормального распределения ориентировочное значение можно найти следующим образом. . При одностороннем усечении нормального распределения ориентировочное значение можно найти следующим образом.
Если 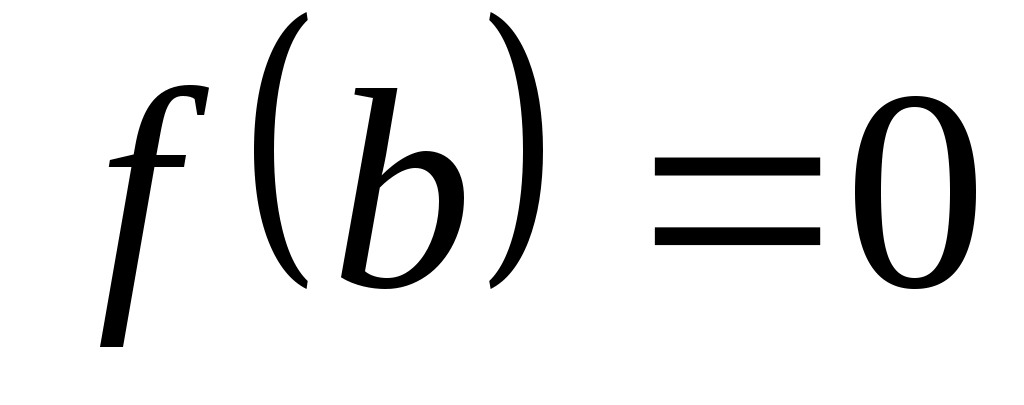 , где , где 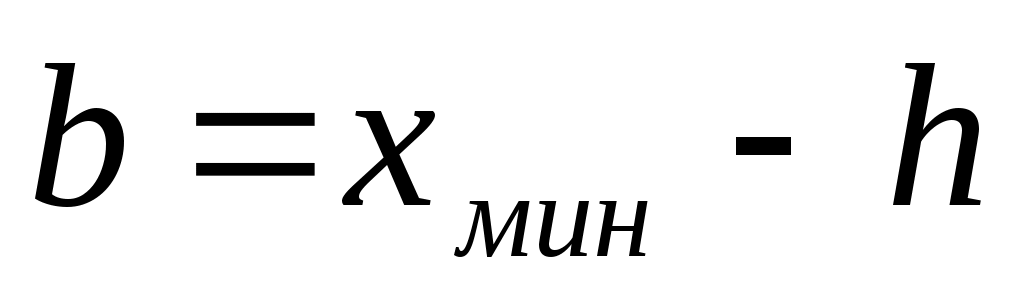 , то , то
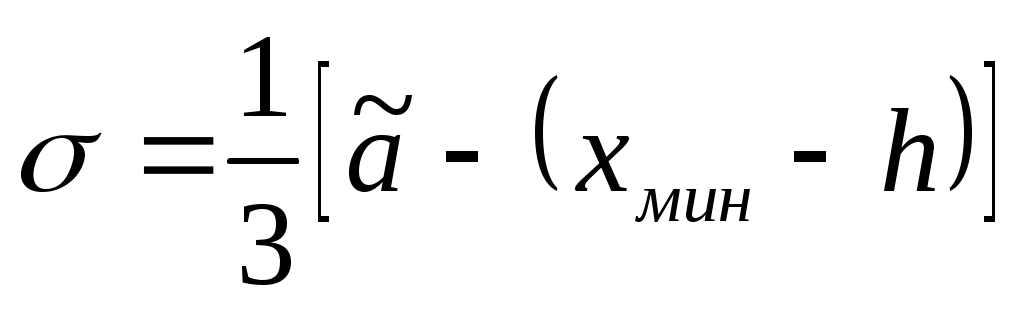 . .
Если 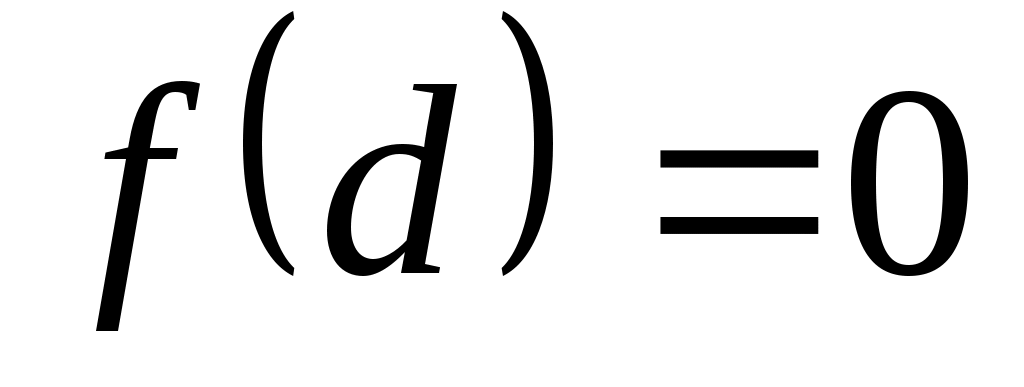 , где , где 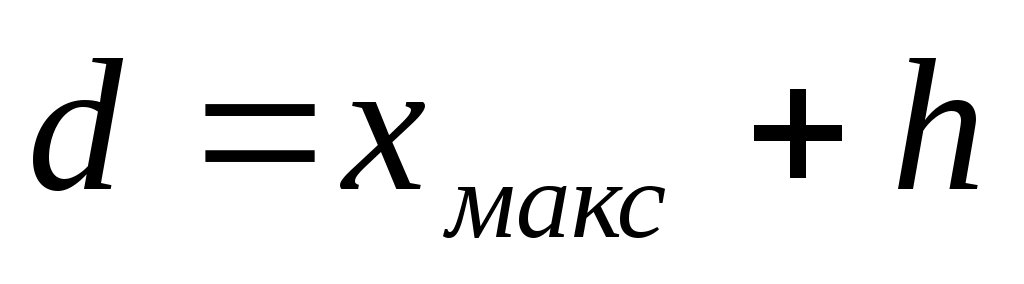 , то , то
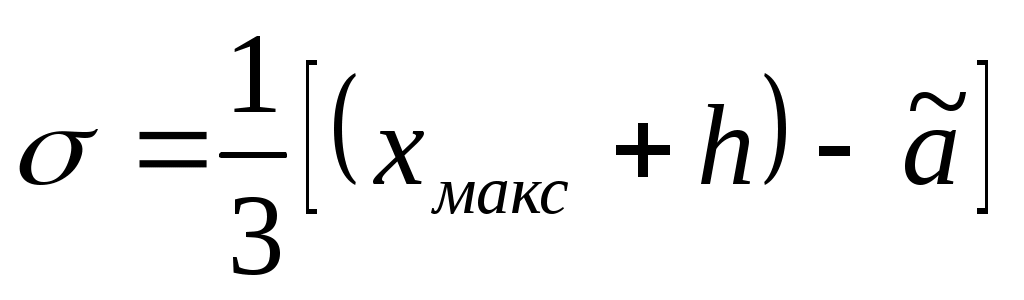 . .
Следует отметить, что если для симметричного двустороннего усеченного нормального распределения 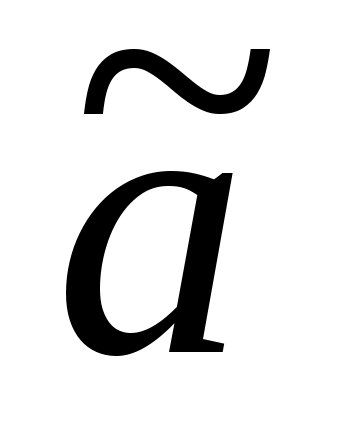 -b2 и d– -b2 и d–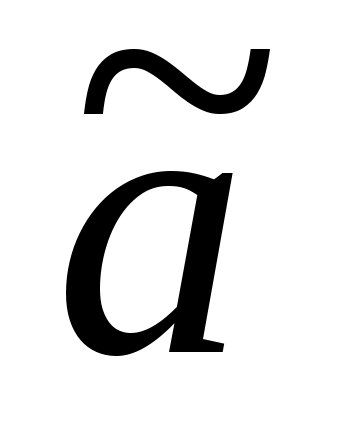 2, то можно полагать с ошибкой не более 10%, что параметры такого распределения равны параметрам нормального распределения и С1, т.е. m1(x)a и M2(x)2 и усеченное нормальное распределение достаточно точно аппроксимируется обычным нормальным распределением. Дополнительные сведения об усеченном нормальном распределении можно найти в [3,с.143 и 395; 15,с. 119; 21,с.429]. 2, то можно полагать с ошибкой не более 10%, что параметры такого распределения равны параметрам нормального распределения и С1, т.е. m1(x)a и M2(x)2 и усеченное нормальное распределение достаточно точно аппроксимируется обычным нормальным распределением. Дополнительные сведения об усеченном нормальном распределении можно найти в [3,с.143 и 395; 15,с. 119; 21,с.429].
Теоретическая частость (вероятность) будет равна
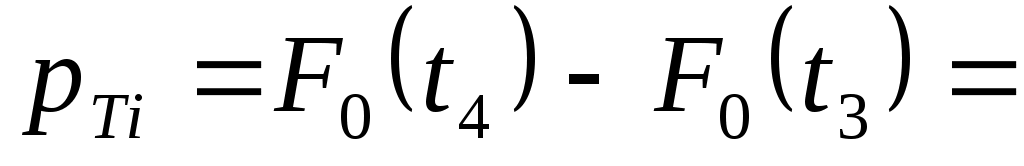
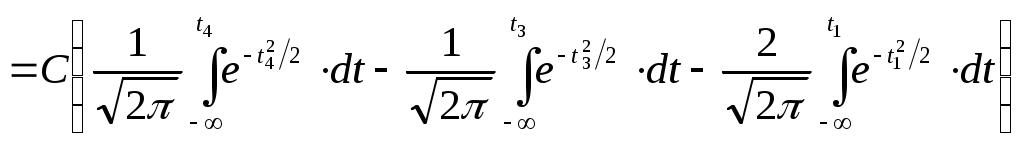 , ,
где 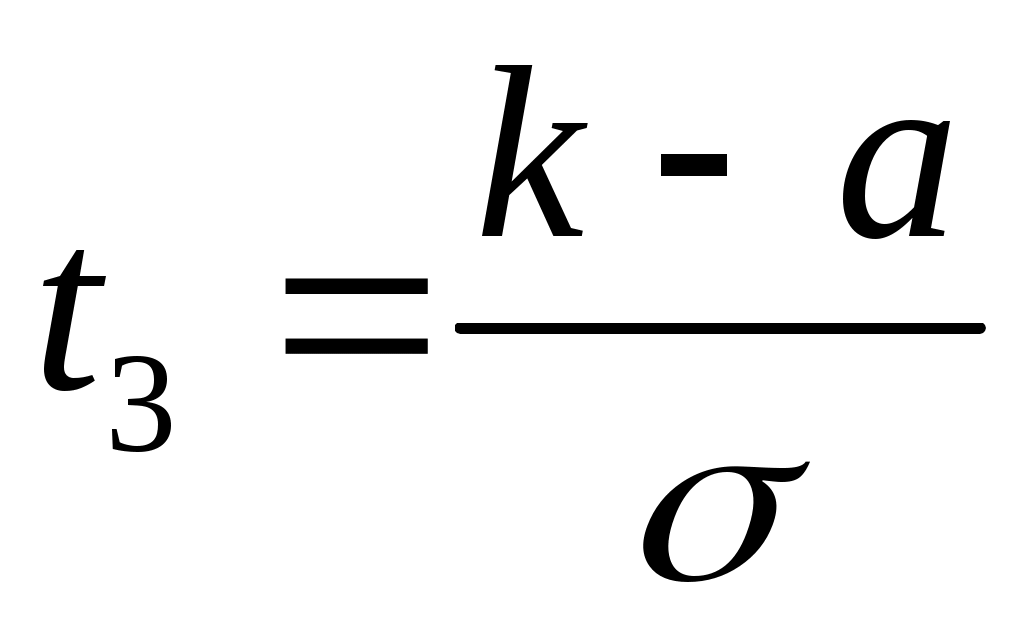 , , 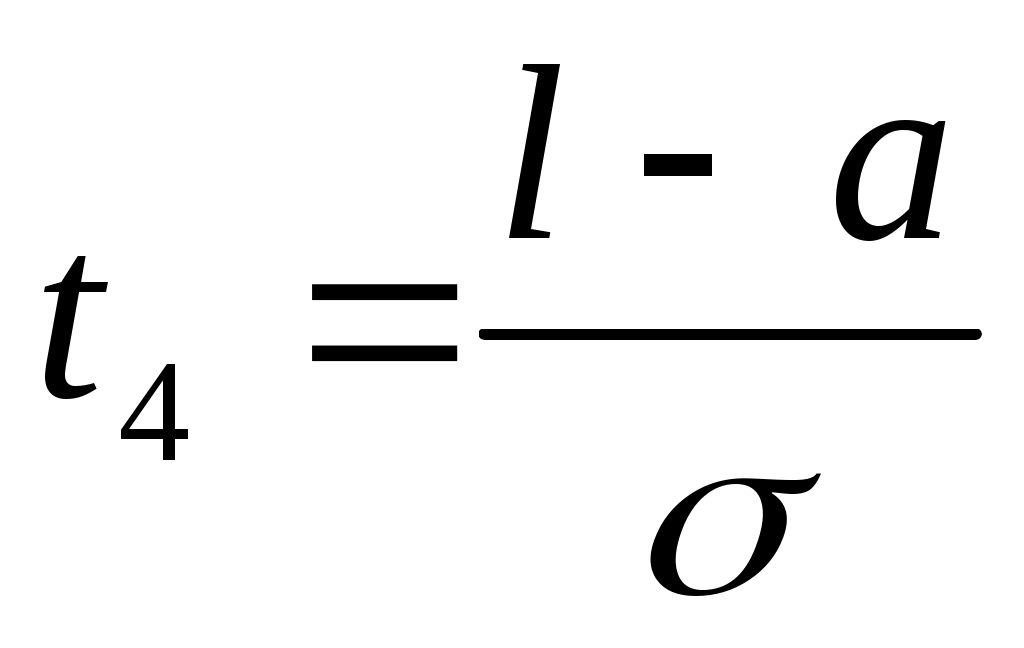 , ,
k – левая граница интервала,
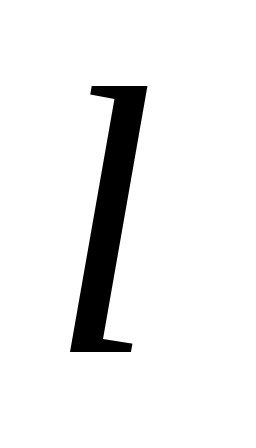 – правая граница интервала. – правая граница интервала.
10.2.2. Логарифмически нормальное распределение
Случайная величина имеет логарифмически нормальное распределение, если логарифм этой величины распределен нормально.
Плотность и функция распределения определяются по формулам
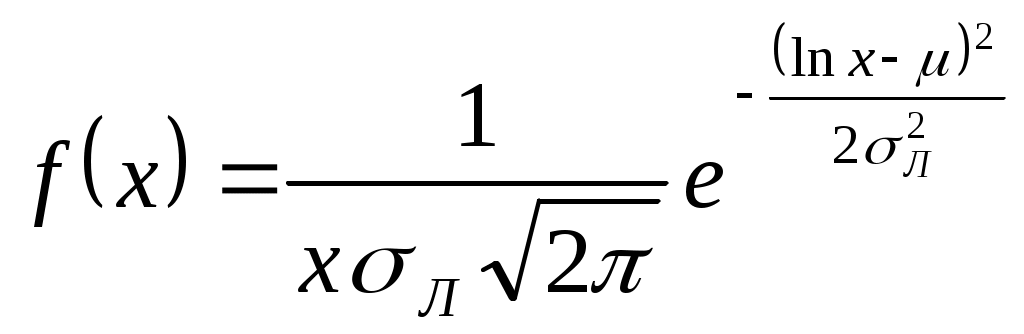 ; ;
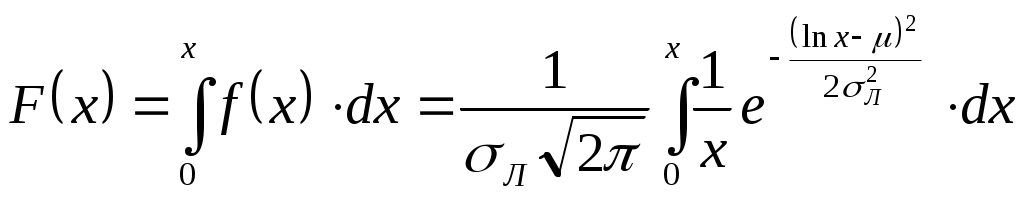 . .
Обозначив 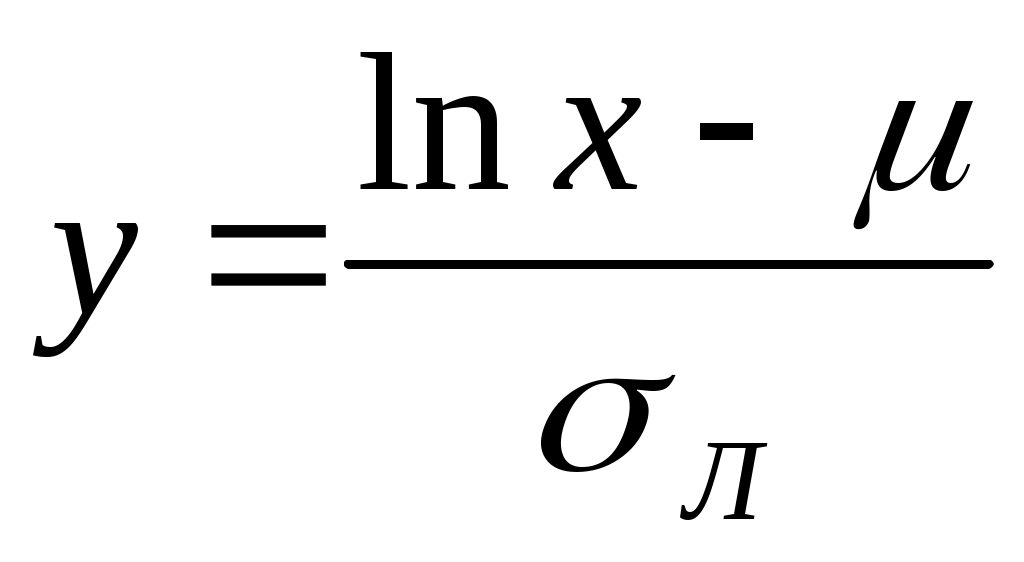 , имеем , имеем 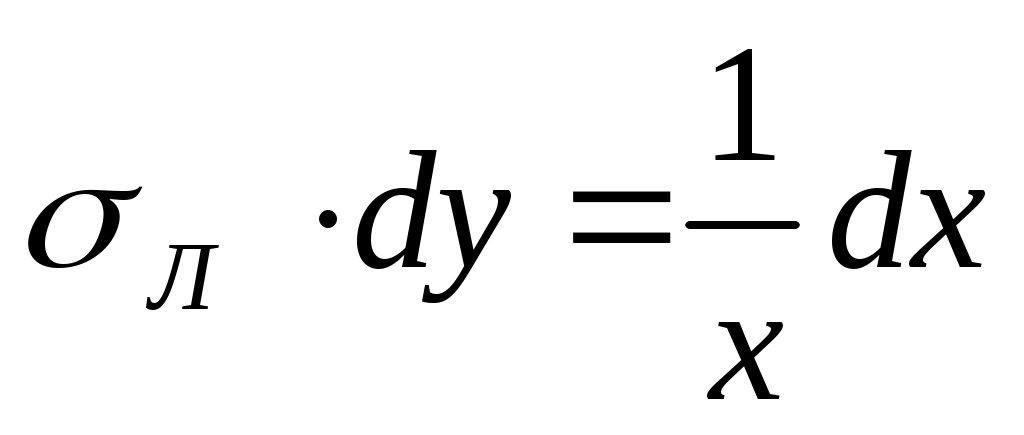 ; ; 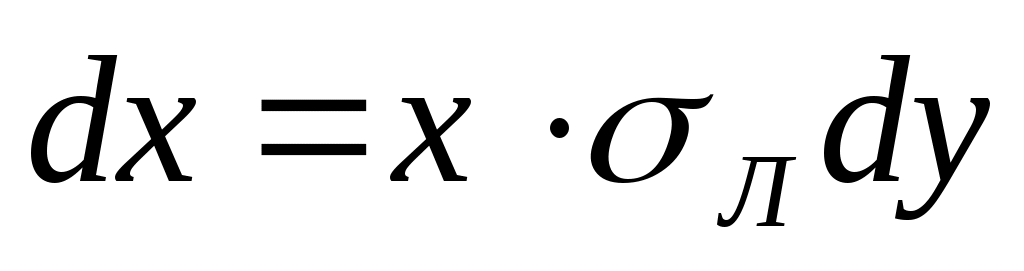 и и 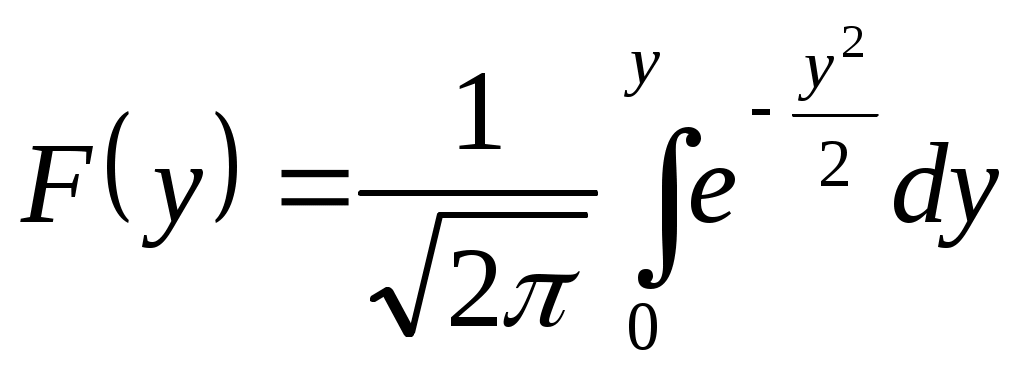 находим по y в [15, табл. 1.2]. находим по y в [15, табл. 1.2].
Оценки параметров распределения и 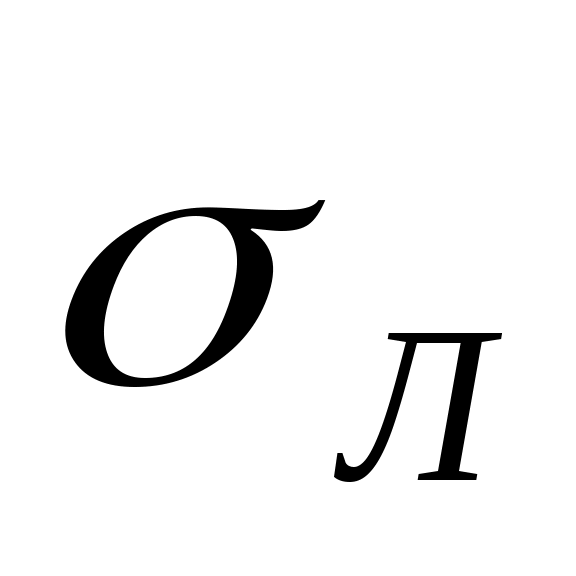 определяются для дискретного ряда по формулам определяются для дискретного ряда по формулам
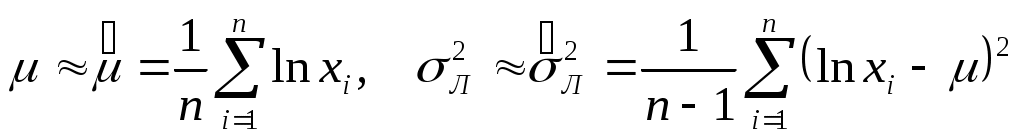 , ,
и для интервального ряда по формулам
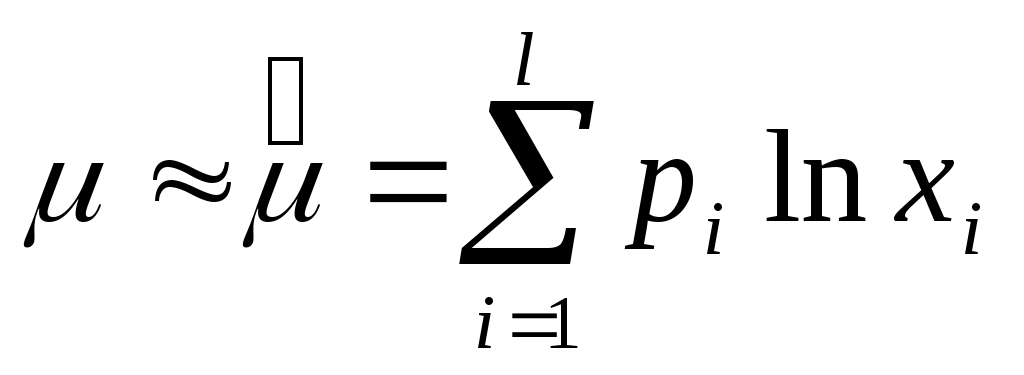 , , 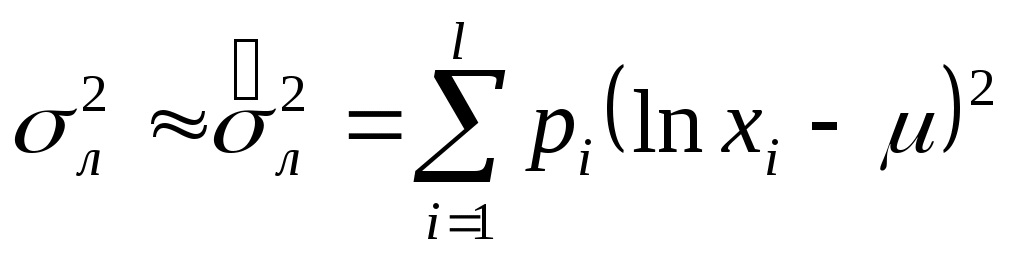 , ,
где 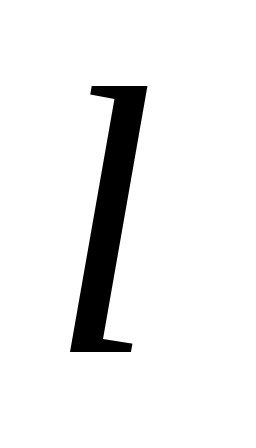 - количество интервалов. - количество интервалов.
Плотность распределения можно записать в следующем виде
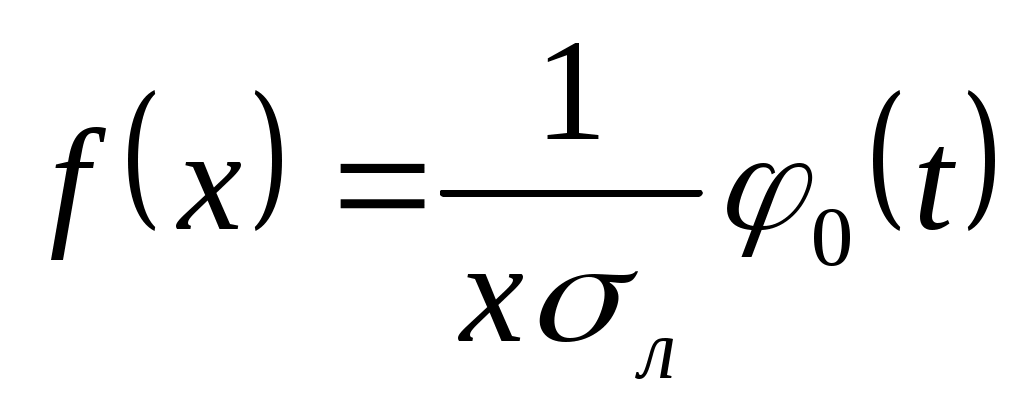 , ,
где 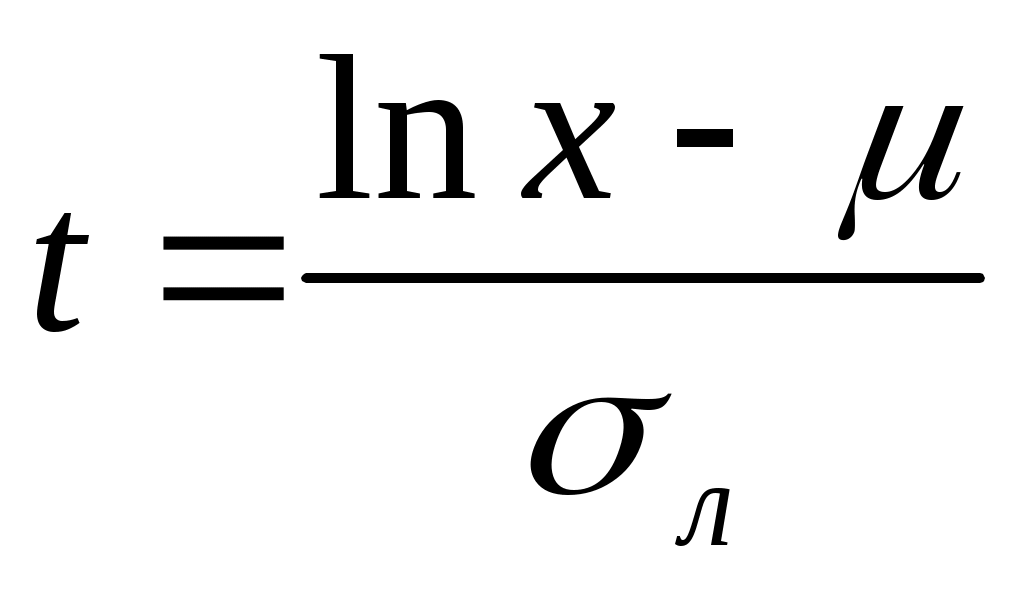 - нормированное отклонение. - нормированное отклонение.
Значения 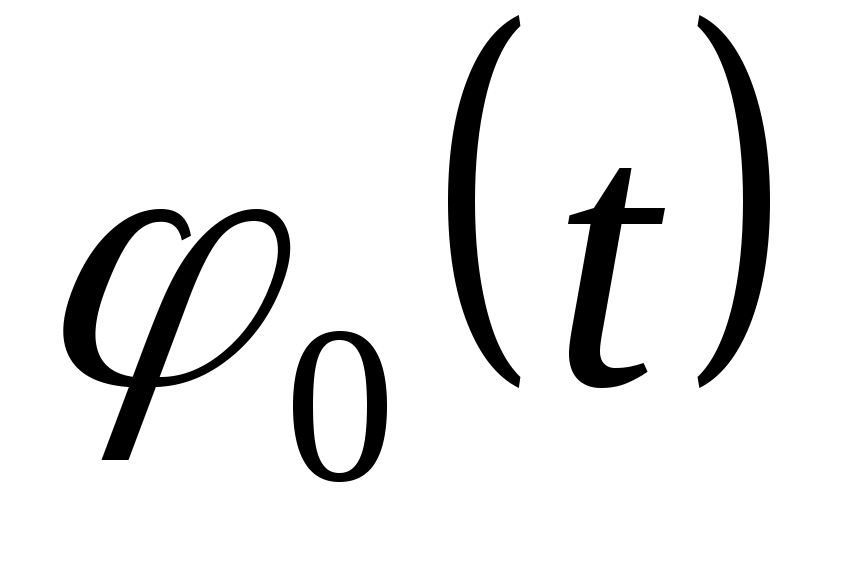 определяются по таблицам плотности нормированного и центрированного распределения, например, по [15, табл.1.1.]. определяются по таблицам плотности нормированного и центрированного распределения, например, по [15, табл.1.1.].
Дополнительные сведения о логарифмически нормальном распределении можно найти в [3,с.207; 6,с.54; 14; 15,с.75 и 157; 20,с.160; 21, с.431].
10.2.3. Распределение Рэлея
Распределение Рэлея относится к семейству однопараметрических распределений. Плотность и функция распределения определяются по формулам, если 0<x<:
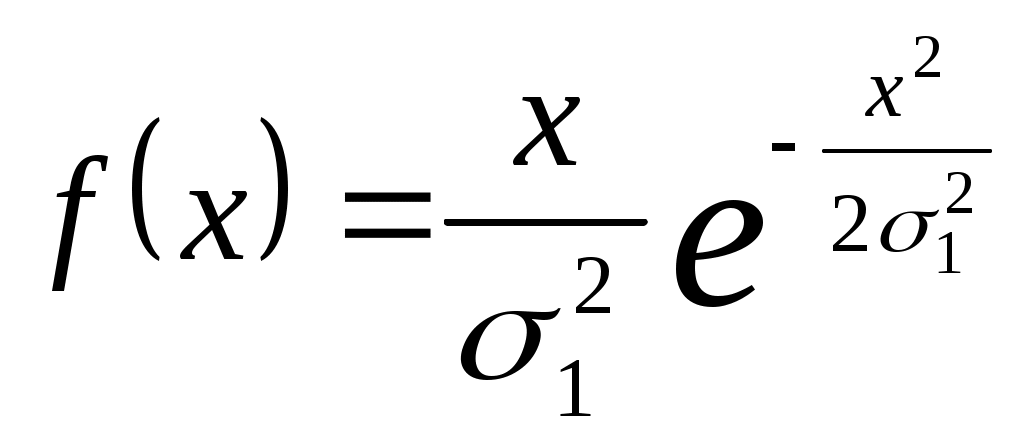 , ,
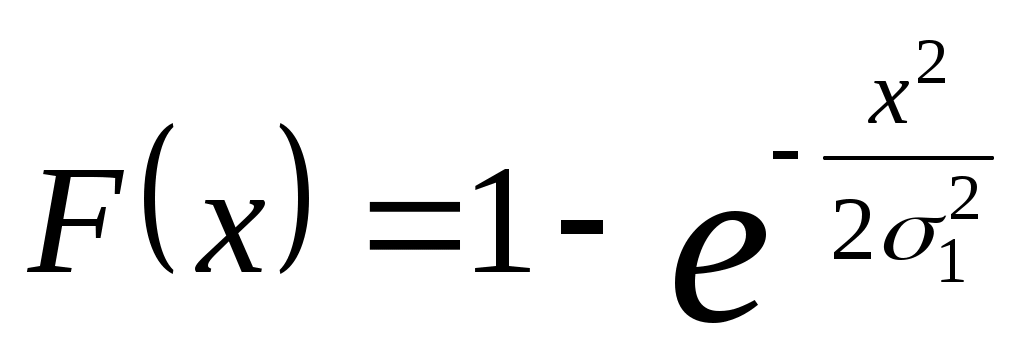 , ,
где 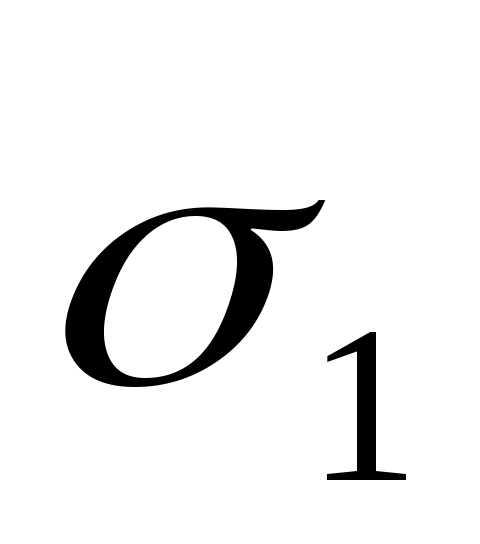 - параметр распределения. - параметр распределения.
Определить параметр распределения можно по методу максимального правдоподобия. Функция правдоподобия имеет вид
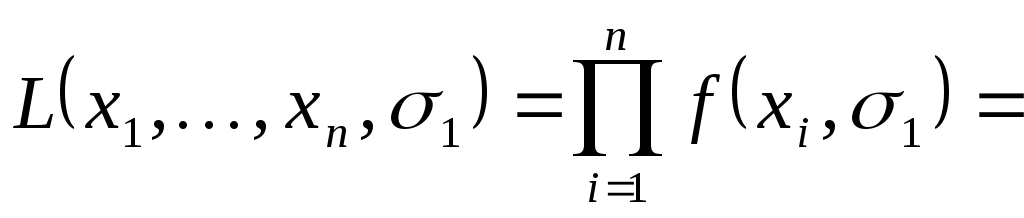
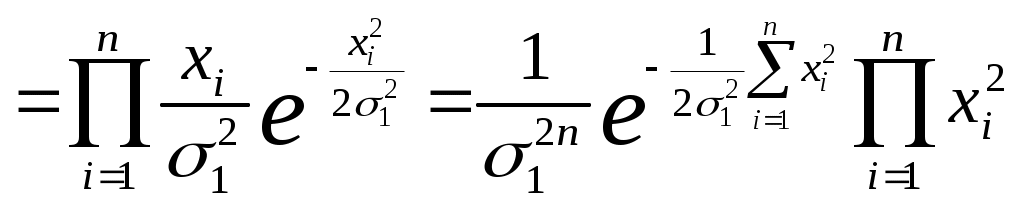 . .
Логарифмируем полученное выражение
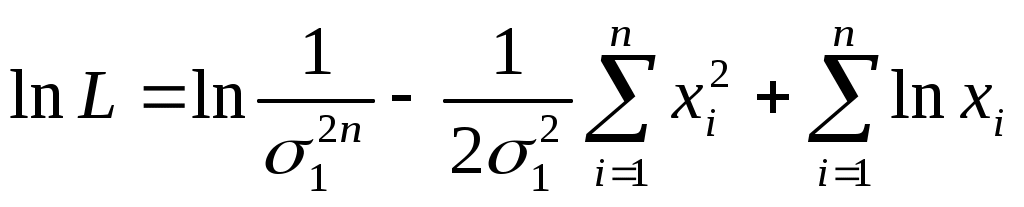 . .
Находим частную производную и приравниваем ее нулю
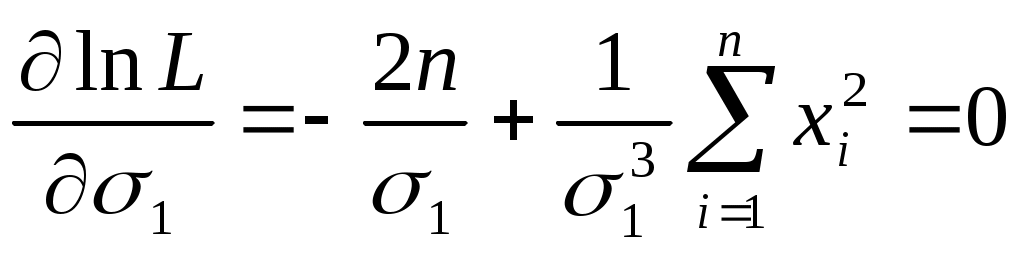 . .
Отсюда оценка параметра распределения равна
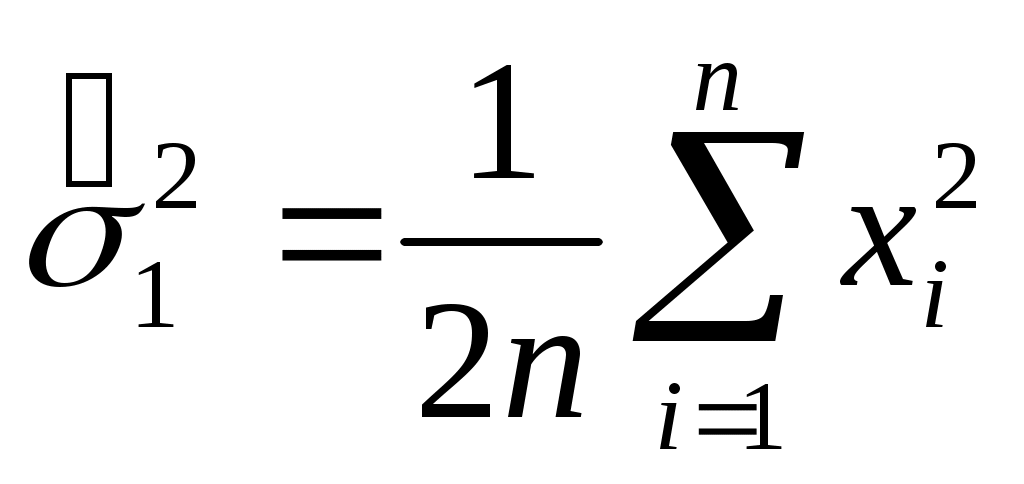 . .
Если использовать метод моментов, то
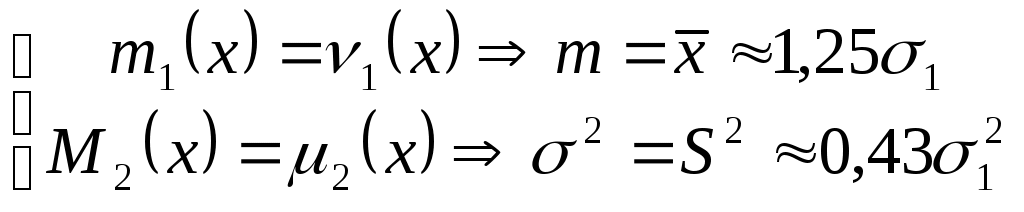
Откуда оценки параметра распределения получаются следующие:
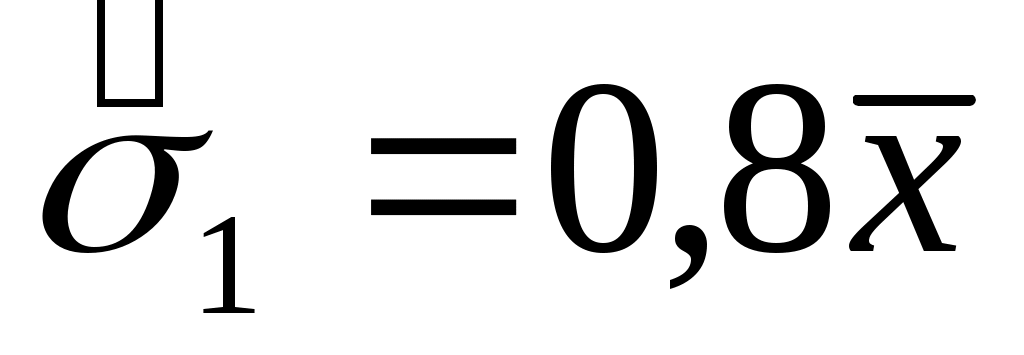 или или 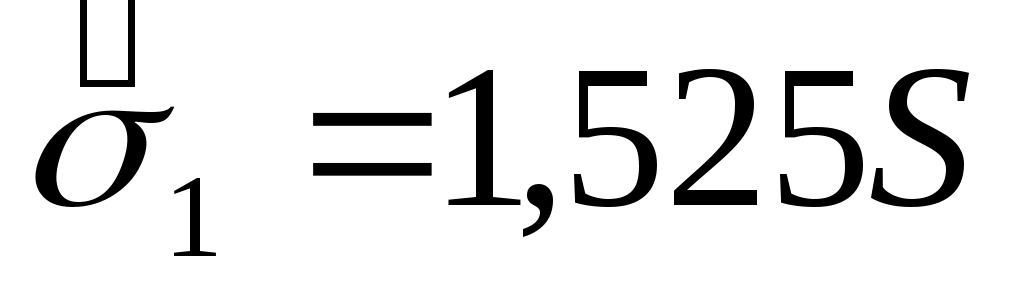 . .
Связь между m и 1 устанавливается выражением
1=0,524m.
Если распределение Рэлея начинается не с нуля, а меняется в пределах от b до , где 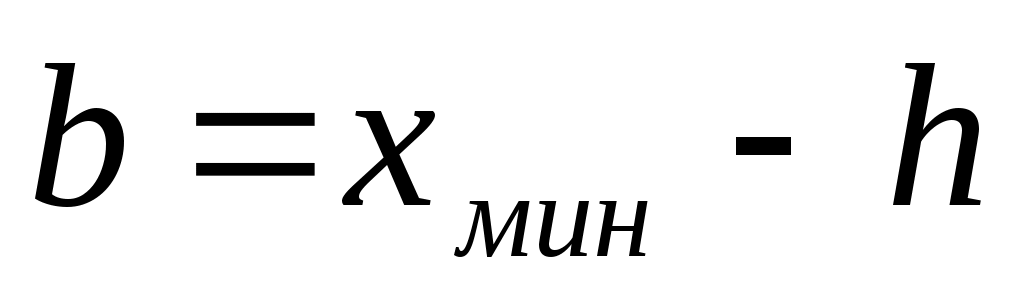 (сдвинутое распределение Релея), то для расчетов следует использовать выражения (сдвинутое распределение Релея), то для расчетов следует использовать выражения
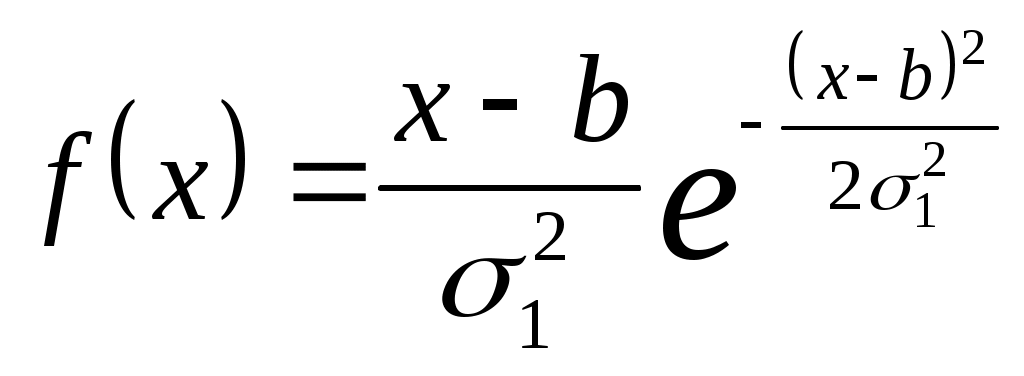 , ,
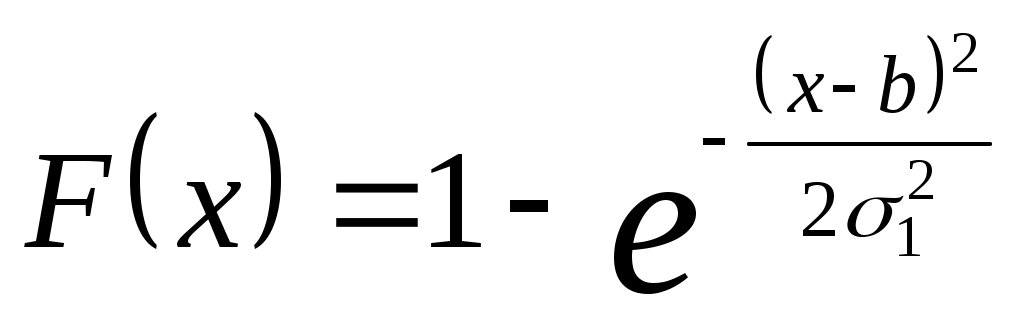 , ,
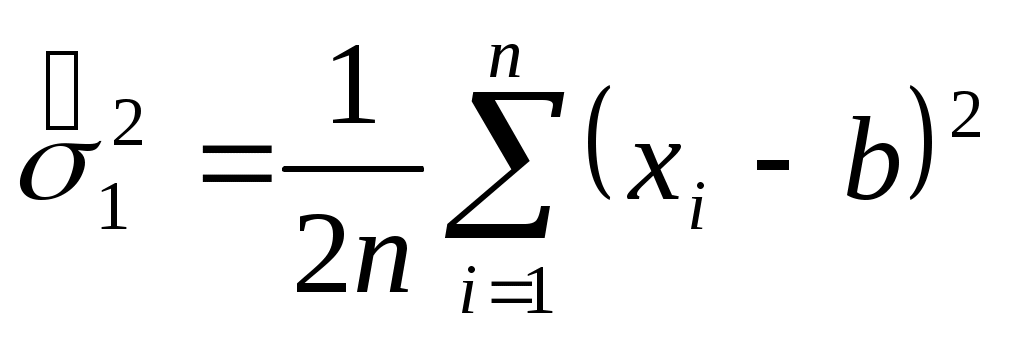 . .
При этом расчет 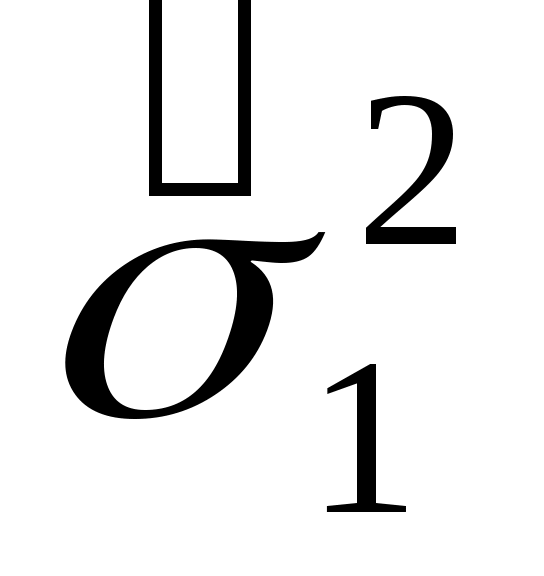 следует вести по вариационному ряду. Для интервального и дискретного рядов используются выражения следует вести по вариационному ряду. Для интервального и дискретного рядов используются выражения
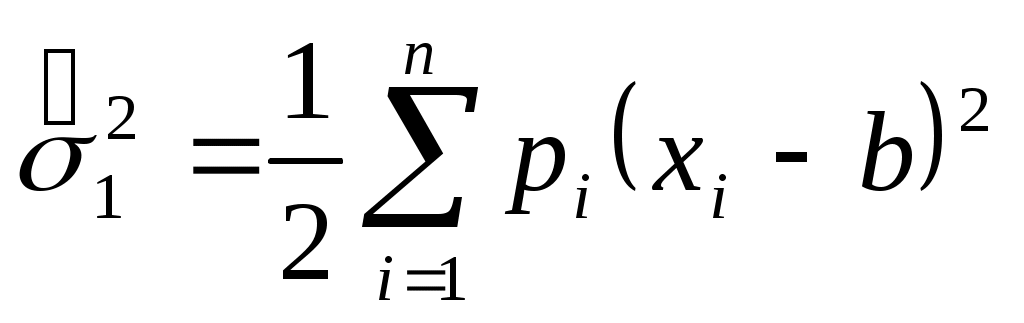 или или 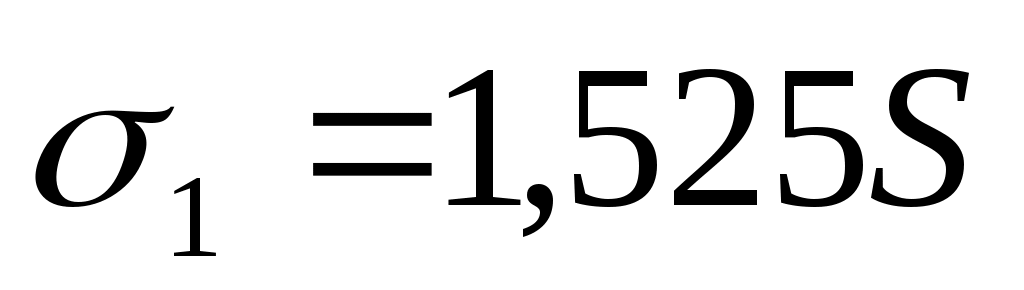 . .
Если эмпирическое распределение имеет левостороннюю асимметрию, то для его расчетов можно использовать распределение Рэлея с так называемым обращенным аргументом, которое лежит в пределах от - до d, где 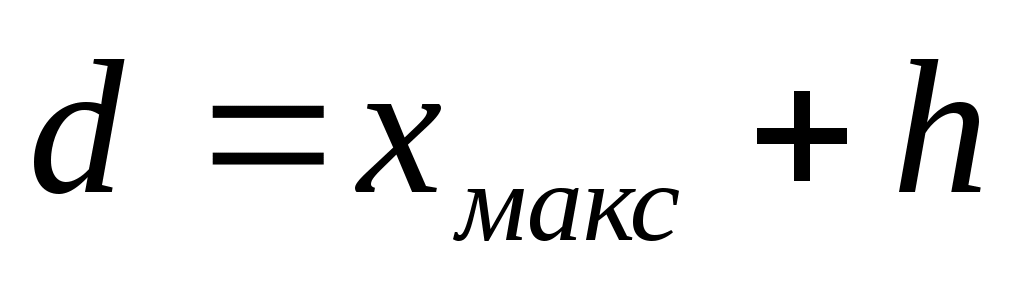 . Используются следующие формулы: . Используются следующие формулы:
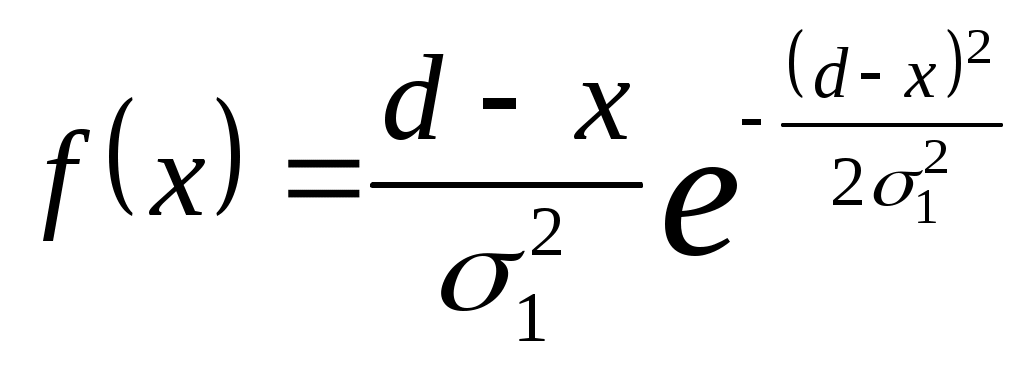 ; ;
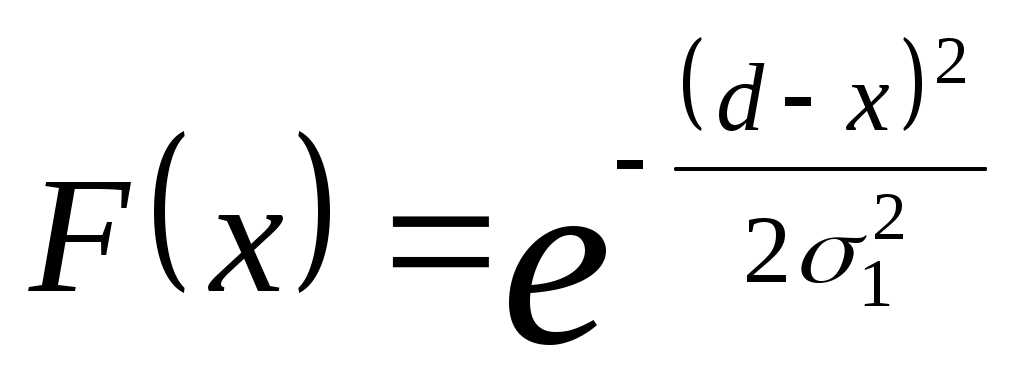 ; ;
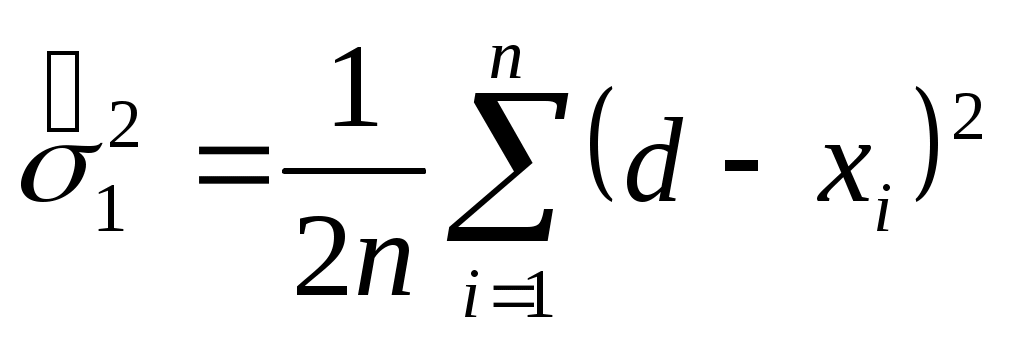 . .
При этом расчет 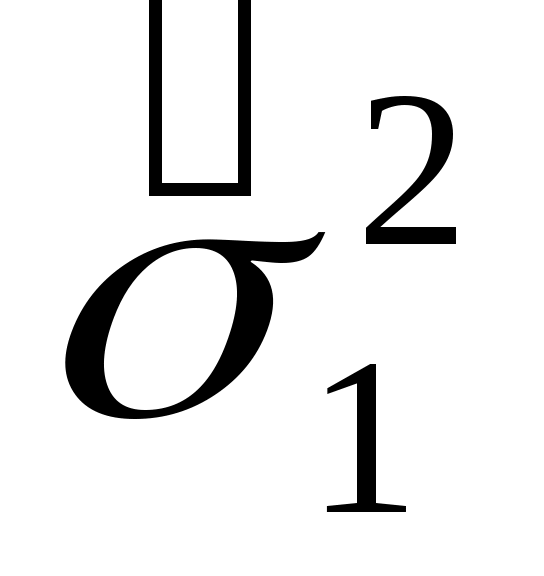 также ведется по вариационному ряду. Для интервального и дискретного рядов также ведется по вариационному ряду. Для интервального и дискретного рядов
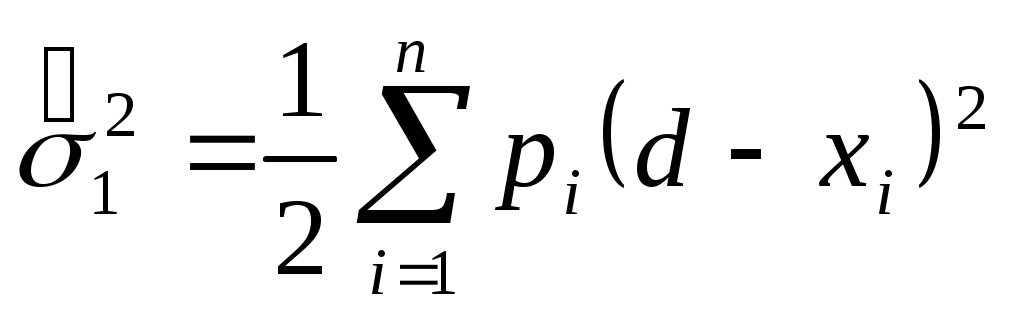 . .
Если для случая 0<x< мода равна 0=1, то для случая -<x<d мода равна 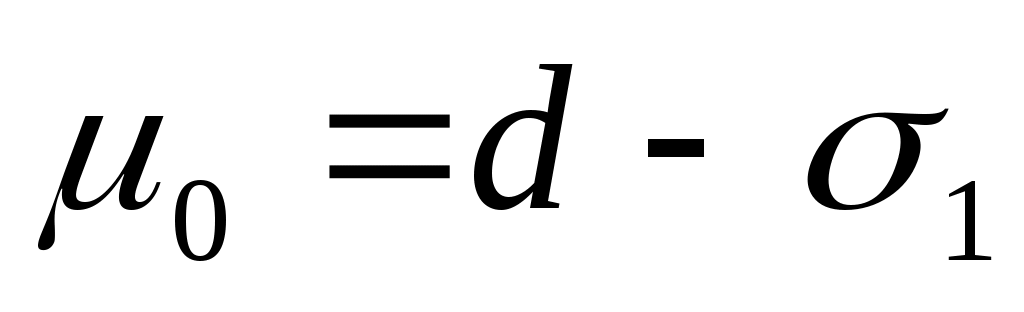 . Для обоих случаев . Для обоих случаев
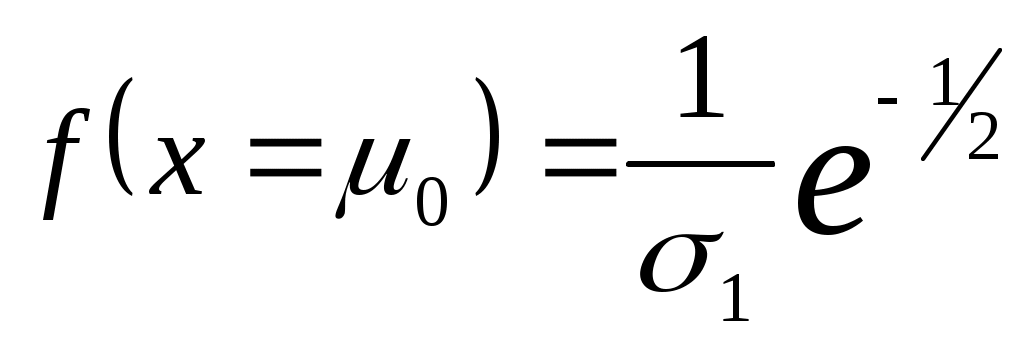 . .
Дополнительные сведения о распределении Рэлея можно найти в [21, с.432; 22,с.36].
10.2.4. Некоторые другие распределения, отличные от
нормального
В связи с ограниченным объемом данного пособия, укажем лишь литературу для некоторых распределений.
Сведения об определении параметров распределений методом моментов или методом максимального правдоподобия, а также формулы для расчетов плотности и функции распределения и различных моментов можно найти:
- для экспоненциального распределения в [3,с.219; 10,с.34 и 38; 15,с.154; 20,с.170; 21,с.417; 22,с.35];
- для усеченного экспоненциального распределения в [15,с.120];
- для сдвинутого экспоненциального распределения в [34,с.90];
- для распределения Вейбулла в [3,с.223 и 393; 14; 15,с.39 и 155; 20,с.177; 21,с.425; 22,с.38; 24,с.235; 27,с.14; 33];
- для гамма-распределения в [3,с.212; 9,с.247 и 255; 15,с.67; 20,с.163; 21,с.424; 22,с.39; 23,с.504; 24,с.228];
- для распределения Эрланга в [21,с.422; 22,с.37];
- для распределения Максвелла в [21,с.434];
- для бэта-распределения в [9,с.250 и 257].
Многочисленные распределения типа 1-VII (римская 7) (кривые Пирсона) приведены в [9,с.273].
Указанные распределения могут иметь также левостороннюю (отрицательную) асимметрию, что требует их использования с обращенным аргументом.
11. ПРОВЕРКА ПРАВИЛЬНОСТИ ВЫБОРА ТЕОРЕТИЧЕСКОГО ЗАКОНА
|
 Скачать 1.66 Mb.
Скачать 1.66 Mb.
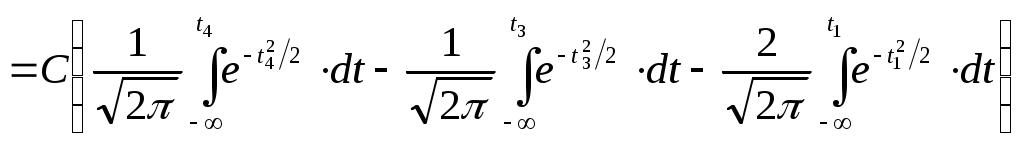 ,
,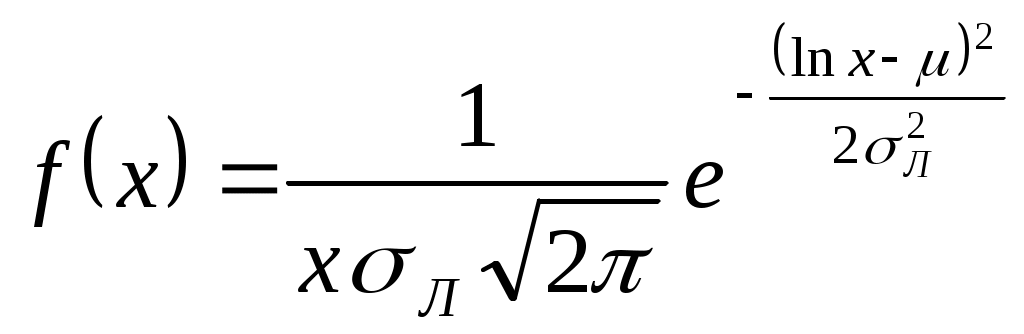 ;
;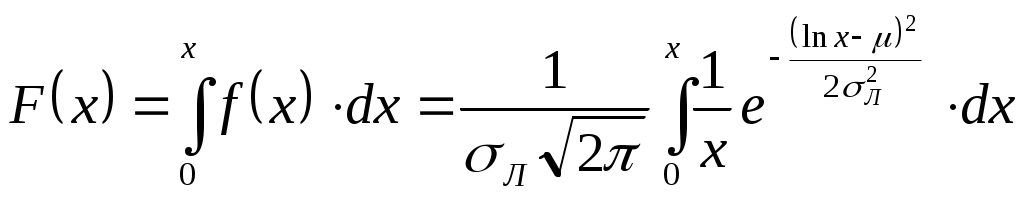 .
.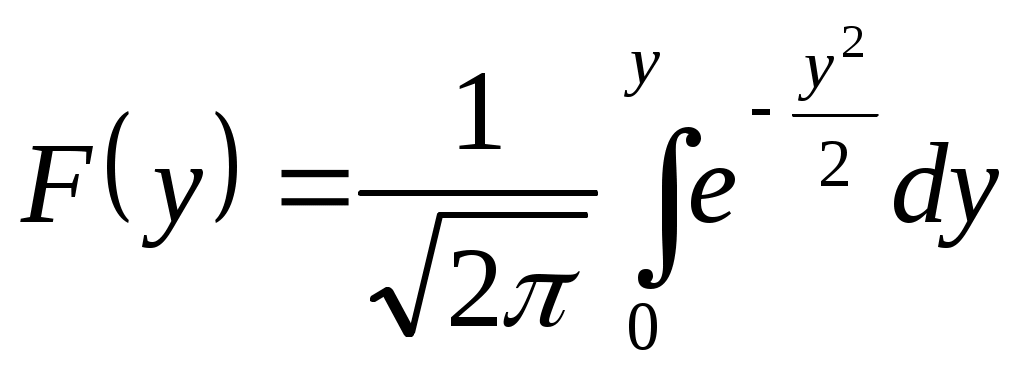 находим по y в [15, табл. 1.2].
находим по y в [15, табл. 1.2].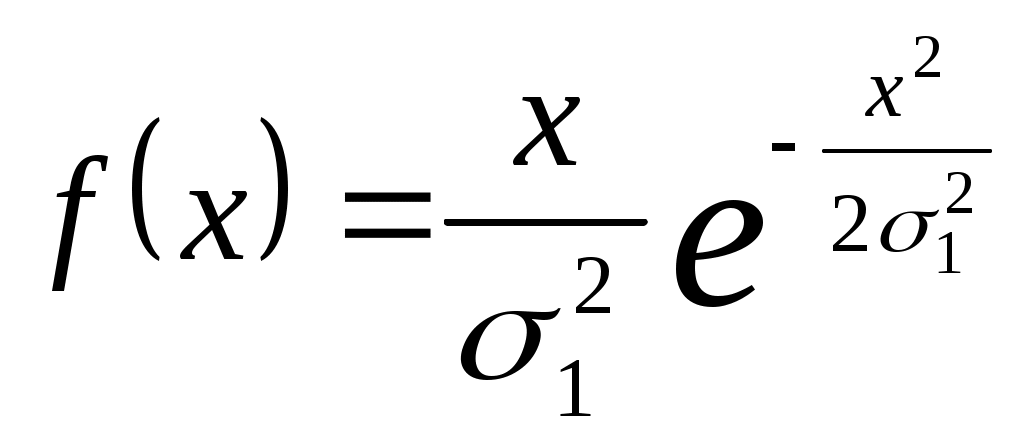 ,
,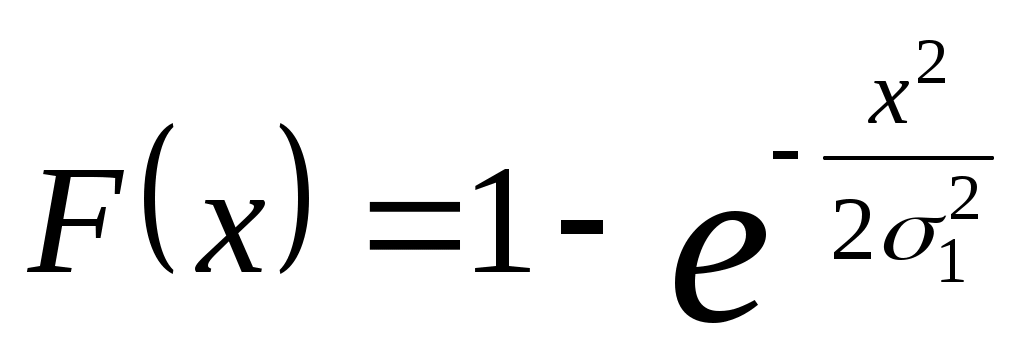 ,
,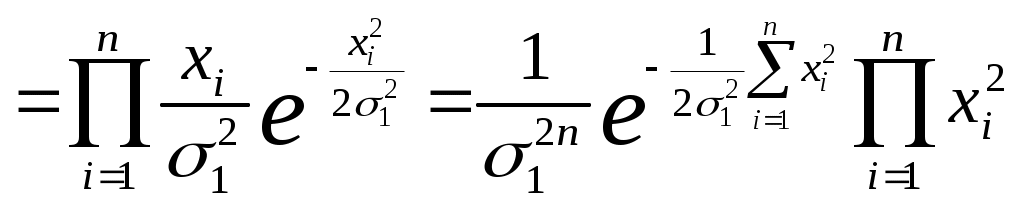 .
.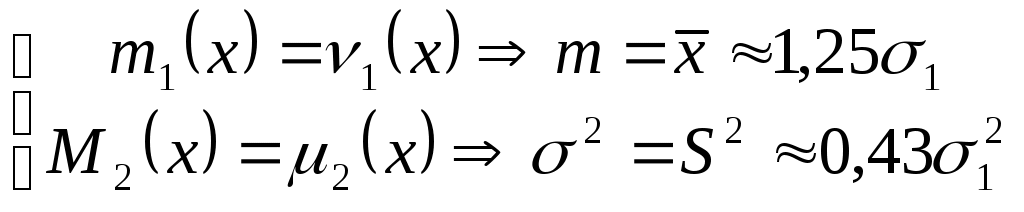
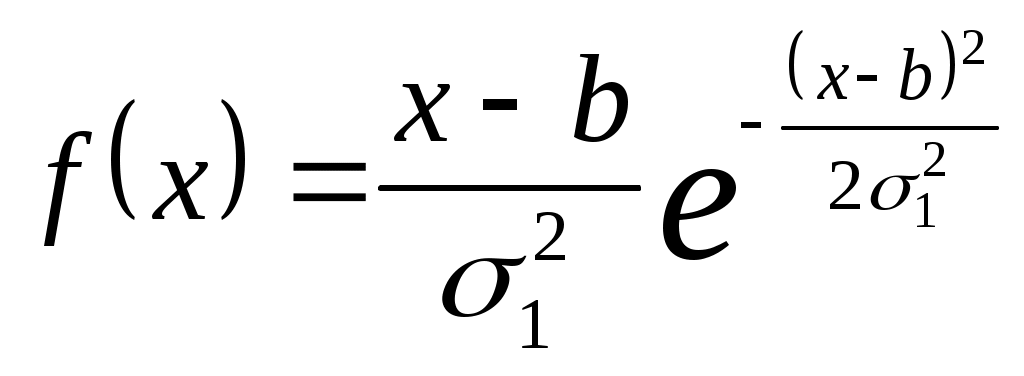 ,
,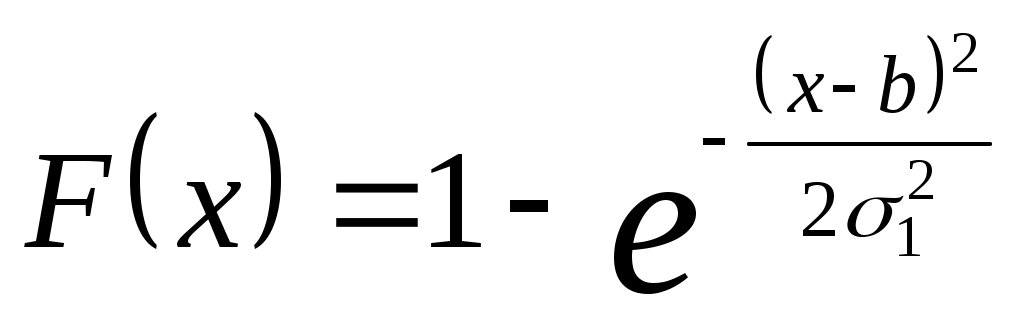 ,
,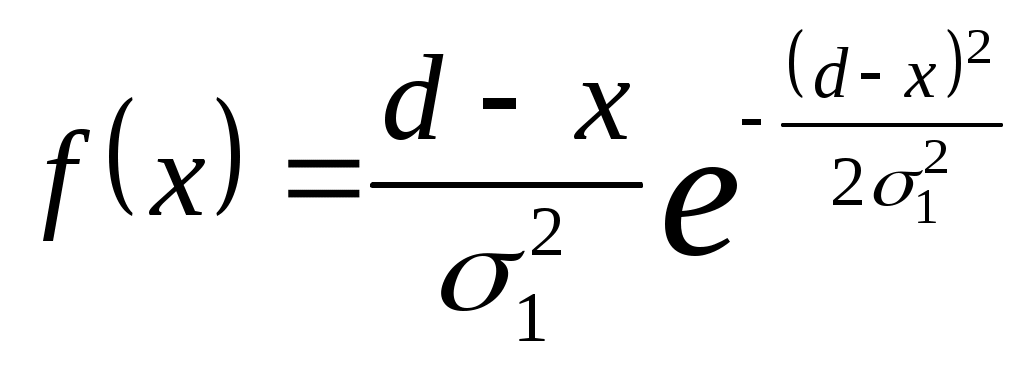 ;
;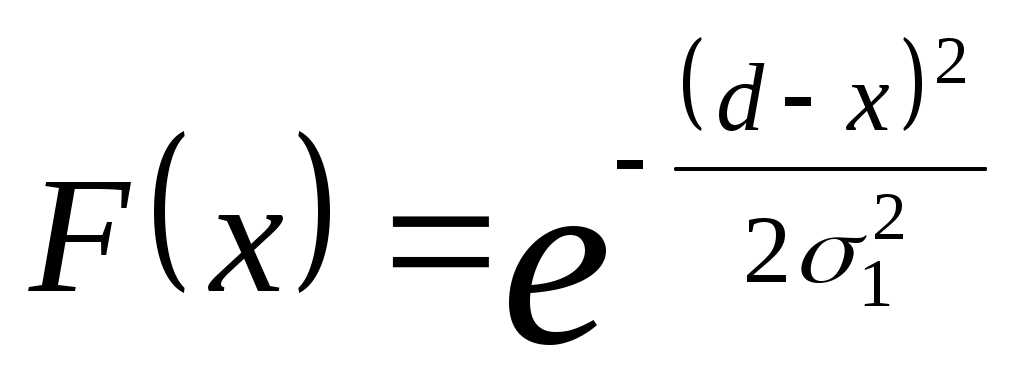 ;
;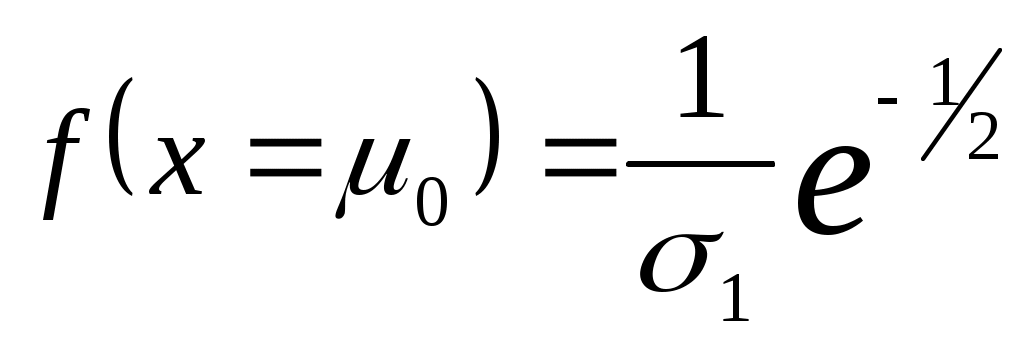 .
.