Системы поддержки принятия решения

• Название: Системы поддержки принятия решения
• Дата: 27.02.2023
• Размер: 3.85 Mb.
• Имя файла: Metodichka_SPPRLR240408.doc
• Тип: Методическое пособие; #957823
• страница: 11 из 28

Игры с противником.

Рассмотрим задачу разработки управленческого решения с одним неопределенным фактором 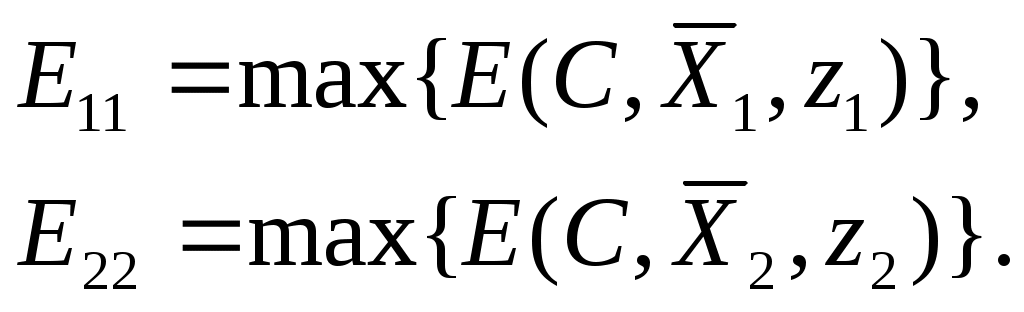, принимающим только два возможных значения при выборе противником соответственно стратегий и . Заметим, что хотя мы не знаем, какие конкретно значения на практике будут принимать неопределенные факторы, но мы можем предположить, что они примут определенные значения и вести дальнейшие рассуждения в отношении именно предполагаемых нами значений . Будем считать, что этот фактор влияет на критериальную функцию или на ограничения . Найдем два оптимальных решения и , с учетом двух возможных и предполагаемых нами стратегий противника и соответствующие выражениям



Полученные решения и представляют собой наши наилучшие действия (стратегии) и в том случае, когда мы угадали дальнейшее развитие событий. Используя уже полученные решения и , рассчитаем значения показателя эффективности при условии, что мы не угадали ответ противника:



Занесем полученные значения в так называемую платежную матрицу, где строки и представляют собой наши возможные стратегии, а столбцы и возможные стратегии противника

Стратегии

Очевидно, что аналогичная матрица может быть построена и при большем числе возможных стратегий , а также при большем числе неопределенных факторов .

Отыщем решение игры, пользуясь методами теории игр. Найдем нашу оптимальную стратегию, не зависящую от действий противника. В этом случае возникает вопрос о выборе критерия оптимальности. Например, в качестве используемой стратегии можно выбрать стратегию, которая приносит возможный максимальный выигрыш. Такая стратегия может оказаться весьма рискованной, поскольку в конкретной ситуации противник может ответить стратегией, приводящей к большему проигрышу. Более разумным представляется воспользоваться стратегией, которая минимизирует наш возможный проигрыш. Обозначим минимальный выигрыш при выборе стратегии при всех возможных стратегиях противника

.

Из всех возможных наших стратегий выберем стратегию, которая обеспечит нам наибольшее значение нашего минимального выигрыша

.

Назовем нижней ценой игры (наш гарантированный выигрыш при любой стратегии противника).

Если цели игроков противоположны, что имеет место в антагонистической игре, то противник заинтересован уменьшить наш выигрыш, и будет выбирать соответствующие стратегии. Вполне естественно предположить, что противник владеет методами оптимизации и теории игр и в свою очередь проводит аналогичные вычисления. Тогда полученная им платежная матрица будет иметь другие числовые значения, но ее смысл в отношении выбираемых стратегий не изменится. Поэтому мы можем анализировать возможные стратегии противника исходя из имеющейся у нас нашей платежной матрицы. Очевидно, что все это справедливо только в том случае, когда мы рассмотрели все возможные стратегии противника.

Примечание. Если противник не будет пользоваться оптимальными методами, то это просто приведет к его дополнительному проигрышу.

Найдем наш максимальный выигрыш при каждой стратегии противника

.

Для того чтобы минимизировать свой проигрыш, противник выберет стратегию, в которой наш выигрыш минимален

.

Назовем выигрыш верхней ценой игры. Очевидно, что если по каким-то причинам противник не воспользовался своей оптимальной стратегией, то наш выигрыш только возрастет. Если верхняя и нижняя цены игры совпадают, то их значение называют чистой ценой игры

.

Стратегии, соответствующие чистой цене игры, называются чистыми, а их совокупность дает оптимальное решение. Используя оптимальное решение, мы получаем минимальный гарантированный выигрыш независимо от поведения противника. Пара чистых стратегий и дает оптимальное решение игры тогда и только тогда, когда соответствующий им элемент является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация называется седловой точкой, а соответствующая ей игра - игрой с седловой точкой.

Если седловая точка в платежной матрице отсутствует, то существует несколько наших чистых стратегий и стратегий противника, позволяющих получить цену игры. Выбор нами одной из стратегий наталкивается на естественное противодействие противника, желающего минимизировать свой проигрыш и выбирающего ответную стратегию с учетом информации о нашем выборе. Это обстоятельство приводит к тому, что мы вынуждены хранить свой выбор в тайне и, кроме этого, чередовать свои стратегии при многократном повторении игры по случайному закону. Если так не делать, то противник привыкнет к тому, что мы играем одинаково, и с учетом этого будет строить свою игру. Смешанной стратегией называется применение стратегий , ,..., с вероятностями , ,…, , причем

. (8)

Будем записывать смешанные стратегии в виде матрицы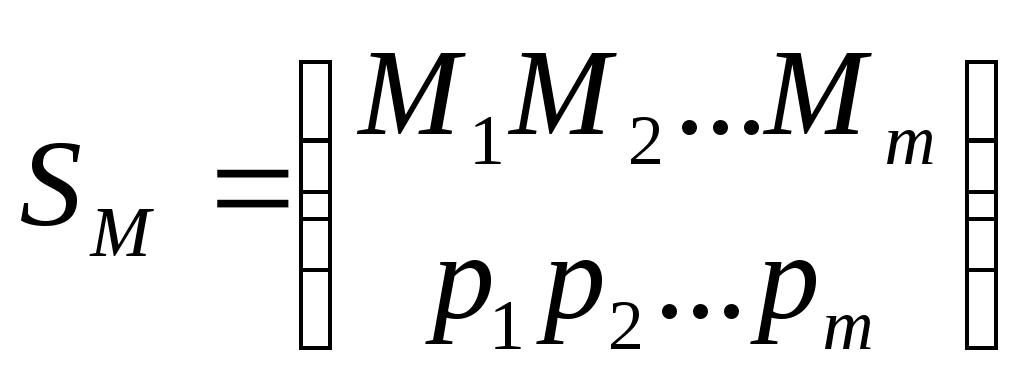

,

или в виде вектора 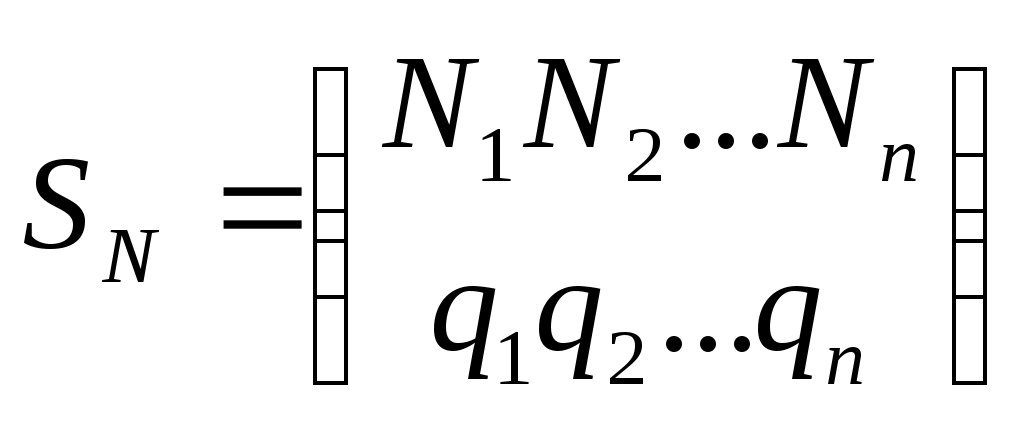. Смешанные стратегии противника запишем аналогично, обозначая соответствующие вероятности буквой :

,

,

или . Найдем оптимальную стратегию , обеспечивающую нам средний выигрыш не меньший, чем цена игры ( ). Математическое ожидание нашего выигрыша при реализации противником стратегии

.

Если - цена игры, то при условии имеем набор ограничений

.

Учитывая (1)), будем искать набор 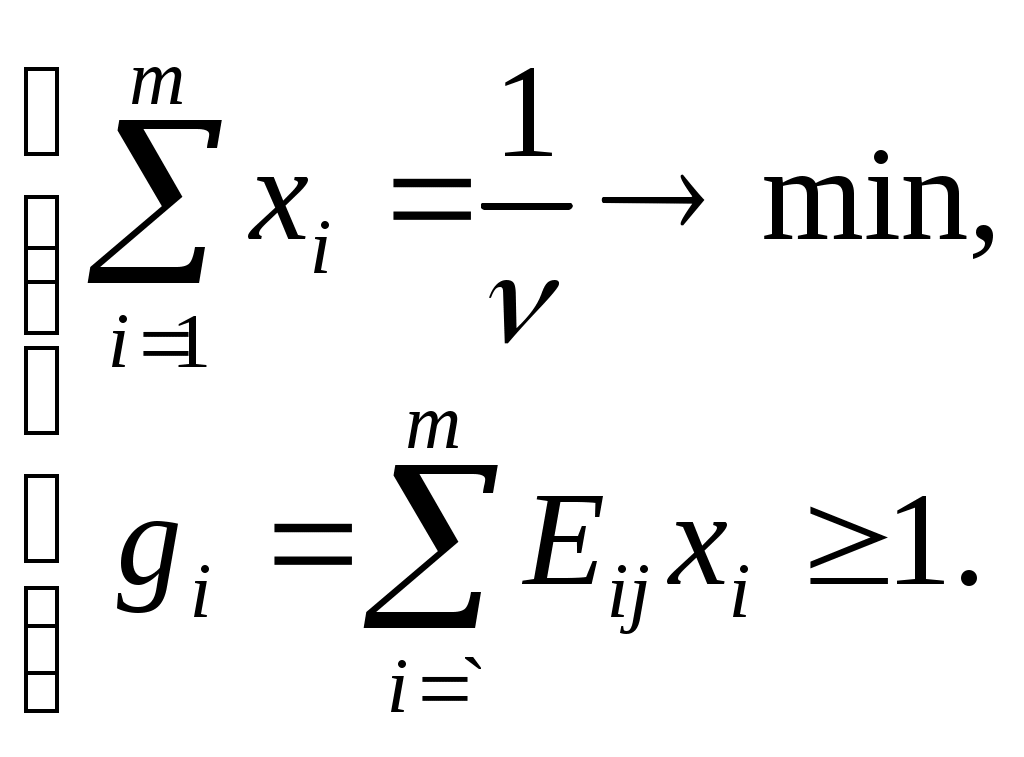, обеспечивающий максимальную цену игры , для чего сделаем замену переменных . Запишем итоговые выражения для целевой функции и ограничений задачи оптимизации выбора стратегий



и решим задачу линейного программирования. Элементы нашей оптимальной смешанной стратегии 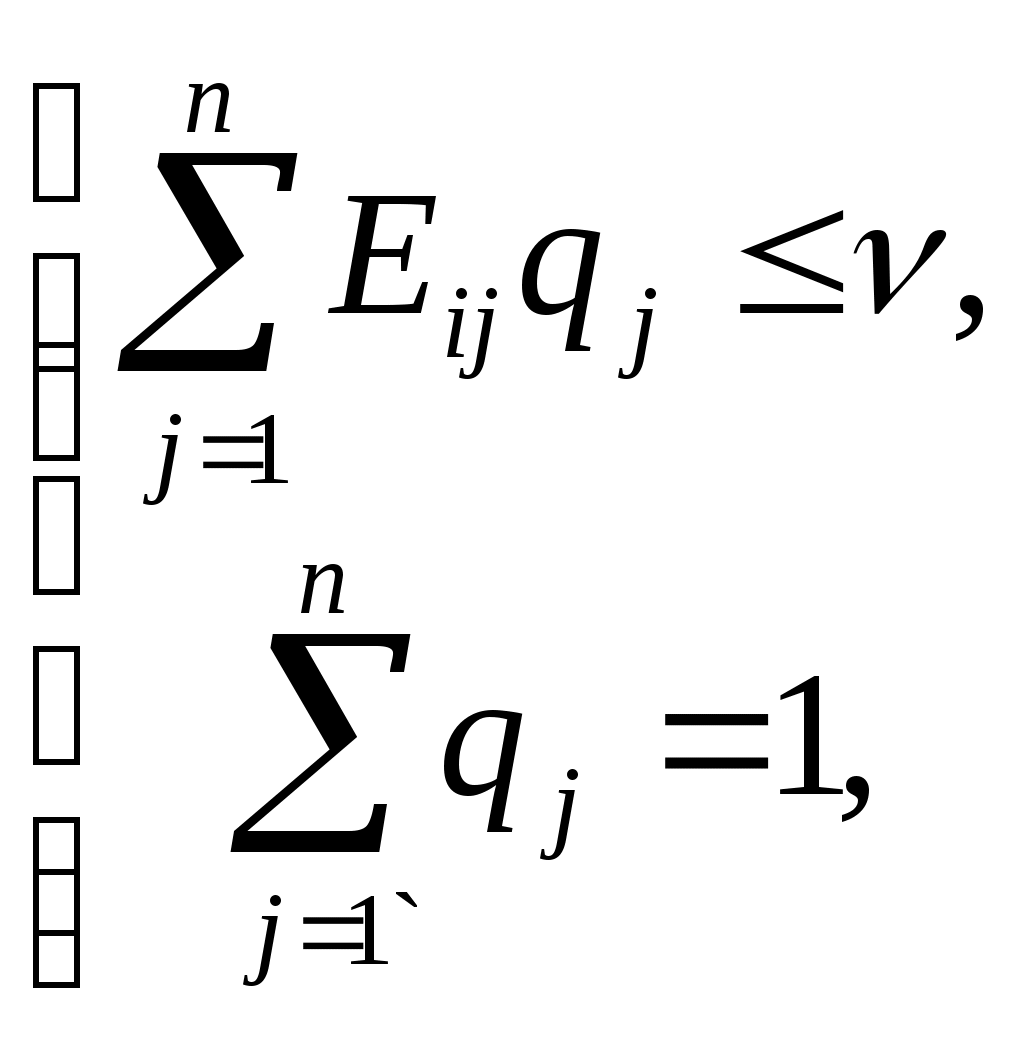определяются подстановкой . Оптимальная смешанная стратегия противника определяется аналогично:



а задача линейного программирования формулируется в виде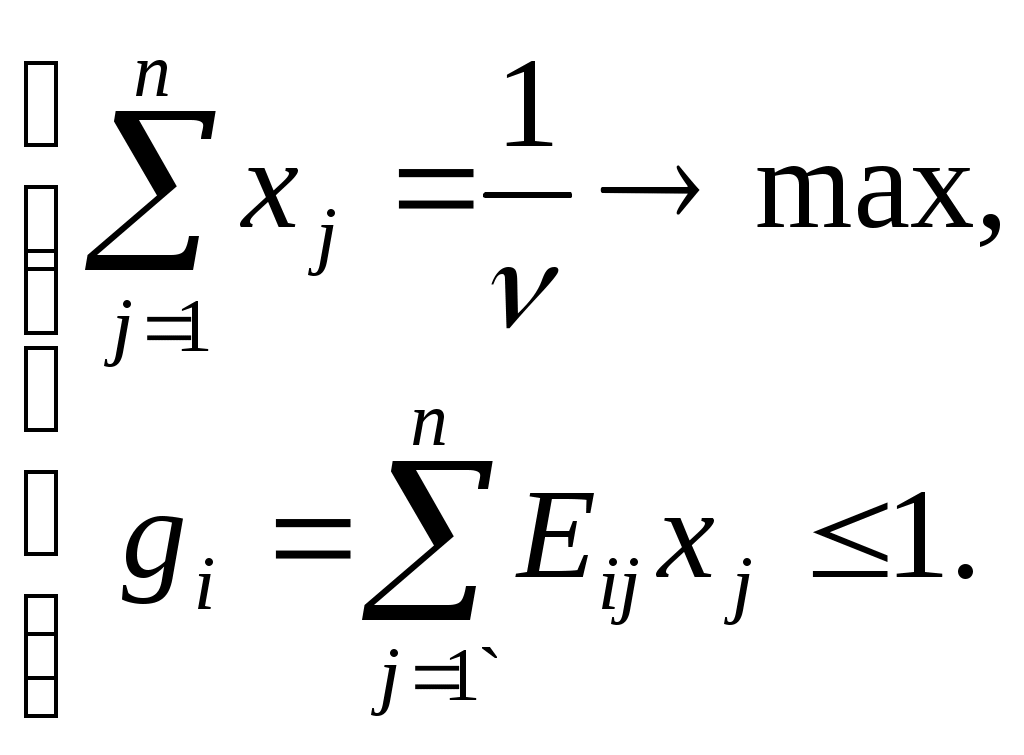



Тогда результатом решения задачи разработки управленческого решения будет последовательность наших стратегий, реализуемых по случайному закону с заданными вероятностями их появления.

Лабораторная работа №6. Решение однокритериальной статической задачи в условиях неопределенности при играх с противником

Задание

Используйте придуманную вами задачу разработки управленческого решения. Задайтесь параметром, который может быть в условиях неопределенности в результате возможных действий противника. Рассматривайте случай дуальной игры с противником с нулевой суммой и решите задачу.

Порядок выполнения работы

1. 
   Из общего числа параметров вашей задачи разработки управленческого решения выберите один, который будет рассматриваться в условиях неопределенности. Согласуйте с преподавателем выбранный вами параметр.
   
2. 
   На основе анализа ситуации в зависимости от возможных действий противника задайтесь возможными значениями случайного параметра , для которых будет делаться расчет. Каждое значение этого параметра будет определять одну из наших стратегий и одну из возможных стратегий противника.
   
3. 
   Решая задачу с помощью надстройки Поиск решения, определите значение критериальной функции и соответствующие ему решения в предположении, что стратегия противника угадана, то есть мы предполагаем значение параметра , и в результате действий противника он принимает именно такое значение.
   
4. 
   Постройте платежную матрицу, заполните ее диагональ значениями и отдельно запишите соответствующие им решения .
   
5. 
   Используя выражение для показателя эффективности, рассчитайте значения критериальной функции в предположении, мы используем стратегию , то есть решение , а в результате действий противника параметр принимает значение .
   
6. 
   Заполните значениями свободные клетки платежной матрицы.
   
7. 
   Просматривая колонки платежной матрицы ( ), найдите для каждой строки наш гарантированный минимальный выигрыш .
   
8. 
   Найдите номер нашей стратегии, обеспечивающей нам максимум гарантированного выигрыша (нижнюю цену игры) .
   
9. 
   Просматривая строки платежной матрицы ( ), найдите для каждого столбца гарантированный максимальный проигрыш противника (верхнюю цену игры) .
   
10. 
    Найдите номер стратегии противника, обеспечивающей ему минимум гарантированного выигрыша .
    
11. 
    Сравните верхнюю и нижнюю цены игры и определите факт наличия или отсутствия седловой точки.
    
12. 
    Если седловая точка существует ( ), то определите оптимальное решение задачи соответствующее номеру чистой стратегии, обеспечивающей .
    
13. 
    Если седловая точка отсутствует ( ), то определите набор своих стратегий , которые обеспечивают значение , имеют свой выигрыш и будут чередоваться нами в случайном порядке. Аналогично определите набор стратегий противника . Сформируйте новую матрицу размером , элементы которой представляют выборку из платежной матрицы в соответствии с принятыми в рассмотрение стратегиями.
    
14. 
    Отдельно сформулируйте и решите еще одну задачу линейного программирования, принимая во внимание 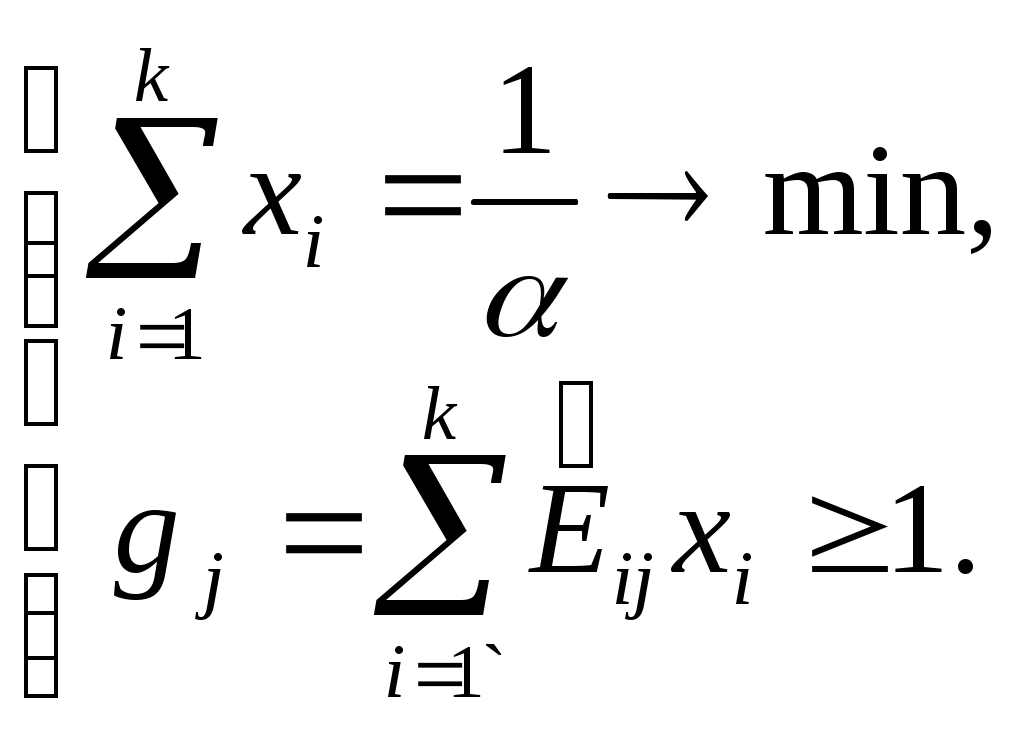ограничений
    

15. 
    В соответствии с полученным решением по формуле определите набор вероятностей , с которыми необходимо чередовать стратегии .
    

Контрольные вопросы

1. 
   Чем задача в условиях неопределенности отличается от задачи в условиях риска?
   
2. 
   Что такое стратегия?
   
3. 
   Что такое дуальная игра?
   
4. 
   В каком случае игра может называться игрой с нулевой суммой?
   
5. 
   В каком случае игра классифицируется как игра с противником?
   
6. 
   Как составляется платежная матрица?
   
7. 
   Чем элементы диагонали платежной матрицы отличаются от других элементов?
   
8. 
   Что такое седловая точка?
   
9. 
   В каком случае седловая точка может отсутствовать?
   
10. 
    Что такое нижняя и верхняя цены игры?
    

Отчет о работе

Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите обоснование выбора его значений. Представьте платежную матрицу и результаты ее обработки. Определите факт наличие или отсутствия седловой точки. Если она существует, то приведите результаты решения задачи. Если седловой точки нет, то приведите набор стратегий, взятых в рассмотрение, представьте формулировку и результаты решения задачи определения набора вероятностей, с которыми будут чередоваться стратегии, и поставьте каждой в соответствие решение. Сформулируйте выводы, которые можно сделать по результатам выполненной работы.

Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б.

Игры с природой.

Отличительной особенностью игр с природой является то обстоятельство, что природа рассматривается как некоторая незаинтересованная инстанция, поведение которой неизвестно, но, во всяком случае, не содержит элемента враждебности и сознательного противодействия достижению наших целей. Как и в случае игр с противником, нам должна быть известна платежная матрица, соответствующая нашему выигрышу при различных своих стратегиях и состояниях (стратегиях) природы. Если в случае игры с противником предполагать определенные вероятности появления его стратегий не представлялось возможным, то в рассматриваемой ситуации нам полезно дополнительно располагать информацией о вероятностях появления возможных состояний природы, заданной, например, в виде смешанных стратегий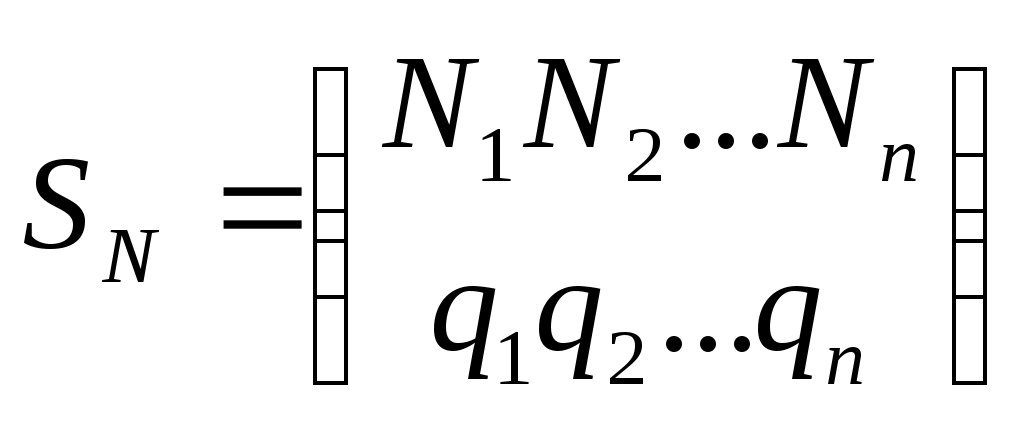

,

.

Задача заключается в выборе в конкретных условиях наиболее выгодной собственной стратегии, а отбрасывать «невыгодные» с точки зрения природы стратегии нельзя. Исходя из этого в теории статистических решений [3] вводится понятие риска

,

где наш риск при использовании стратегии в ответ на состояние природы , а - максимально возможный наш выигрыш при состоянии природы . Если нам известны вероятности возможных состояний природы , то было бы логичным в качестве своей стратегии принять одну из наших возможных стратегий , максимизирующую наш средний выигрыш

.

Отметим, что указанная стратегия одновременно минимизирует средний риск.

Примечание. В случае игры с природой количество наших возможных стратегий может отличаться от количества возможных стратегий природы .

При выборе оптимальной стратегии одну из существенных трудностей представляет определение конкретного набора вероятностей . Если нет никаких гипотез о вероятности появления определенного состояния природы, то используется принцип недостаточного основания Лапласа, когда вероятности назначаются равными друг другу

.

Если у нас существуют некоторые предположения о вероятностях появления определенных событий, то мы можем их расставить в порядке убывания их правдоподобности (ранжировать) и поставить им в соответствие некоторый ряд чисел, определенный, в том числе, и экспертным путем. Отметим, что в любом случае справедливо утверждение

.

Лабораторная работа №7. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой

Задание

Используйте придуманную вами задачу разработки управленческого решения. Задайтесь параметрами, которые могут быть в условиях неопределенности. Рассмотрите случай игры с природой и решите задачу.

Порядок выполнения работы

1. 
   Из общего числа параметров вашей задачи разработки управленческого решения выберите один, который будет рассматриваться в условиях неопределенности. Согласуйте с преподавателем выбранный вами параметр.
   
2. 
   На основе анализа ситуации в зависимости от возможных воздействий природы задайтесь возможными значениями случайного параметра , для которых будет делаться расчет. Каждое значение этого параметра будет определять одну из наших возможных стратегий
   
3. 
   Из числа значений случайного параметра задайтесь ( ) возможными значениями, которые определяют возможные стратегии природы и вероятности их появления , обеспечив выполнение условия
   

.

4. 
   Решая задачу с помощью надстройки Поиск решения, определите значение критериальной функции и соответствующие ему решения в предположении, что стратегия природы угадана, то есть мы предполагаем значение параметра , и в результате действий природы он принимает именно такое значение.
   
5. 
   Постройте платежную матрицу, заполните ее диагональ значениями и отдельно запишите соответствующие нашим стратегиям решения .
   
6. 
   Используя полученное решение для каждой строки подставляя соответствующее стратегии природы значение параметра в выражение для критериальной функции рассчитайте остальные элементы платежной матрицы .
   
7. 
   В соответствии с максиминным критерием Вальда выберите стратегию, гарантирующая выигрыш не меньший, чем
   

.

8. 
   Определите наш максимальный выигрыш при каждой стратегии природы и рассчитайте матрицу риска в соответствии с выражением
   

9. 
   В соответствии с критерием минимаксного риска Сэвиджа определите стратегию, обеспечивающую минимальный риск
   

.

10. 
    Задайтесь несколькими значениями ( ) и выберите стратегии в соответствии с критерием пессимизма-оптимизма Гурвица
    

.

11. 
    Сравните результаты расчетов и принятые решения при использовании критериев Вальда, Сэвиджа и Гурвица при различных .
    

Контрольные вопросы

1. 
   Чем игры с природой отличаются от игр с противником?
   
2. 
   Почему при играх с природой можно задавать значения вероятностей возникновения стратегий природы?
   
3. 
   Как можно определить вероятность возникновения стратегии природы?
   
4. 
   Чем матрица риска отличается от платежной матрицы?
   
5. 
   В чем заключается разница между критерием Вальда и критерием Сэвиджа?
   
6. 
   В чем заключается разница между критерием Вальда и критерием Гурвица?
   
7. 
   Почему игры с природой оказываются сложнее игр с противником?
   
8. 
   Что общего и в чем отличие методик разработки управленческого решения при играх с противником и играх с природой?
   
9. 
   Что такое смешанная стратегия?
   
10. 
    Из каких соображений следует выбирать параметр критерия Гурвица?
    

Отчет о работе

Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите обоснование выбора его значений. Представьте платежную матрицу и результаты ее обработки. Укажите решение, полученное при использовании критерия Вальда. Представьте матрицу риска и укажите решение, полученное при использовании критерия Сэвиджа. Приведите результаты решения задачи с использованием критерия Гурвица. Покажите зависимость принятого решения от значения параметра критерия Гурвица. Сформулируйте выводы, которые можно сделать по результатам выполненной работы.

Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б.

Игры с природой с экспериментами.

Рассмотренные выше игры с природой предусматривали необходимость принятия нами решения в условиях неопределенности на основе имеющихся у нас данных, используемых в процессе вычислений. Такие данные принято называть априорными. В некоторых случаях при решении задач с природными неопределенностями появляется возможность проведения различных экспериментов, позволяющих получить дополнительную информацию и тем самым снизить степень неопределенности в отношении действительного состояния природы. Очевидно, что проведение экспериментов связано с затратой ресурсов. Возникают естественные вопросы: стоит ли проводить эксперимент, сколько должно быть экспериментов, в каком порядке надо проводить эксперименты. Некоторые ответы на эти вопросы дает теория игр с экспериментами.

Назовем единичным такой эксперимент, объем и порядок которого заранее определены и не могут быть изменены в процессе его проведения. Отметим, что собственно методику эксперимента должен разрабатывать специалист в предметной области, а мы можем только делать вывод о целесообразности его проведения на основании имеющейся априорной информации. Единичный эксперимент не обязательно состоит только из одного испытания. В процессе его проведения может быть получена целая выборка значений, однако принципиальным является то обстоятельство, что объем выборки конечен и известен заранее.

Возможен и другой способ организации эксперимента. В процессе проведения эксперимента после каждого испытания мы можем принимать решение, прекратить ли дальнейшие испытания и выбрать ли какую либо стратегию из числа возможных или продолжить испытания с целью увеличения объема информации. Такие эксперименты называют последовательными. Максимальное допустимое количество выборок в процессе проведения последовательного эксперимента тоже может быть известно заранее (в этом случае говорят об усеченном последовательном эксперименте), или быть неограниченным (неограниченный последовательный эксперимент).

Будем считать, что в нашем распоряжении имеется набор стратегий , которые он может использовать в ответ на одну из возможных стратегий природы , появляющуюся с вероятностью при условии

.

Известна также платежная матрица . Для снижения неопределенности относительно действительного состояния природы мы можем провести эксперимент, стоимость которого известна и равна . Пусть в результате проведения эксперимента состояние природы станет известно точно. Необходимо сделать вывод о целесообразности проведения эксперимента.

Наш средний выигрыш при использовании стратегии может быть определен как

. (9)

В качестве оптимальной стратегии может быть выбрана стратегия 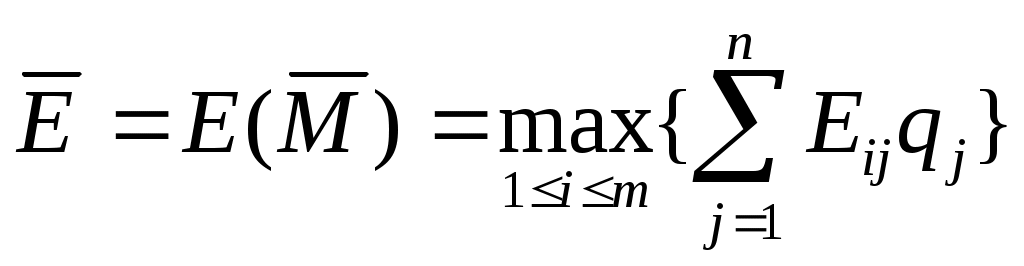, максимизирующая наш средний выигрыш

.

Предположим теперь, что в результате проведения эксперимента удалось точно установить стратегию природы . Очевидно, что в этом случае мы должны выбирать стратегию, обеспечивающую наш максимальный выигрыш

. (10)

Оценим теперь средний возможный выигрыш после проведения эксперимента



где ‑ стоимость проведения эксперимента. Отсюда появляется условие целесообразности проведения эксперимента



или

.

Преобразовывая неравенство, имеем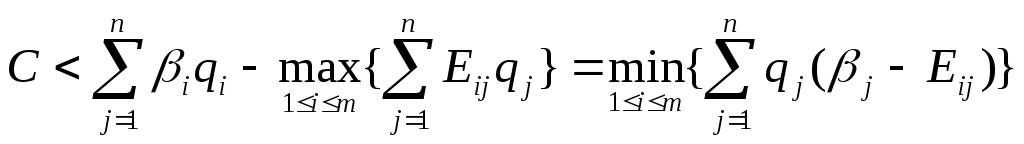

. (11)

Выражение в круглых скобках есть ничто иное как риск

.

Тогда правая часть неравенства есть минимальный средний риск, откуда вытекает условие целесообразности проведения эксперимента: затраты на эксперимент должны быть меньше минимального среднего риска, иначе от эксперимента следует воздержаться и в качестве оптимальной следует выбрать стратегию максимизирующую средний выигрыш или минимизирующую средний риск.

Рассмотрим случай, когда с помощью эксперимента не удается точно определить состояние природы, но возможно получить одно из несовместимых событий , связанных определенными вероятностями с состояниями (стратегиями) природы. Обозначим условную вероятность появления исхода эксперимента при условии стратегии природы символом . Поскольку образуют полную систему событий, справедливо

.

Будем считать, что все значения 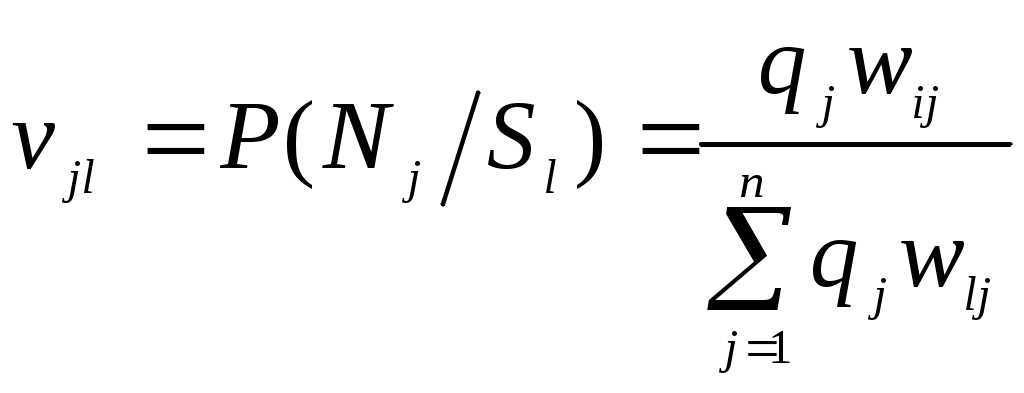известны, а также известна стоимость проведения эксперимента . Нас по прежнему будет интересовать вопрос: целесообразно ли проведение эксперимента и если да, то какую стратегию необходимо выбрать при том или ином исходе эксперимента. Предположим, что в результате эксперимента был получен результат . Определим апостериорные вероятности стратегий природы по теореме Байеса [6]

.

Далее для каждой стратегии рассчитаем величину условного среднего выигрыша при условии результата эксперимента

.

Очевидно, что оптимальной будет стратегия , обеспечивающая максимум условного среднего выигрыша при конкретном исходе эксперимента

.

Вероятность появления условного выигрыша совпадает с вероятностью появления события . Обозначим ее символом . Тогда

.

Величина выигрыша с использованием эксперимента

.

С другой стороны наш выигрыш без проведения эксперимента определяется выражением

.

Отсюда вытекает условие целесообразности проведения эксперимента



Если проведение эксперимента признано целесообразным, то необходимо разработать систему так называемых решающих правил, смысл которой сводится к следующему: какую стратегию необходимо выбрать, если эксперимент дал результат ?

Лабораторная работа №8. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой с экспериментами

Задание

Используйте придуманную вами задачу разработки управленческого решения. Задайтесь параметрами, которые могут быть в условиях неопределенности. Рассмотрите случай игры с природой с экспериментами и решите задачу.

Порядок выполнения работы

1. 
   Из общего числа параметров вашей задачи разработки управленческого решения выберите один, который будет рассматриваться в условиях неопределенности. Согласуйте с преподавателем выбранный вами параметр.
   
2. 
   На основе анализа ситуации в зависимости от возможных воздействий природы задайтесь возможными значениями случайного параметра , для которых будет делаться расчет. Каждое значение этого параметра будет определять одну из наших возможных стратегий
   
3. 
   Из числа значений случайного параметра задайтесь ( ) возможными значениями, которые определяют возможные стратегии природы и вероятности их появления , обеспечив выполнение условия
   

.

4. 
   Решая задачу с помощью надстройки Поиск решения, определите значение критериальной функции и соответствующие ему решения в предположении, что стратегия природы угадана, то есть мы предполагаем значение параметра , и в результате действий природы он принимает именно такое значение.
   
5. 
   Постройте платежную матрицу, заполните ее диагональ значениями и отдельно запишите соответствующие нашим стратегиям решения .
   
6. 
   Используя полученное решение для каждой строки подставляя соответствующее стратегии природы значение параметра в выражение для критериальной функции рассчитайте остальные элементы платежной матрицы .
   
7. 
   По формуле (1)) рассчитайте средний выигрыш при использовании каждой из наших возможных стратегий.
   
8. 
   Определите величину максимального среднего выигрыша и соответствующую ему стратегию .
   
9. 
   Предположите, что в результате эксперимента вам удалось точно узнать состояние природы. Тогда по формуле (1)) вычислите его величину для каждой вашей стратегии.
   
10. 
    Учитывая, что стратегии природы чередуются с некоторыми вероятностями , рассчитайте ваш выигрыш
    

.

11. 
    Задайтесь неким значением , определяющим стоимость такого эксперимента, и определите величину среднего выигрыша с учетом эксперимента .
    
12. 
    Определите результат вычисления неравенства и примите решение о целесообразности или нецелесообразности проведения эксперимента.
    
13. 
    Проведите исследование зависимости целесообразности проведения эксперимента от величины затрат .
    

Контрольные вопросы

1. 
   Чем игры с природой с экспериментами отличаются от обычных игр с природой?
   
2. 
   Что такое априорные данные?
   
3. 
   Когда целесообразно проведение эксперимента?
   
4. 
   Что такое единичный эксперимент?
   
5. 
   Что такое последовательный эксперимент?
   
6. 
   Как определить наш средний возможный выигрыш после проведения эксперимента?
   
7. 
   Как рассчитать максимальный средний выигрыш?
   
8. 
   Что представляет собой решение задачи?
   
9. 
   В чем отличие методики целесообразности определения эксперимента по критериям Вальда и Сэвиджа?
   
10. 
    Что такое апостериорные данные?
    

Отчет о работе

Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите обоснование выбора его значений. Представьте платежную матрицу и результаты ее обработки. Укажите предполагаемые затраты на эксперимент и полученные в соответствии с ними решения. Сформулируйте выводы, которые можно сделать по результатам выполненной работы.

Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б.