Системы поддержки принятия решения
 Скачать 3.85 Mb. Скачать 3.85 Mb.
|
2.4.Однокритериальная статическая задача разработки управленческого решения в условиях рискаВ литературе по экономике и менеджменту, в частности в учебниках по разработке управленческого решения, встречаются самые разнообразные определения понятия риска. Так, например, в [7] приводится следующая формулировка: риск – принятие решений в условиях, когда возможен неблагоприятный исход; вероятность отклонения величины фактического инвестиционного дохода от величины ожидаемого, неопределенность получения убытка при страховании. В [8] можно прочитать, что в самом широком смысле риск – это опасность возникновения ущерба. Объем этого понятия включает сферы деятельности по производству продукции, товаров, услуг, выполнению социально-экономических и научно-технических проектов, по товарно-денежным и финансовым операциям. Как отмечено там же, риск характеризуется на качественном и количественном уровнях в виде затрат (либо снижения доходов), а также может иметь абсолютное (физическое, материально-вещественное) или стоимостное выражение. Риск может быть рассчитан и в относительных показателях как отношение величины возможных потерь к сумме основных и оборотных средств предприятия либо к общим затратам ресурсов, ожидаемым доходам от намечаемых действий. В [9] указывается на тесную связь понятий риска и неопределенности, связывается неопределенность с разработкой управленческого решения, а риск с его реализацией, отмечается, что неопределенность – основная причина появления рисков. Все выше изложенные соображения являются, безусловно, правильными и широко используются в экономике и менеджменте. Следуя предложенным определениям, было бы логично объявить все не точно известные данные неопределенностями и ограничиться подсчетом возможных убытков в интегральном выражении. Тем не менее, аналитические науки, в частности исследование операций [3], разработали методы более точных расчетов результатов деятельности, связанной с различными неопределенностями. Эти методы базируются на более узком понимании терминов риск и неопределенность. Как указано в [3], принятие решения в условиях риска – это ситуация, когда действия по реализации принятого решения приводят к возможности появления одного из множества результатов, причем каждый результат имеет известную вероятность появления. Учитывая этот подход, будем использовать следующее определение: задача разработки управленческого решения в условиях риска предусматривает существование в определении критерия оптимальности и (или) в ограничениях стохастических факторов, то есть случайных величин с известными характеристиками. Иногда такие задачи называют стохастическими. В формулировке конкретной задачи случайный параметр может быть, например, один. Существуют задачи, когда таких параметров несколько, а в предельном случае все входящие в задачу параметры могут быть случайными величинами. Математически такая задача может быть записана как 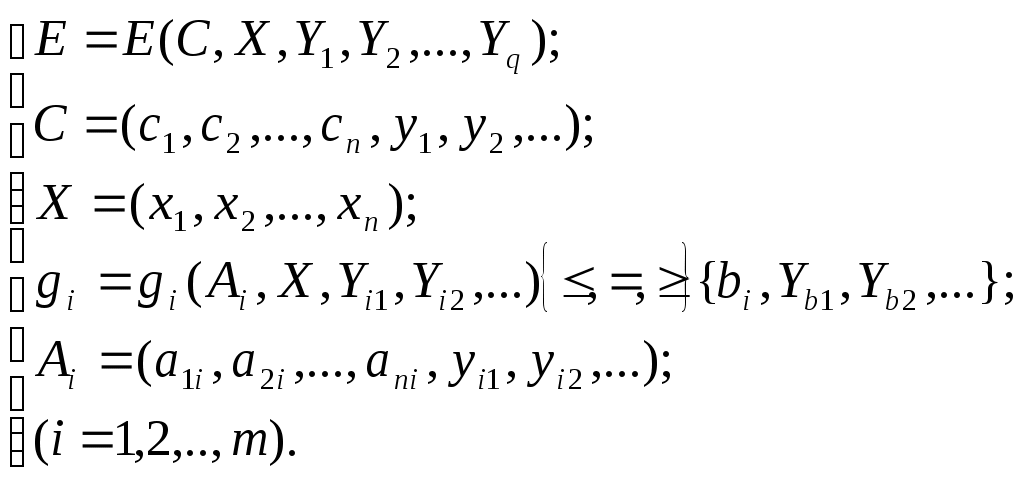 где символом Непосредственное решение задачи оптимизации со случайным значением параметра не имеет практического смысла. Действительно, найденное нами решение соответствует только одному из бесчисленного множества значений случайного параметра, которое может никогда не повториться. Поэтому полученное таким способом решение совсем не обязательно даст наилучшие результаты при повторяющихся экспериментах, так как сами значения критериальной функции начинают носить случайный характер. Для устранения этого несоответствия разработаны специальные методы решения подобных задач. Их классификация представлена на рис. 17. Методы решения задач в условиях риска. В соответствии с ней имеется две основные группы таких методов: сведение стохастической задачи к детерминированной и оптимизация в среднем. 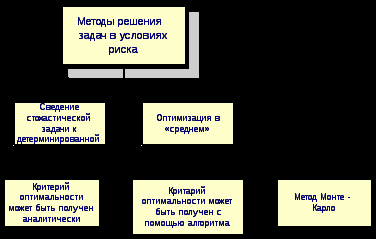 Рис. 17. Методы решения задач в условиях риска Метод сведения задачи в условиях риска к детерминированнойМетод сведения задачи в условиях риска к детерминированной может быть использован в том случае, когда в распоряжении исследователя имеется некоторая ограниченная выборка случайного процесса, в то время как точный вид закона распределения неизвестен. Обычно так бывает, когда на практике впервые сталкиваются с необходимостью учета случайного параметра, в то время как детальное исследование статистических свойств случайного процесса еще не произведено или его даже невозможно осуществить. В этом случае можно попытаться получить решение, которое использует только имеющиеся в нашем распоряжении данные. В основе метода лежит замена случайных параметров их неслучайными характеристиками, например, математическим ожиданием, максимальным и минимальным значением. Для отыскания решения на место случайного параметра подставляется значение его математического ожидания. Далее решается задача оптимизации тем же способом, каким она решалась в случае детерминированной задачи. Полученное решение рассматривается как основное. Дополнительно расчетом проверяются ситуации, когда случайный параметр имеет максимальное и минимальное значение. Как результат рассчитываются границы изменения критериальной функции при ранее полученном основном решении. Лабораторная работа №3. Решение однокритериальной статической задачи в условиях риска методом сведения стохастической задачи к детерминированнойЗаданиеИспользуйте придуманную вами задачу разработки управленческого решения. Задайтесь параметром, который может рассматриваться в условиях риска, и решите ее методом сведения стохастической задачи к детерминированной. Порядок выполнения работыИз общего числа параметров вашей задачи разработки управленческого решения выберите один, который будет рассматриваться в условиях риска (см. например, (1))) и согласуйте его с преподавателем. 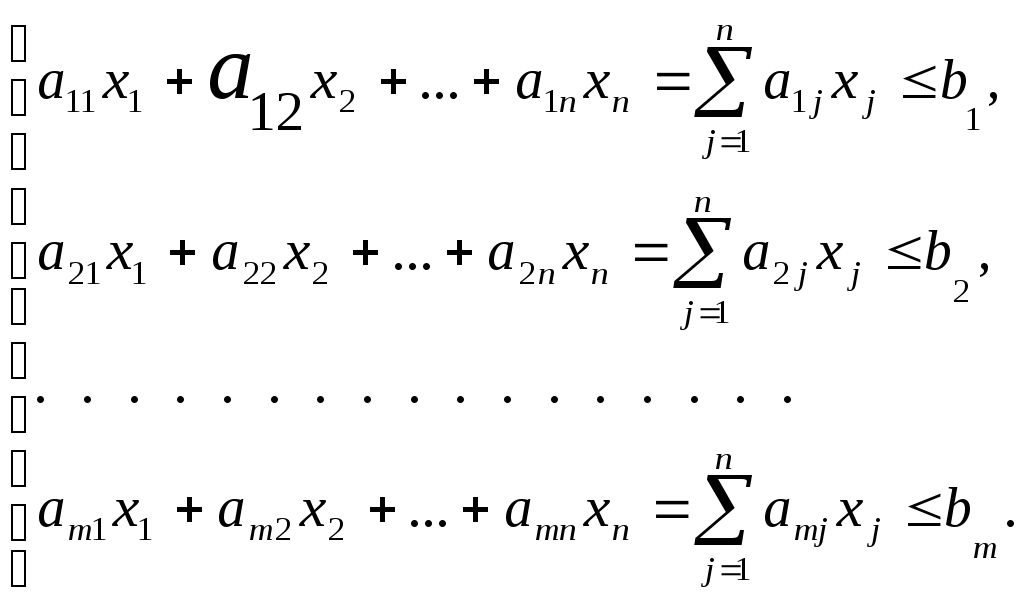 (7) (7)Получите выборку значений этого параметра и определите ее параметры (рис. 18). 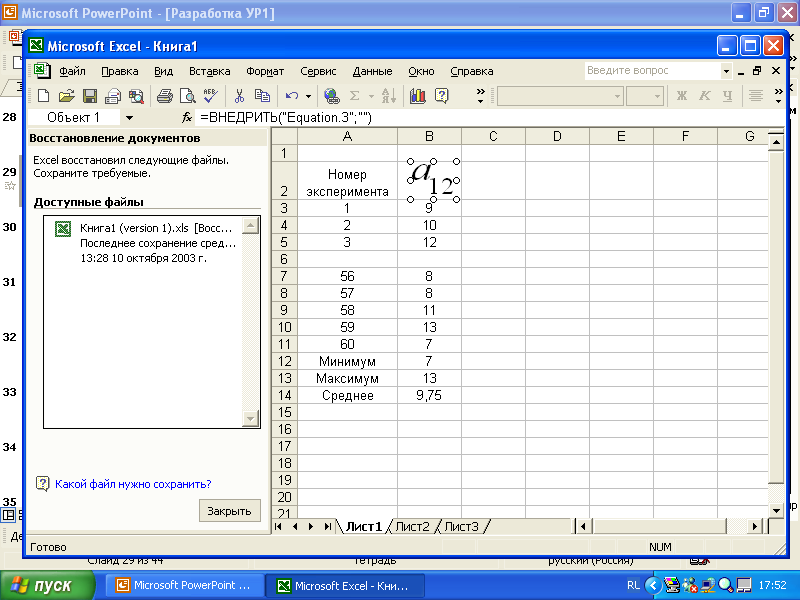 . .Рис. 18. Пример расчета параметров случайного процесса Подставьте на место параметра среднее значение и получите решение Используя решение Контрольные вопросыЧто такое риск? Чем задача в условиях риска отличается от детерминированной задачи? Какие детерминированные параметры случайного процесса вы знаете? Как определить детерминированные параметры случайного процесса? В чем заключается основная идея метода сведения задачи в условиях риска к детерминированной? Когда можно пользоваться методом сведения задачи в условиях риска к детерминированной? Какой смысл имеет решение, полученное при максимальном или минимальном значении случайного параметра? Почему нецелесообразно использовать решение, полученное при максимальном или минимальном значении случайного параметра? Почему в качестве оптимального используется решение, полученное при среднем значении случайного параметра? Как можно использовать значение критериальной функции, полученное при подстановке в оптимальное решение максимального или минимального параметра? Отчет о работеПодготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите используемый набор статистических данных и результаты его обработки. Приведите результаты решения задачи. Сформулируйте выводы, которые можно сделать по результатам выполненной работы. Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б. Методы оптимизации в среднемПо меткому замечанию одного из исследователей, методы теории принятия решения дают возможность получать плохие результаты в тех случаях, когда другими способами получить результаты оказывается просто невозможно. Во многом это утверждение можно отнести и к методу сведения задачи к детерминированной. Вполне естественно желание улучшить результаты решения за счет максимально возможного учета характеристик случайного процесса. Считается, что наиболее полная информация о нем содержится в функции распределения. Функция распределения случайной величины 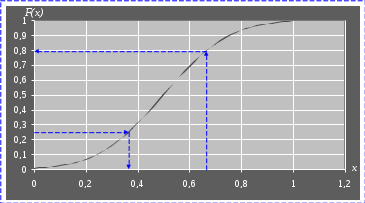 Рис. 19. Пример функции распределения случайной величины В зависимости от вида случайного процесса его функция распределения может описываться самыми разнообразными математическими выражениями. Случайная величина называется дискретной, если она может принимать только конечное или счетное множество значений. Для описания таких функций распределения пользуются, например, биноминальным, гипергеометрическим или пуассоновским распределениями [1]. Непрерывные случайные величины рассматриваются в совокупности с их плотностью распределения Задание функции распределения случайного параметра предусматривает задание его вида, т.е. собственно математического выражения, и значений параметров, входящих в это математическое выражение. Среди многих известных функций распределения упомянем распределение Гаусса или нормальное распределение, для которого Здесь Примечание. Определение вида закона распределения, т.е. математического выражения, описывающего функцию распределения случайной величины, представляет собой самостоятельную задачу исследования, которая выходит за пределы настоящей дисциплины. В то же время если это выражение известно (задано), то параметры закона распределения Методы оптимизации в среднем предусматривают замену ранее выбранного критерия оптимизации. Поскольку параметр принимает случайные значения, рассчитанная на его основе критериальная функция также становится случайной, в связи с чем задача ее максимизации становится бессмысленной. В то же время можно ставить и решать, например, задачу максимизации среднего значения критериальной функции. В литературе [5] этот вариант получил название М‑постановки задачи. Еще одним вариантом постановки задачи можно считать обеспечение некоторого значения целевой функции с заданной вероятностью (Р‑постановка). Для линейной задачи с где Аналитический метод решения задачи разработки управленческого решения предусматривает непосредственное вычисление выражения (1)). На практике, если дополнительно принимать во внимание ограничения, это оказывается весьма затруднительным. Поэтому при изучении настоящей дисциплины аналитический метод использоваться не будет. Алгоритмический метод решения задачи в условиях рискаМетод предусматривает существование алгоритма вычисления показателя эффективности, что собственно и реализовано, например, в виде надстройки Поиск решения. Предположим, что нам необходимо численно построить функцию распределения целевой функции. Зададимся набором вероятностей Лабораторная работа №4. Решение однокритериальной статической задачи в условиях риска алгоритмическим методомЗаданиеИспользуйте придуманную вами задачу разработки управленческого решения. Задайтесь параметром, который может рассматриваться в условиях риска, и решите ее алгоритмическим методом. Порядок выполнения работыЗадайтесь параметром, который может рассматриваться в условиях риска. Это может быть тот же самый параметр или какой-либо другой (тогда первый параметр рассматривается в условиях определенности). Согласуйте с преподавателем выбранный вами параметр. Задайтесь законом распределения случайного параметра. Получите выборку значений этого параметра и определите на ее основе параметры функции распределения. Задайтесь набором вероятностей Решая обратную задачу по заданным значениям вероятностей, определите величину параметра, значение которого не будет превышено с заданной вероятностью (например, при нормальном законе распределения, с помощью функции Excel НОРМОБР()). Подставляя значения параметра, решите оптимальную задачу (Поиск решения) и найдите значение критериальной функции и решение, соответствующее этому параметру. Постройте график функции распределения критериальной функции. Выберите оптимальное решение, соответствующее максимуму среднего значения критериальной функции (М‑постановка) или заданному значению вероятности (Р‑постановка). Контрольные вопросыПочему для решения задачи в условиях риска требуется замена критерия оптимальности? Как связаны между собой функция распределения и плотность распределения случайного процесса? Почему обычно выбирают нормальный закон распределения? Что такое обратная функция от функции распределения? В чем заключается основная идея аналитического метода? В чем заключается основная идея алгоритмического метода? Как осуществляется выбор оптимального решения при М-постановке? Как осуществляется выбор оптимального решения при Р-постановке? Какие соображения определяют выбор набора вероятностей Что представляет собой решение задачи в условиях риска? Отчет о работеПодготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите используемый набор статистических данных и результаты его обработки. Постройте график функции распределения целевой функции. Приведите результаты решения задачи. Сформулируйте выводы, которые можно сделать по результатам выполненной работы. Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б. Метод Монте-Карло при решении задачи в условиях рискаМетод предусматривает существование алгоритмической и программной модели решения задачи и замену реального случайного процесса его имитацией от датчика случайных чисел. Свое название метод Монте-Карло получил по имени казино, находящегося в княжестве Монако в одноименном городе, в котором исторически было сосредоточено большое число игровых заведений. Вероятно первые разработчики этого метода на основе анализа последовательностей случайных чисел, генерируемых колесом рулетки, пытались создать методику выбора очередного числа, на которое и должна была бы быть сделана ставка. Поскольку возможностей для непосредственных экспериментов в здании казино нет, было предложено определить закон распределения чисел для конкретного стола, а далее имитировать эту последовательность в лабораторных условиях с целью отыскания необходимого алгоритма. Заметим, что поскольку казино в Монако существуют до сих пор, этот эксперимент закончился неудачей. В соответствии с методом Монте-Карло на основании известной функции распределения случайного процесса генерируется выборка значений от датчика случайных чисел. В современной практике используется программная генерация таких чисел на основе стандартных и относительно несложных алгоритмов. Подобный подход позволяет, при необходимости, повторить генерацию выборки с заданным законом распределения или создать новую с тем же законом. Одним из недостатков программного метода является возникающая в некоторых случаях периодичность значений, борьба с которой ведется за счет настройки датчика. Тем не менее, говорить о том, что программным методом генерируется последовательность полностью случайных чисел, не приходится. Поэтому в литературе программные датчики называют обычно датчиками псевдослучайных чисел. Для решения задачи разработки управленческого решения методом Монте-Карло также необходимо знать функцию распределения случайного параметра. Если она известна, то исследователь может отказаться от реальных данных, получение которых сопряжено с известными трудностями, и заменить их выборками значений от программного датчика. Количество таких значений может существенно превышать объемы реальных выборок, но, в случае совпадения законов распределения реальных и сгенерированных данных, точность получаемых результатов существенно возрастает. При решении задачи в Excel для вызова датчика случайных чисел необходимо включить надстройку Анализ данных, в пункте Сервис главного меню выбрать пункт Анализ данных, а в открывшемся меню Инструменты анализа пункт Генерация случайных чисел. Основной задачей использования метода является построение функции распределения целевой функции с сохранением полученных для каждого значения решений. Далее на ее основе выбирается оптимальное решение, соответствующее вероятности Для каждого значения сгенерированного датчиком случайных чисел параметра решается оптимизационная задача и определяется значение критериальной функции и соответствующее ей решение. Далее строится гистограмма распределения критериальной функции, на основе которой принимается решение. Примечание. Гистограмма (эмпирическая плотность распределения) строится следующим способом. Проводится разбиение оси аргументов на конечное число граничащих друг с другом промежутков Подобный способ удобен при наличии программной реализации задачи математического программирования в виде, например, самостоятельной функции. При использовании для расчетов Excel для построения гистограммы достаточно в пункте Сервис главного меню выбрать пункт Анализ данных, а в открывшемся меню Инструменты анализа пункт Гистограмма. В открывшемся меню необходимо указать диапазон значений случайных чисел, сгенерированных от датчика, и в качестве параметров вывода Интегральный процент. При использовании надстройки Поиск решения каждый расчет требует некоторого количества ручных операций. Для уменьшения трудоемкости вычислений гистограмма распределения случайного параметра может быть построена до решения задачи оптимизации. В этом случае для расчета значений критериальной функции могут быть использованы средние значения карманов гистограммы, а соответствующие им значения критериальной функции встретятся в итоговом распределении столько раз, сколько они были в исходной гистограмме. Фактически задача в этом случае сводится к замене оцифровки оси абсцисс гистограммы распределения значениями критериальной функции при сохранении значений ординат. Лабораторная работа №5. Решение однокритериальной статической задачи в условиях риска методом Монте-КарлоЗаданиеИспользуйте придуманную вами задачу разработки управленческого решения. Задайтесь параметром, который может рассматриваться в условиях риска, и решите ее методом Монте-Карло. Порядок выполнения работыЗадайтесь параметром, который может рассматриваться в условиях риска. Это может быть тот же самый параметр или какой-либо другой. Согласуйте с преподавателем выбранный вами параметр. Задайтесь законом распределения случайного параметра. Получите выборку значений этого параметра и определите на ее основе параметры функции распределения. Запустите датчик псевдослучайных чисел и сгенерируйте выборку объемом не менее 10000 значений. Постройте гистограмму распределения случайных чисел от датчика. Рассчитайте средние значения карманов распределения Подставьте средние значение карманов гистограммы в качестве параметра и решите задачу оптимизации, определяя при этом решение и значение критериальной функции. Замените на построенной ранее гистограмме значения на оси абсцисс на значения критериальной функции и постройте график функции распределения целевой функции (интегральное представление). Выберите оптимальное решение, соответствующее максимуму среднего значения критериальной функции (М‑постановка) или заданному значению вероятности (Р‑постановка). Контрольные вопросыВ чем заключается основная идея метода Монте-Карло? Как воспользоваться датчиком случайных чисел? Почему программный датчик случайных чисел часто называют датчиком псевдослучайных чисел? В чем заключается основное достоинство метода Монте-Карло? Как принимается оптимальное решение при использовании метода Монте-Карло? Какие методы принятия решения на основе функции распределения критериальной функции вы знаете? Что такое гистограмма случайного процесса и чем она отличается от функции или плотности распределения? Как построить гистограмму распределения случайного процесса? Чем управляет ключ гистограммы Интегральный процент? Как определить параметры закона распределения при генерации случайных чисел? Отчет о работеПодготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите используемый набор статистических данных и результаты его обработки. Приведите график гистограммы распределения случайных чисел, сгенерированных датчиком. Постройте график функции распределения целевой функции. Приведите результаты решения задачи. Сформулируйте выводы, которые можно сделать по результатам выполненной работы. Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б. Задачи в условиях риска с несколькими стохастическими параметрамиМетодика решения задач в условиях риска с несколькими случайными параметрами базируется на расчете величины стохастической поправки, определяемой с учетом всех входящих в выражение случайных параметров. В простейшем случае случайные параметры считаются некоррелированными и распределенными по одинаковому закону распределения, например нормальному, с известными дисперсиями и математическими ожиданиями. Тогда детерминированный эквивалент вероятностного ограничения может быть записан в виде [6] где 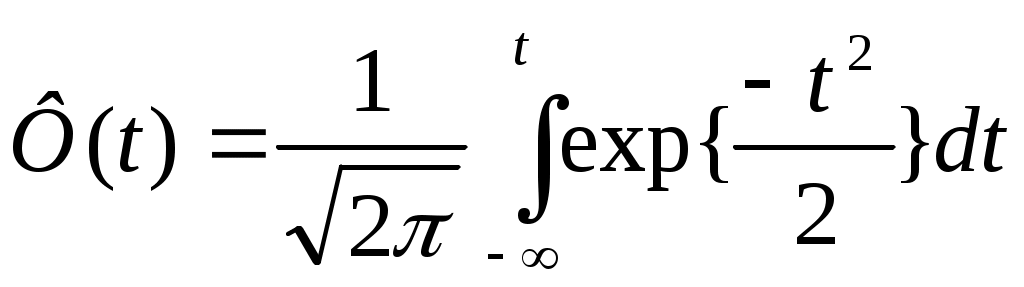 а |
