Системы поддержки принятия решения

• Название: Системы поддержки принятия решения
• Дата: 27.02.2023
• Размер: 3.85 Mb.
• Имя файла: Metodichka_SPPRLR240408.doc
• Тип: Методическое пособие; #957823
• страница: 10 из 28

2.5.Однокритериальная статическая задача в условиях неопределенности

Задача разработки управленческого решения в условиях неопределенности в отличие от задачи в условиях риска возникает в том случае, когда мы не располагаем никакой статистической информацией о параметрах случайных величин, не имеем их выборок и, как следствие, не можем составить или получить выражение для функции распределения, определить моменты и т.п. Поэтому рассчитать вероятность получения определенного значения показателя эффективности оказывается невозможным, хотя он и принимает случайные значения в каждом конкретном эксперименте при его многократном повторении.

Можно выделить два случая, характеризующих вероятность получения определенного значения критериальной функции. Во-первых, эти вероятности могут не иметь физического смысла, поскольку входящие в задачу неопределенные факторы имеют не стохастическую природу. К их числу относятся стратегические неопределенности, объясняющиеся участием в задаче нескольких разумных сторон, преследующих, в частности, противоположные цели. Неопределенность в задаче возникает потому, что нам неизвестны действия, которые будут предприняты сторонами (противником), и мы должны принимать решение в отсутствие полной информации. Кроме этого, в задаче могут возникать концептуальные неопределенности, связанные с принятием особо сложных решений и вызванные нечетким представлением о собственных целях и возможностях, целях и возможностях других сторон. Во-вторых, на решение задачи могут оказывать влияние стохастические неопределенности, возникающие из-за отсутствия информации о характере влияющих процессов, но не предусматривающие разумного вмешательства. В этом случае обычно говорят о воздействии природы на решение задачи, предполагая при этом отсутствие точек излома и разрыва и наличие инерционности в характеристиках мешающих факторов.

Наиболее сложным случаем для выработки управленческого решения является ситуация, когда у нас полностью отсутствует любая (в том числе и экспертная) информация о вероятностях возможных состояний природы. В этом случае решение приходится принимать исходя из анализа платежной матрицы или матрицы рисков. Согласно максиминному критерию Вальда выбирается стратегия, гарантирующая выигрыш не меньший, чем

.

Данный критерий ориентирует на наихудшие условия и рекомендует выбирать стратегию, для которой в самом тяжелом случае выигрыш максимален. Обычно критерий Вальда называют критерием крайнего пессимизма.

Критерий минимаксного риска Сэвиджа рекомендует в условиях неопределенности выбирать ту стратегию, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации. Сущность критерия Сэвиджа – любыми путями минимизировать риск. Критерий Сэвиджа также относится к критериям крайнего пессимизма, однако в этом случае в отличие от критерия Вальда худшим считается не минимальный выигрыш, а максимальная его потеря (максимальный риск)

.

Критерий пессимизма-оптимизма Гурвица рекомендует при выборе решения выбирать нечто среднее между крайним пессимизмом и оптимизмом



В этом выражении введенный Гурвицем некий коэффициент (мера пессимизма), выбираемый экспертным путем из интервала между 0 и 1. Очевидно, что при критерий Гурвица превращается в критерий Вальда.

Математически задача разработки управленческого решения в условиях неопределенности может быть записана в виде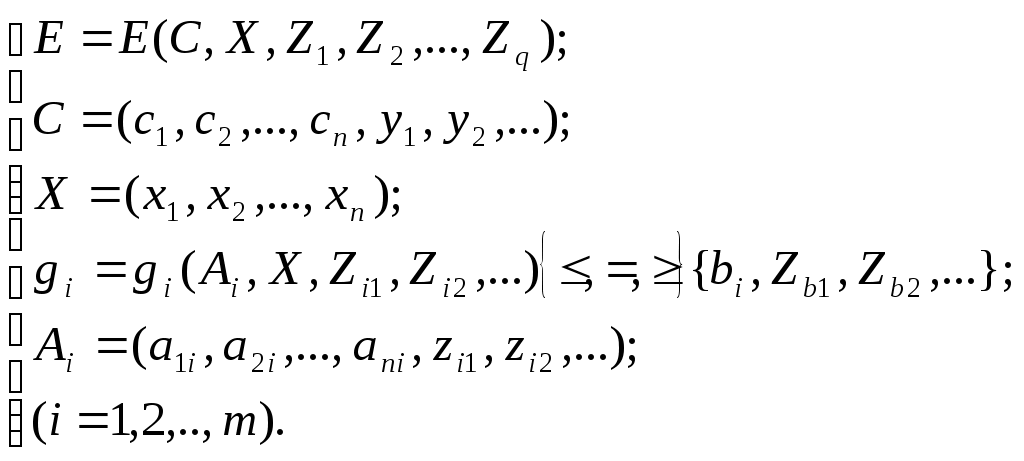



где - конкретная реализация неопределенного фактора. Неконтролируемые переменные принимают случайное значение и могут относиться либо к категории не стохастических (игры с противником), либо стохастических (игры с природой) случайных величин.

Основные методы решения задач в условиях неопределенности разработаны в математической теории игр [3, 10]. Предполагается, что правила игры известны всем ее участникам и обязательно выполняются. Каждый случай игры называется партией. Элементами партии являются ходы, которые могут быть личными (сознательное действие) и случайными. Каждый из игроков руководствуется совокупностью правил, однозначно определяющих выбор его ходов, называемую стратегией. Число таких стратегий может быть конечным или бесконечным. Результатом игры является выигрыш или проигрыш игроков. Например, если в игре участвуют только два игрока, преследующие прямо противоположные цели, то выигрыш одного игрока означает точно такой же проигрыш другого. Такая игра называется парной антагонистической игрой с нулевой суммой.