Системы поддержки принятия решения

• Название: Системы поддержки принятия решения
• Дата: 27.02.2023
• Размер: 3.85 Mb.
• Имя файла: Metodichka_SPPRLR240408.doc
• Тип: Методическое пособие; #957823
• страница: 13 из 28

2.7.Динамические задачи разработки управленческого решения

Общая постановка динамической задачи разработки управленческого решения

Задача разработки управленческого решения переходит в категорию динамических в том случае, когда входящие в ее состав параметры оказываются функциями времени. Следует отметить, что в некоторых задачах время может рассматриваться как ресурс. Его специфической особенностью является то обстоятельство, что расходом времени невозможно управлять. Вместе с тем учет времени как ресурса оказывается принципиальным для целого класса задач, в основе которых лежит, например, требование минимизации времени, затрачиваемого на выполнение работы.

В других задачах время может выступать в качестве дополнительного параметра, значение которого изменяется самопроизвольно по известному закону. Динамические задачи разработки управленческого решения могут рассматриваться как в предположении непрерывности времени как аргумента, так и в предположении, что значимые параметры задачи определяются только в некоторые фиксированные моменты времени. В первом случае говорят о непрерывных динамических задачах, а во втором о дискретных. Математически при переходе от непрерывной задачи к дискретной непрерывное время заменяется неким набором дискретных отсчетов , где - номер отсчета, а - шаг дискретизации, - номер отсчета. Обычно рассматривают эквидистантные задачи, для которых . Наконец, в некоторых случаях число рассматриваемых моментов времени может быть конечным.

Формально динамическая задача разработки управленческого решения может быть описана следующим выражением: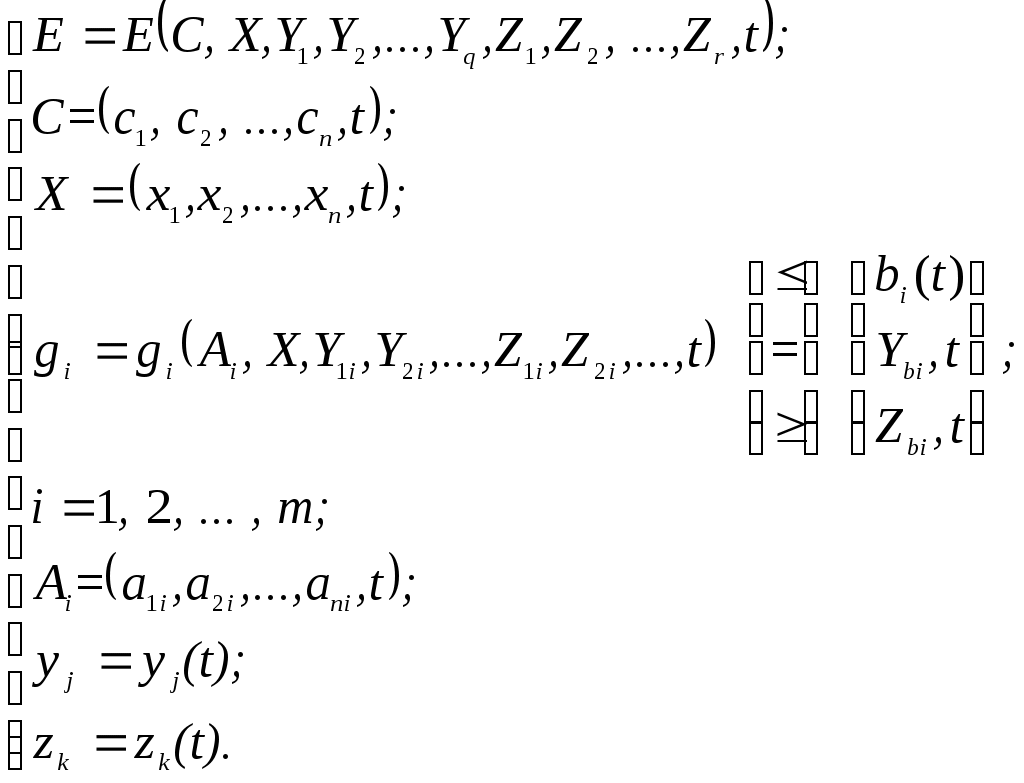



Дискретное представление исходных параметров заставляет вводить в рассмотрение не интегральные зависимости, а суммы. Формально такая замена проводится достаточно легко, однако в этой операции имеется ряд тонких моментов, которые необходимо принимать во внимание. К их числу следует в первую очередь отнести размер выборки . Если число сравнительно велико, а шаг дискретизации оказывается относительно небольшим, процедура дискретизации параметра не оказывает существенного влияния на результат решения (рис. 21 a).



Рис. 21 Дискретизация непрерывного процесса с маленьким а) и большим б) шагами

Ситуация существенно меняется в том случае, когда за время интервала дискретизации параметр успевает существенно измениться, а само число его отсчетов невелико (рис. 21 б). Если в первом случае можно говорить о приближенном дискретном представлении непрерывного параметра, то во втором речь идет о существенном искажении вида параметра, что приводит к серьезным изменениям в структуре решения и может дать существенно отличные результаты.

На настоящий момент отсутствует исчерпывающая классификация динамических задач разработки управленческого решения, поэтому далее представлена коллекция различных вариантов их постановки и методов решения.

Метод сетевого планирования

В основе методов сетевого планирования лежит так называемый сетевой граф, пример которого показан на рис. 22. Пример сетевого графа выполнения строительных работ. В кружках графа обычно отмечают различные события, например «Завершены монтажные работы». Стрелки графа означают собственно работу, которая может потребовать определенных ресурсов, в том числе и времени. Важной особенностью сетевого графа является возможность определения полного времени, которое требуется на выполнение работы. Оно определяется так называемым критическим путем, который представляет собой последовательность событий, достижение которых требует максимально большого времени. Очевидно, что если бы граф не имел разветвлений, то полное время выполнения работ совпадало бы с суммой времен, затраченных на каждую работу. Однако, в случае ветвлений, некоторые из работ параллельных ветвей могут быть завершены раньше. Тогда полное время выполнения параллельных работ определяется временем выполнения самой длинной работы. Она и оказывается на критическом пути.

Применительно к сетевому графику может быть поставлена задача оптимизации использования материальных, трудовых и финансовых ресурсов. Например, если имеется несколько параллельных ветвей графа, то работа, лежащая на критическом пути, обязательно должна быть обеспечена всеми необходимыми ресурсами. В то же время остальные работы могут, при необходимости, начаты с некоторой задержкой. Эта задержка может быть запланирована и использована для того, чтобы один и тот же ресурс первоначально использовался для выполнения одной работы, а потом другой. Время окончания любой работы должно быть согласовано с временем окончания работы, лежащей на критическом пути, поскольку иначе задержанная с началом работа сама окажется на критическом пути.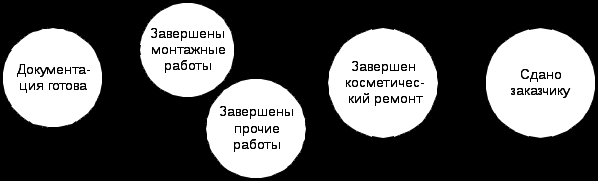



Рис. 22. Пример сетевого графа выполнения строительных работ

Сетевой график может рассматриваться как в условиях определенности, так и в условиях риска и неопределенности. В случае риска можно говорить и среднем времени выполнения работы и рассчитывать его теми же методами, которые использовались при решении статических задач. Аналогично в случае неопределенности можно рассматривать оптимальные стратегии.

Сетевые графики широко используются в современной методологии управления различными видами деятельности, имеющими четко обозначенное начало и конец, и получившими название «Управление проектами». Проект – комплекс взаимосвязанных мероприятий, предназначенных для достижения в течение заданного времени и при установленном бюджете поставленных задач с четко определенными целями.

Для поддержки проекта существуют специальные программные средства, позволяющие автоматизировать многие операции, связанные с разработкой, оптимизацией и реализацией проекта. На рис. 23 показан пример выдачи программой пакета Microsoft Project последовательности работ проекта в виде так называемой диаграммы Ганта. Удобство такой диаграммы заключается в том, что система сразу выделяет цветом работы, находящиеся на критическом пути, а также дополнительно выдает информацию о сроках (датах) каждой работы. Кроме этого, система может строить и обычный сетевой график (рис. 22. Пример сетевого графа выполнения строительных работ), отображать загрузку и расход ресурсов, контролировать ход выполнения проекта, в том числе и расход его сметы и многое другое.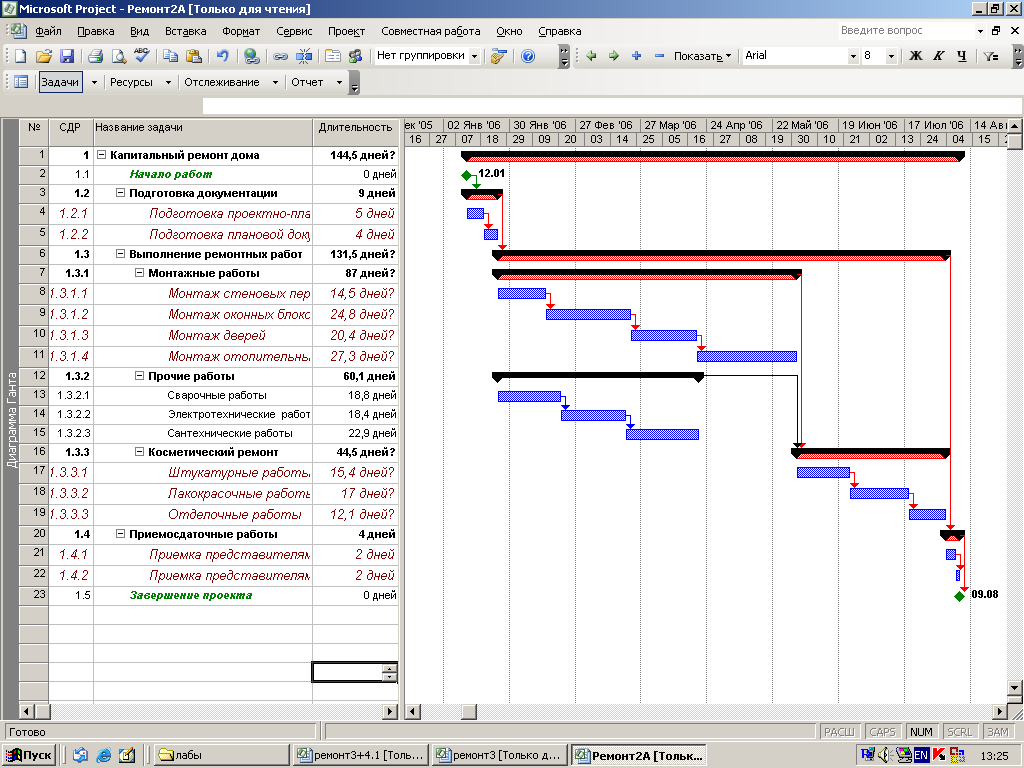



Рис. 23. Диаграмма Ганта.

Методы теории массового обслуживания

Система массового обслуживания – это модель некоторой реальной системы, в которой имеется случайный поток требований на обслуживание, которое ведется в системе с некоторыми определенными правилами. Теория массового обслуживания имеет своей целью разработку методов и моделей оценивания эффективности процессов массового обслуживания и качества реализующих их систем, а также моделей и методов организации данных процессов и систем, обеспечивающих требуемую их эффективность и качество [10]. На рис. 25 в качестве примера приведен один из простейших вариантов таких систем.

Задачи разработки управленческого решения, решаемые методами теории массового обслуживания, относятся к категории задач в условиях риска, а основным методом решения подобных задач можно считать метод Монте-Карло. Оптимизация принимаемых решений на основе использования теории массового обслуживания может вестись, в частности, за счет выбора количества устройств обработки требований на обслуживание.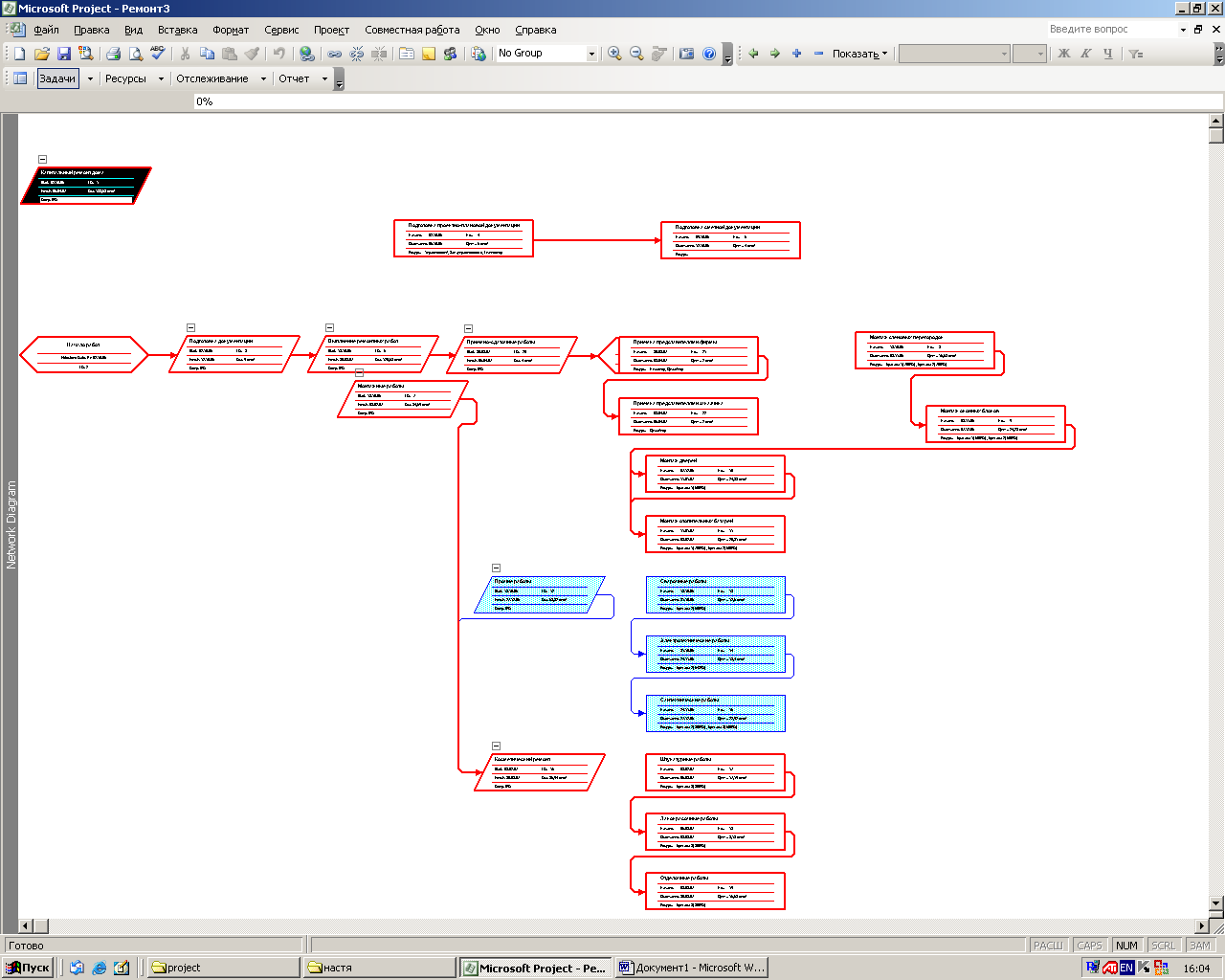



Рис. 24. Сетевой график, выдаваемый системой управления проектами



Рис. 25. Пример одноканальной системы массового обслуживания

Метод динамического программирования

Динамическим программированием называется метод оптимизации, в котором процесс принятия решения может быть разбит на шаги [11]. Каждый шаг переводит объект управления из состояния в состояние посредством управления . Если общее количество шагов равно , то можно говорить о последовательности состояний системы, которую она принимает в результате воздействия различных управлений Целевая функция системы зависит от начального состояния и управления

.

Предполагается, что состояние системы в конце -того шага зависит только от предшествующего состояния и управления на -том шаге . Тогда уравнение состояния системы имеет вид



Если считать целевую функцию аддитивной от показателя эффективности каждого шага, то на шаге и целевая функция имеет вид



Решением задачи динамического программирования является определение такого управления , которое переводит систему из состояния в состояние при наибольшем (наименьшем) значении .

Для решения задачи динамического программирования был сформулирован так называемый принцип оптимальности. Его смысл которого сводится к следующему: каково бы ни было состояние системы в результате выполнения какого-либо числа шагов, управление на ближайшем шаге нужно выбирать так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к максимальному выигрышу на всех оставшихся шагах включая данный.

Рассмотрим последний шаг . Состояние системы к началу шага , управление, а - целевая функция. Согласно принципу оптимальности управление нужно выбирать так, чтобы для любого состояния получался условный максимум целевой функции



Решение , при котором достигается называется условным оптимальным управлением на шаге . Условный максимум целевой функции отыскивается для всех возможных состояний системы на последнем шаге. Далее рассматривается совместно последний и предпоследний шаг. Целевая функция в этом случае имеет вид



Отыскивается условное оптимальное управление на двух последних шагах для всех возможных состояний системы на предпоследнем шаге



Состояние системы при известном управлении определяется как , в связи с чем целевая функция зависит только от состояния на предыдущем шаге и текущего управления. Далее рассматривается три, четыре и т.д. последних шага. В общем случае для шага получается уравнение Белмана, впервые разработавшего метод динамического программирования.



В результате условной оптимизации могут быть получены последовательности значений критериальной функции и условных управлений





Решение задачи динамического программирования получается в результате подстановки конкретного значения в выражение для решения на первом шаге и . Далее определяется состояние первого шага



и так далее для всех шагов. Оптимальное решение задачи получается при последовательном расчете оптимальных решений и и новых состояний .

При практической реализации метода динамического программирования на ЭВМ возникает ряд трудностей, связанных, в частности, со способами описания состояния объекта управления. Как правило, рассматривается конечное число состояний объекта управления на каждом шаге. Тем не менее, наибольший интерес представляет случай отыскания оптимального состояния объекта из бесконечного числа возможных состояний, например, методом математического программирования. В доступной литературе такие материалы отсутствуют, кроме того, не имеется сведений о программной реализации метода динамического программирования, хотя потребность в решении таких задач в достаточно велика. Из сказанного следует, что доведение методов динамического программирования до практического использования представляет собой актуальную и важную задачу исследования.

Задача управления запасами

Задача управления запасами впервые была описана и решена в 1915 году Фордом Хариссом. В ее основе лежит проблема, связанная с рассогласованием режимов работы поставщика и потребителя. Наличие склада позволяет обеспечить независимость работы потребителя от условий поставки материальных ресурсов. Задача управления запасами имеет цель отыскания решения, минимизирующего общие затраты на приобретение и хранение запасов. Предполагается, что общая сумма затрат на хранение запасов складывается из двух основных составляющих: затраты на пополнение запасов (издержки поставок) и затраты на собственно хранение (издержки по содержанию запаса).

Издержки поставок включают стоимость получаемого товара, расходы по доставке и контролю, оформлению документации, предварительные расходы на поиск поставщика и оформление с ним договора. Часть издержек поставок зависит от размеров поставляемой партии материалов, а часть зависит только от самого факта поставки и пропорциональна числу партий. Логично предположить, что издержки поставок уменьшаются с ростом размера заказа. Тогда из соображений их уменьшения целесообразно делать заказ как можно реже максимально большим объемом.

Издержки по содержанию запаса включают расходы по складскому помещению (электроэнергия, тепло), на оплату труда персонала, страховку, потери материала, на амортизацию капиталовложений в оборудование склада, потери от связывания средств в незавершенном производстве. Сюда же могут быть отнесены потери от старения товара, порчи и хищений. Естественно предположить, что издержки по содержанию запаса растут по мере увеличения объема запаса, а из соображений их уменьшения было бы хорошо иметь минимальный объем запасов и даже, если возможно, вообще отказаться от складского хозяйства.

На рис. 26 представлен график зависимости величины запаса от времени. При управлении запасами необходимо выбирать момент заказа и объем партии. Сами запасы могут расходоваться также партиями, (например, суточная норма). Это обстоятельство отмечено на графике ступеньками. Отсутствие запаса на складе может привести к остановке производства и, как следствие, штрафным санкциям.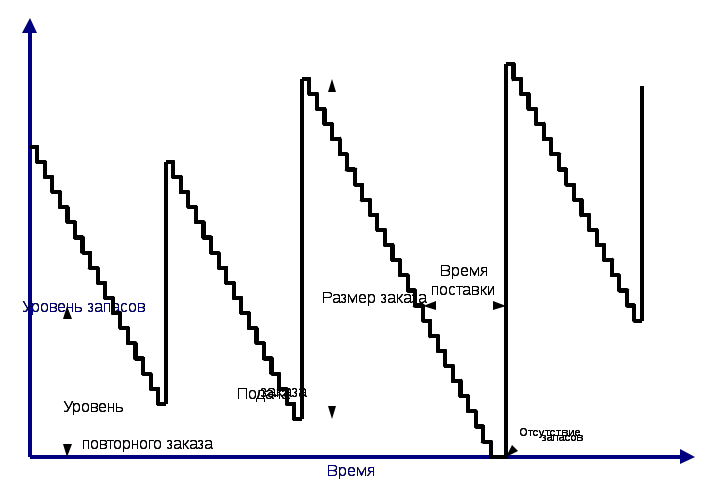



Рис. 26. Зависимость запаса от времени

Пусть штрафные санкции отсутствуют. Будем считать, что издержки поставок зависят только от числа поставок, а заказ выполняется одинаковыми партиями , следующими с интервалом с издержками на поставку каждой партии . Тогда за время будет поставлено партий товара размером , а общие издержки составят .

Кроме этого будем считать, что издержки от хранения пропорциональны размеру хранимой партии (рис. 27). Предположим, что заказ выполняется мгновенно, а партия расходуется равномерно и на момент заказа складской запас отсутствует. Тогда выражение полных издержек (рис. 27) будет иметь вид



Общие затраты на хранение имеют выраженный минимум. Поэтому возникает оптимизационная задача. Дифференцируя по , имеем



откуда размер оптимальной партии



Последнее выражение в литературе получило название формулы Уилсона или формулы наиболее экономичного объема партии.

Задача управления запасами становится многономенклатурной, если в рассмотрение принимается несколько видов запасов с разными условиями поставки и расходования. В этом случае можно минимизировать как затраты на поставку и хранение каждого вида запасов, так и всех запасов совместно.



Рис. 27. Зависимость затрат на запасы

Методы вариационного исчисления и теории оптимального управления

Вариационное исчисление – математическая дисциплина, посвященная отысканию экстремальных (наибольших или наименьших) значений функционалов [1]. В свою очередь под функционалом понимается числовая (действительная или комплексная) функция, определенная на некотором множестве функций. Вариационное исчисление является естественным развитием той главы математического анализа, которая посвящена задаче отыскания экстремумов функций. В основе постановки задач классического вариационного исчисления лежат задачи управления физическими процессами. Во всех вариантах таких задач речь идет о способе задания наилучшего в том или другом смысле управления, обеспечивающего минимизацию или максимизацию некой цели управления.

В одной из возможных постановок [6] предметом вариационного исчисления является отыскание неизвестных функций 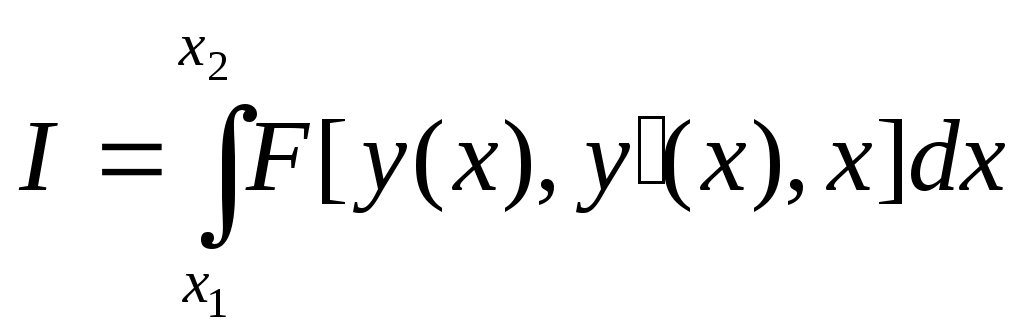или 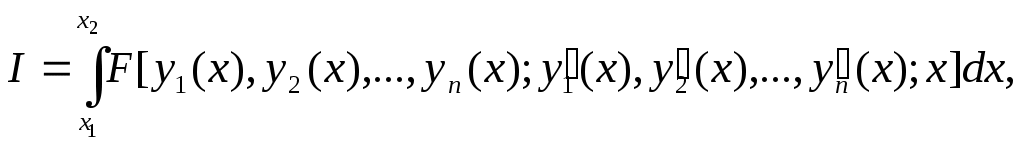, реализующих максимум или минимум определенных интегралов вида



или



где ‑ функция, описывающая взаимосвязь поведения объекта в зависимости от управления. На функцию накладывается ряд требований, в частности, требования непрерывности производных на интервале определения, что всегда обеспечивается в задачах с физическими процессами и не всегда в задачах экономики и менеджмента. В большинстве приложений функции или выбираются не среди множества всех возможных функций от , а среди множества функций определенного класса. Такое допущение оправдано в связи с тем, что возможности управления процессом очень часто ограничивают класс возможных функций неким заранее заданным.

Развитие идей вариационного исчисления привело к определенной модернизации постановки исходной задачи в виде учета ограничений функции и созданию теории оптимального управления. Методы решения подобных задач опираются на реализацию так называемого принципа максимума Понтрягина [1]. Практическая реализация методов вариационного исчисления и теории оптимального управления позволяет решать динамические задачи разработки управленческого решения.

Метод сведения дискретной динамической задачи к статической

Одним из возможных методов разработки управленческого решения для динамических задач является метод, основанный на представлении динамической задачи в виде набора самостоятельно существующих статических задач. Пусть рассматривается дискретных моментов времени. Для каждого из них можно сформулировать самостоятельную задачу разработки управленческого решения (например, однокритериальную статическую в условиях определенности) ¹



где - текущий дискретный момент времени, .

Рассмотрим совместную однокритериальную статическую задачу в условиях определенности, решение которой 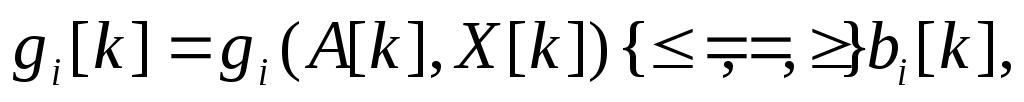представляет собой набор из самостоятельных решений для текущего момента времени . Будем считать, что критериальная функция новой совместной задачи определяется как сумма критериальных функций для каждого момента времени, а ограничения для каждого момента времени добавляются к общему списку ограничений задачи. Тогда условие новой задачи можно записать как





а общее количество уравнений ограничений увеличилось в раз. Таким образом, решение динамической задачи сводится к решению статической задачи разработки управленческого решения и может осуществляться рассмотренными ранее методами.

Реализация метода в общем случае приводит к существенному росту трудоемкости вычислений. Отметим, что если количество переменных при использовании метода всегда возрастает в раз, то число уравнений ограничений может быть значительно сокращено за счет конкретного рассмотрения динамических параметров. Так, если к категории динамических относятся один или несколько параметров , то рассмотрение каждого из них во времени увеличивает количество ограничений в раз. Для статических нет необходимости увеличивать количество уравнений, поскольку в этом случае они имеют смысл величины имеющегося ресурса на весь интервал планирования. Наконец, зависимость от времени неконтролируемых факторов и вообще может быть легко учтена при записи выражения целевой функции или ограничений особенно в численной форме.

Практическая реализация метода сведения динамических задач к статическим может быть осуществлена с использованием современных программных средств, реализующих, например, метод линейного программирования. При выборе используемой программы следует обращать внимание на ограничения программы по максимальному числу переменных и ограничений. Таким образом, метод сведения динамических задач к статическим может быть использован для решения динамических задач разработки управленческого решения.

Лабораторная работа №10. Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической

Задание

Используйте придуманную вами задачу разработки управленческого решения. Переведите ее в категорию динамических дискретных задач и найдите решение, обеспечивающее экстремум критериальной функции задачи, записанной как сумма ее значений для каждого момента времени

Порядок выполнения работы

1. 
   Возьмите в качестве основы решенную вами в процессе выполнения лабораторной работы №2 однокритериальную статическую задачу в условиях определенности.
   
2. 
   Определите параметр задачи, который будет рассматриваться как зависящий от времени. Согласуйте с преподавателем выбранный вами параметр.
   
3. 
   Задайтесь количеством интервалов времени , применительно к которым будет решаться задача.
   
4. 
   Увеличьте общее количество переменных задачи в раз. Например, при для задачи, изображенной на рис. 9, общее количество переменных станет равным 12. Для определенности в обозначения решения введите указание момента времени. Например, обозначение означает третий элемент вектора управления, рассматриваемый в момент времени .
   
5. 
   Задайте значения весовых коэффициентов целевой функции для . Например, просто скопируйте в соответствующие ячейки рабочего листа значения , если вы считаете, что они не зависят от времени.
   
6. 
   Вставьте, если это необходимо, дополнительные строки ограничений для , дополнив значениям параметры при . Повторите эти действия для всех остальных возможных значений .
   
7. 
   Запрограммируйте выражения, определяющие расход соответствующего ресурса с учетом увеличения общего числа неизвестных задачи.
   
8. 
   В соответствующих строках задайте величины ограничений для каждого момента времени .
   
9. 
   Запрограммируйте общее выражение для целевой функции как сумму произведений значений на и назначьте эту ячейку в качестве целевой в надстройке Поиск решения (рис. 7).
   
10. 
    В поле Изменяя значения укажите все значения .
    
11. 
    В поле Ограничения введите величины израсходованных ресурсов, знаки неравенств и наличие ресурса..
    
12. 
    Решите задачу поиска оптимального решения и получите оптимальное решение .
    
13. 
    Проведите исследование зависимости решения от характера изменения динамического параметра.
    

Контрольные вопросы

1. 
   Когда задача становится динамической?
   
2. 
   В чем заключается отличие дискретных задач от непрерывных?
   
3. 
   Как шаг дискретизации влияет на качество преобразования непрерывного сигнала к дискретному?
   
4. 
   Как ставятся задачи оптимизации в управлении проектами?
   
5. 
   Как ставятся задачи оптимизации в теории массового обслуживания?
   
6. 
   В чем основная идея метода динамического программирования?
   
7. 
   Как ставятся задачи оптимизации при управлении запасами?
   
8. 
   Для каких целей можно использовать преобразования Фурье?
   
9. 
   Чем постановка задачи теории оптимального управления отличается от постановки задачи вариационного исчисления?
   
10. 
    В чем заключается основная идея метода сведения дискретной динамической задачи к статической?
    

Отчет о работе

Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите динамические параметры, взятые в рассмотрение, и обоснуйте его выбор. Представьте таблицу результатов решения задачи. Сформулируйте выводы, которые можно сделать по результатам выполненной работы.

Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б.