Разное. диплом многозначные (pdf.io). Содерж
 Скачать 1.23 Mb.
|
|
311 4?   217? 1244 1461?а) 6 б) 7 в) 5 г) 8 51 2. Замени выражение в виде произведения двух чисел и найди его произведение. (500+70+3)·(80+4)= (2000+400+50+2)·(30+5)= 3. Найди неизвестное делимое. … : 12 = 753 … : 35 = 48 (ост.10) … : 66 = 123 (ост.43) 4. Что общего у значений произведений чисел: 17·8 18·12 26·36 а) имеют 6 в разряде единиц б) имеют 3 в разряде десяток в) имеют 8 в разряде сотен 5. Восстанови пропущенные цифры, обозначенные знаком *.  867*6 **** 3468 ***** После проверки данной работы были получены следующие результаты: Оценки     Оценка "5" Оценка "4" Оценка "3" Оценка "2"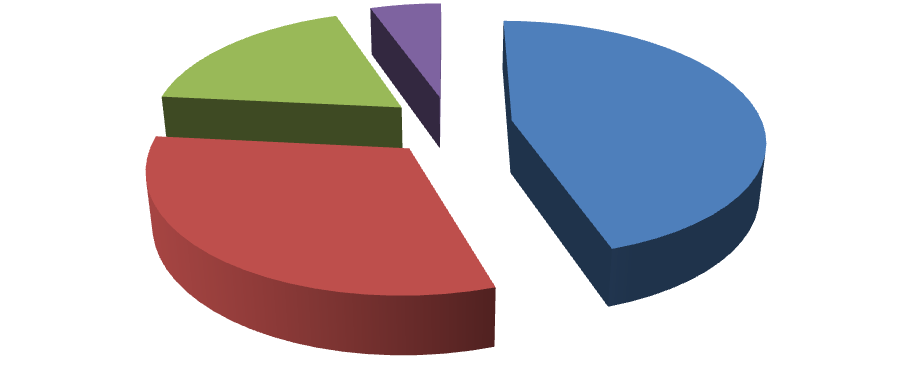 5% 18%45% 32% 52 В 4 «Б» экспериментальном классе 45% учеников от общего числа учащихся 4 «Б» класса после проведенного эксперимента имели высокий уровень сформированности умений умножать многозначные числа (на 23% больше по сравнению с констатирующим этапом эксперимента), у 32% учащихся был выявлен уровень выше среднего (на 10% больше по сравнению с констатирующим этапом эксперимента), 18% учащихся 4 «Б» класса имели средний уровень сформированности умений умножать многозначные числа (на 4% меньше по сравнению с констатирующим этапом эксперимента) и лишь 5% учеников от общего числа учащихся 4 «Б» класса имели уровень ниже среднего, что на 21% меньше по сравнению с констатирующим этапом эксперимента. Проанализировав результаты и проведя сравнение выполненных работ на констатирующем и контрольном этапах, мы пришли к выводу, что оценки учащихся улучшились, стало меньше ошибок на знание таблицы умножения, дети лучше усвоили разрядный состав числа и свойства умножения. Но допускаются ошибки по невнимательности, забывают о переходе через разряд. Исходя из вышесказанного, можно сказать, что проведенная работа была достаточно эффективна, так как полученные результаты улучшились, но необходимо целенаправленно систематически продолжать совершенствовать вычислительные навыки младших школьников умножения многозначных чисел. 53 |