психология. ГОС по педагогике и психологии. Сократ (469399 до н э.), Платон
 Скачать 1.87 Mb. Скачать 1.87 Mb.
|
|
2. Понятие о способностях и их природе. Виды способностей. Условия развития способностей. Способности — это индивидуально-психологические особенности человека, отвечающие требованиям данной деятельности и являющиеся условием успешного ее выполнения. К индивидуальным способностям относятся, например, музыкальный слух и чувство ритма, воображение, быстрота двигательных реакций. Человек не рождается способным к той или иной деятельности, его способности формируются, складываются, развиваются в соответствующей деятельности, в течение его жизни, под влиянием обучения и воспитания. Иными словами, способности — прижизненное, а не врожденное образование. Виды способностей Способности человека еще не гарантируют успешного выполнения им сложной деятельности. Различают способности разного уровня — учебные и творческие. -Учебные способности связаны с усвоением уже известных способов выполнения деятельности, приобретением знаний, умений и навыков. -Творческие способности связаны с созданием чего то нового, с нахождением новых способов выполнения деятельности. -Умственные способности — это способности, которые необходимы для выполнения не какой-то одной, а многих видов деятельности; эти способности отвечают требованиям, которые предъявляют не одна, а целый ряд, например, такие качества ума, как умственная активность, критичность, систематичность, сосредоточенное внимание и т.д. -Специальные способности — это способности, которые необходимы для успешного выполнения какой- нибудь одной определенной деятельности — музыкальной, художественно-изобразительной, математической, литературной. -Музыкальные способности составляют единство таких способностей, в эмоциональном восприятии и легком узнавании мелодий, способность к слуховому представлению, музыкальной памяти, музыкально-ритмическое чувство — способность чувствовать ритм и воспроизводить его. 3. Внетабличное деление. Самое первое, с чего нужно начать, это подобрать круглое число, которое делится на 7. Самое близкое круглое число — это 70. Отлично, половина дела уже сделана! Второй шаг — из делимого (а это то число, которое мы делим) надо отнять найденное нами круглое число. Если мы от 91 отнимем 70, то получим 21. Прекрасно! Мы сделали большую часть стратегии. Осталось каждое из найденных чисел: 70и 21 разделить на 7, а потом сложить итоговые значения. 70:7=10 21:7=3 10+3=13 Ответ: 91:7=13 99 : 9 = ? 2 .Рассуждай так: В числе 99 – 9 десятков и 9 единиц; делю 9 десятков на 9, получаю 1 десяток, или это число 10; далее делю 9 единиц на 9 и получаю число 1. Теперь к 10 прибавляю 1 и получаю 11. Тогда, 99 : 9 = 11 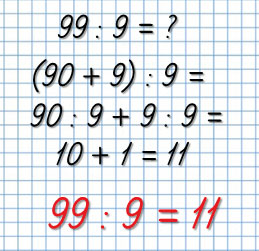 84 : 4 = ? Рассуждай так: В числе 84 – 8 десятков и 4 единицы; делю 8 десятков на 4, получаю 2 десятка, или это число 20; далее делю 4 единицы на 4 и получаю число 1. Теперь к 20 прибавляю 1 и получаю 21. Тогда, 84 : 4 = 11 Билет №12 Формы организации учебного процесса в школе (экскурсия, факультативные занятия, домашняя работа, предметные кружки). Наряду с уроком в общеобразовательных учреждениях используются и другие формы учебной работы. Основное распространение получили такие формы, как экскурсия, домашняя работа, факультативные занятия, мероприятия внеклассной работы (предметные кружки, студии, олимпиады, конкурсы и пр.). Экскурсия. Одной из наиболее интересных для учащихся форм обучения является экскурсия. Экскурсия – форма организации учебной работы, при которой учащиеся выходят на место расположения изучаемых объектов (природы, исторических памятников, производства) для непосредственного ознакомления с ними. Она объединяет учебный процесс в школе с реальной жизнью и помогает учащимся через непосредственные наблюдения познакомиться с предметами и явлениями в их естественном окружении. В зависимости от дидактической цели выделяют: вводные экскурсии, проводимые перед непосредственным изучением нового материала; текущие и итоговые, которые проводятся для контроля и лучшего закрепления изученного материала. По предметному содержанию экскурсии можно разделить на естественнонаучные, историко-литературные, краеведческие, производственные и др. В школьной практике обучения экскурсии проводятся не часто, и поэтому лучше, чтобы одна экскурсия содержала в себе информацию сразу по нескольким учебным предметам, чтобы учащиеся могли составить полную картину реальной действительности. Такие экскурсии называются комплексными. Например, можно проводить экскурсию в лес, изучая виды растущих там деревьев и одновременно устно решая математические задачи, главными героями которых являются изучаемые деревья. Гармонично включаются в такие экскурсии рассказы учителя о своем крае и его истории, об экологических проблемах данной территории. Экскурсии обычно планируются на весь учебный год и проводятся в специально отведенные дни, свободные от других занятий. В каждой школе составляется план экскурсий, в него включаются как учебные, так и внеучебные экскурсии, проводимые по плану классного руководителя. Чаще всего все экскурсии связаны с изучением материала, заложенного в программе по предметам. При проведении экскурсии выделяют три этапа: а) предварительную подготовку к экскурсии на уроках; б) выезд учащихся к изучаемому объекту и проведение запланированного объема учебной работы по теме занятия (сбор природного материала, рисунки, чертежи и т.д.); в) работа с собранным материалом и подведение итогов экскурсии. При подготовке к экскурсии учитель проводит тщательное изучение объекта экскурсии, места ее проведения, определяет ее цели и задачи. После этого учитель выбирает содержание материала и виды деятельности, которые учащиеся будут осваивать при подготовке, во время и после окончания экскурсии. Учитель выбирает методики показа и рассмотрения объекта экскурсии, способы вовлечения учащихся в активное восприятие, привлечение к показу и рассказу специалистов и пр. В подготовку входит и обучение учащихся способам сбора материала: приемам ведения записей, зарисовок, основам фотографирования, звукозаписи рассказов экскурсовода и т.д. Перед выходом на экскурсию проводится вступительная беседа, уточняются задания, определяются формы, порядок и сроки их выполнения, время, отводимое на экскурсию и сбор материала. До экскурсии учитель распределяет творческие задания для учащихся: написать сочинение, подготовить доклады, составить альбомы, сделать спецвыпуски газет, составить гербарий и коллекции, подготовить раздаточные материалы для уроков, школьных выставок, музеев и т.п. Особое внимание в ходе этой беседы уделяется правилам поведения и основам техники безопасности. Факультативные и дополнительные занятия. Наряду с обязательными учебными занятиями в школах используются и разнообразные формы учебной работы, проводимой вне рамок учебных занятий (расписания уроков). Такие формы учебных занятий называются внеклассными или внеурочными. В первую очередь к внеклассным занятиям относятся факультативные занятия. Как самостоятельная форма организации текущей работы они появились в конце 60-х – нач. 70-х гг. во время проведения очередной реформы системы образования, затрагивающей в основном содержание школьного образования. Факультативные занятия представляют собой сверхпрограммные занятия, право выбора которых остается за учащимся, а посещение осуществляется на добровольной основе. Факультативные занятия призваны решать следующие задачи: - удовлетворять запросы учащихся в углубленном изучении отдельных учебных предметов; - развивать учебно-познавательные интересы и способствовать повышению познавательной активности; - способствовать развитию исследовательских умений, индивидуальныхособенностей, творческих способностей учащихся. Помимо учебных занятий, обязательных для всех учащихся, специально для слабоуспевающих учащихся проводятся дополнительные занятия. Дополнительными занятиями называют сверхпрограммные занятия с одним или группой учащихся по дополнительной отработке пройденного на уроках материала. Форма и время проведения дополнительных занятий жестко нерегламентируется. Это может быть занятие-консультация, на которой учитель еще раз излагает новый материал для тех, кто не понял его на уроке; или беседа с 2- 3 учащимися по тематике классной работы, в которую включено выполнение письменных заданий. Время таких занятий может быть и 20 мин, и 1 час.Возможно и выполнение учащимися самостоятельной работы. Другие формы внеклассной учебной работы. Принято считать, что внеклассная работа носит для учащихся добровольный характер и призвана удовлетворять их разнообразные познавательные и творческие запросы, а для их проведения не требуется полного состава класса. Считается также, что в них по собственному желанию могут участвовать учащиеся различных классов. К таким формам внеклассной учебной работы относят предметные кружки, научные общества, олимпиады, конкурсы и др. Предметные кружки и научные общества создаются на добровольных началах из учащихся одной параллели или же, если желающих немного, из учащихся соседних классов (5 – 6, 7 – 8 классов и т.д.). В них входят учащиеся, которые стремятся к расширению и обогащению своих знаний, имеющие склонность к рисованию, лепке, техническому творчеству, проведению опытной работы по биологии, химии, физике и т.д. Ведут работу кружков учителя-предметники. Кружковая работа включает в себя более углубленное изучение отдельных вопросов учебной программы, которые вызывают интерес учащихся. Содержанием их деятельности могут быть изучение новейших достижений науки и техники, опытная работа, моделирование, разработка проектов, ознакомление с жизнью и творческой деятельностью великих ученых, писателей, деятелей культуры. Общее представление о памяти, её физиологические основы. Процессы памяти. Виды памяти. Память — это форма психического отражения действительности, заключающаяся в запечатлении, сохранении, узнавании и воспроизведении следов прошлого опыта. Память обеспечивает целостность личности человека и его связь с прошлым опытом. 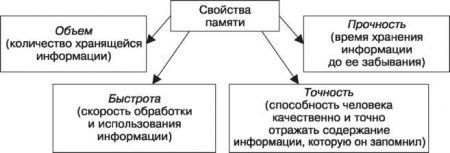 Вся воспринятая и запомненная информация распределяется между бесконечным множеством взаимосвязанных нейронов. Например, знания о том, что мы едим, как пахнет и выглядит еда и что мы с ней делаем, как покупаем ее, хранятся в отдельной зоне мозга каждое: форма — в зрительной коре головного мозга, тактильные ощущения — в премоторной и сенсорной областях, запах — в лобных долях и так далее. Эти зоны, называемые участками узнавания, располагаются в различных отделах мозга. В тот момент, когда нам необходимо узнать конкретный объект, например яблоко, эти участки перегруппировываются. Хотя воспоминания и не хранятся в конкретном месте, а распределены в системе нейронных связей, существует одна группа внутренних структур —лимбическая система, — от которой сильно зависит способ запоминания и архивирования информации. Она участвует в процессе консолидации памяти, связывая память с эмоциями. Лимбическая система располагается в глубине височных долей мозга и состоит из гиппокампа и миндалевидного тела. В процессе памяти также участвуют и другие участки мозга, например: лобные доли (помогают хранить и вызывать воспоминания); особая зона* в коре головного мозга (участвует в узнавании лиц); теменные доли (отвечают за запоминание простых задач); затылочные доли (хранят зрительную память); базальные ганглии и большой мозг (хранят память о привычках и моторных навыках); височные доли (хранят долговременные воспоминания); миндалевидное тело (воспроизводит воспоминания об эмоциональных событиях, например травматических и вызывающих страх) По способу запоминания память делится на: образную: слуховую, зрительную, вкусовую, обонятельную, тактильную, осязательную; моторная; эмоциональную; логическую. 3. Устные приемы сложения и вычитания в пределах 100, с переходом через десяток. Основные приемы вычислений используемые в пределах 100, рассматриваются при изучении темы «Сложение и вычитание в пределах 100» и постоянно находят применение при устных и письменных вычислениях в процессе решения примеров и задач. Навыки устных вычислений формируются в процессе выполнения учащимися разнообразных упражнений. Рассмотрим основные их виды: Нахождение значений математических выражений. Как известно, последовательность изучения отдельных случаев сложения и вычитания может быть различна, но традиционно учитывается прежде всего сложность вычислительных приемов: сначала рассматривают приемы, которые включают меньшее число операций, затем -- приемы, включающие большее число операций. Например, в сложении: сначала 36 + 2, затем 26 + 4, позже 26 + 7, аналогично -- в вычитании. Там, где возможно, приемы рассматриваются в сравнении: 36 + 2 и 36 + 20; приемы сложения чередуются с аналогичными приемами вычитания, которые вводятся в сопоставлении с рассмотренными только что приемами сложения. Таким образом, обеспечивается определенный перенос и дифференциация: 36 + 2, 36 + 20 и 36 - 2, 36 - 20; 26 + 4 и 30 - 7; 26 + 7 и 35 - 7. В хорошо подготовленном классе соответствующие приемы сложения и вычитания можно вводить одновременно -- так называемыми укрупненными дидактическими единицами. Методика работы, направленная на овладение детьми приемами вычислений, известна учителю. Вначале прием (способ действия) раскрывается с помощью соответствующего предметного действия (например, с пучками палочек и отдельными палочками или другими моделями десятков и единиц). Затем с опорой на иллюстрации дети решают пару примеров с подробной записью и устным пояснением, а после этого -- пару примеров с краткой записью и устным пояснением (обычно на первом уроке больше сделать не удается). На основе сравнения всех решенных примеров делается обобщение, как решать подобные примеры: единицы складывают с единицами, десятки -- с десятками. Далее для закрепления решают примеры с подробным и кратким пояснением приема и повторяют вывод. Поэтому аналогичные приемы вычитания дети «открывают» с большой долей самостоятельности. Решив с опорой на предметные наглядностей или иллюстрации пару новых примеров с объяснением вслух и сопоставив их с только что решенными примерами на сложение, дети без особых затруднений формулируют вывод: единицы вычитают из единиц, десятки -- из десятков. Затем переходят к решению примеров на сложение и вычитание, сравнивая приемы вычислений: 54 + 3, 54 - 3, 76 - 20, 76 + 20. Так как приходится прибавлять к одному из слагаемых, то, чтобы дети не забыли другое слагаемое, разрядные числа, составляющие двузначное число, рекомендуют подписывать под ним в следующей строке, соединяя числа проведенными от руки отрезками. Некоторые учителя говорят: «С записью чисел-помощников» -- и советуют детям (особенно тем, кто нуждается в этом) не только записывать разрядные числа, но и точкой отмечать то число, к которому прибавляют (из которого вычитают) в этом примере второе число. В классе, где особенно много слабо подготовленных детей, на этапе овладения приемами вычислений некоторые методисты рекомендуют использовать как записи, так и модели десятков и единиц: 36 + 20 = 56 Отметим, что на таких рисунках не следует использовать знаки арифметических действий. Вычислительный прием для случаев вида 26 + 4 включает сложение не только единиц, но и десятков. Рассматривая подробную запись, данную под примером, дети видят, что вначале складывают единицы, а затем полученный десяток прибавляют к десяткам. Выполняя краткую запись, можно объяснять короче. Например, решая пример 81 + 9, говорят: 81 -- это 80 и 1 (пишут под числом), к 1 прибавить 9, получится 10, 80 и 10 -- это 90. Сложение (вычитание) круглых десятков не надо объяснять вслух, так как к этому времени у детей уже сформировался навык подобных вычислений (т. е. эти действия выполняются свернуто в уме). Только в случае ошибки приходится объяснять даже давно изученный прием подробно и вслух. Для того чтобы у детей не произошло неверного обобщения (суммой заменяют всегда первое число), в данный урок в учебнике предлагается включить несколько примеров вида 60 + 18, 20 + 14, где второе число заменяют разрядными числами и, значит, удобнее сначала сложить десятки, а затем прибавить единицы. Решение таких примеров, кроме того, подготавливает детей к рассмотрению приема вычитания вида 60 - 24. Чтобы подготовить детей к овладению приемом для случаев вида 30 - 7, надо использовать специальные упражнения на замену чисел -- круглых десятков суммой по образцу: 50 = 40 + , 70 = + 10. В примерах вида 30 - 7 отсутствуют отдельные единицы. Но если дать детям в руки связанные в десятки палочки и спросить, как из 3 десятков вычесть 7 единиц, некоторые дети догадываются развязать 1 десяток и взять из него 7 палочек. Выполнив подробную запись этого приема, дети должны отметить, что и здесь единицы вычитают из единиц -- из 10 единиц, которые получают, заменяя уменьшаемое суммой чисел, одно из которых равно 10 [18, с.93]. Особое внимание надо обратить на вычитание нескольких единиц из 100. Например, 100 - 4. Объяснение: 100 -- это 90 и 10 (пишут под примером); вычитаем 4 из 10, получится 6; 90 да 6 -- получится 96. Новый прием полезно на этом же уроке сопоставить с рассмотренными ранее приемами: 76 + 4 и 80 - 4; 48 - 6 и 40 - 6, чтобы дети осознали его особенности. Прием вычислений для случаев вида 60 - 24 достаточно сложный и требует особого внимания. В отличие от предыдущих приемов, когда вычитали из одной части уменьшаемого и надо было не забыть прибавить другую часть, в новом приеме надо вычесть обе части -- и десятки, и единицы. Это хорошо видно детям, когда они выполняют предметные действия, например на палочках. Заметим, если используются модели чисел из треугольников и точек, то, изобразив уменьшаемое с помощью треугольников-десятков, надо на этом же рисунке зачеркнуть необходимое число десятков, а в одном из оставшихся треугольников изобразить 10 точек и зачеркнуть из них необходимое число единиц. На первом уроке полезно увеличить количество упражнений на основе предметных действий с подробным объяснением, а также рассмотреть примеры на сопоставление приемов (30 + 12 и 30 - 12) и затем обобщить: прибавляем и вычитаем по частям -- сначала десятки, потом единицы. На следующих уроках рассматриваются новые виды задач и обязательно закрепляются изученные приемы вычислений, особенно приемы вычитания, которые необходимо давать в сопоставлении. Например: 40 - 6 и 40 - 26; 67 - 30 и 60 - 37. Решать эти примеры полезно с подробным пояснением. Последними вводятся устные приемы сложения и вычитания с переходом через десяток вида 26 + 7 и 35 - 7. Сами приемы известны детям -- это прибавление и вычитание по частям так, чтобы после первого шага получились круглые десятки: 26 + 4 + 3, 35 - 5 - 2. В устные упражнения полезно включать задания на повторение состава однозначных чисел, а также на дополнение данных чисел до круглого числа. Например, дополни до 30 числа: 24, 26, 27, 28. Некоторые дети, хорошо знающие таблицу сложения, иногда предлагают другой прием: 26 + 7 = 20 + (6 + 7) = 20 + 13 = 33. Разумеется, не следует запрещать им вычислять таким образом. Однако вводить сразу два приема для всех учащихся на данном этапе нецелесообразно. Наблюдения показывают, что, познакомившись с приемом вычитания с переходом через десяток, многие дети делают неверный перенос этого приема на новые случаи (35 - 7, 7 - 5 = 2, 30 + 2 = 32). Прием, включающий получение круглого десятка (прибавление и вычитание по частям), как более известный детям, осваивается ими без особых затруднений и, кроме того, способствует закреплению табличного сложения и вычитания. Билет №13 Основные функции и назначение проверки и оценки знаний, умений и навыков. Формы проверки знаний. Система критериальной оценки знаний. Основными формами проверки знаний учащихся и студентов являются: коллоквиум, зачет, экзамен, контрольная работа, поурочное оценивание, тестирование, рейтинговое оценивание, выполнение квалификационных работ. Коллоквиум является формой текущего контроля. Он применяется для проверки знаний по определенному разделу (или объемной теме) и принятия решения о том, можно ли переходить к изучению нового материала. Коллоквиум — это беседа со студентами, целью которой является выявление уровня овладения новыми знаниями. В отличие от семинара главное на коллоквиуме — это проверка знаний с целью их систематизации. Коллоквиум может проводиться по вопросам, обсуждавшимся на семинарах. Конкретные вопросы для коллоквиума студентам не сообщаются, однако заранее формулируются преподавателем. Предполагаемый объем ответа не должен быть большим (примерно 1,5—2 мин), чтобы преподаватель мог успеть опросить всех студентов. Ответ студента на коллоквиуме всегда комментируется кратко: "верно - неверно". Па коллоквиуме не спрашивают по желанию. Для получения положительной оценки каждый студент должен ответить на два-три вопроса. В заключение студентам сообщаются оценки, которые для желающих комментируются. Зачет представляет собой форму проверки знаний, предусматривающую альтернативную оценку и соответственно бинарную отметку: "зачет" или "незачет". "Зачет" ставится в том случае, если студент выполнил задание, дал правильный ответ, усвоил учебный материал. "Незачет" ставится, если студент не выполнил задания, дал неправильный ответ, не усвоил материал. Важной задачей преподавателя является определение степени правильности выполнения задания (или ответа па вопрос), при которой может быть поставлен зачет. Во избежание взаимного непонимания между преподавателем и студентами необходимо четко определить эти критерии и довести их до сведения обучающихся. Зачет предназначен прежде всего для оценки выполнения заданий практического характера, поэтому он может использоваться для зачитывания факта сдачи определенных тем курса, лабораторных и практических работ. Зачет используется также для оценки успешности прохождения студентами лабораторного практикума, курса практических занятий. В этом случае существенно то, что студент прошел данный учебный курс, а качество его знаний в данном случае не оценивается. Однако преподаватель должен четко определить, каким должно быть минимальное количество выполненных заданий или лабораторных работ и минимальный объем знаний, при котором студент получит зачет по курсу. Зачет иногда используется для оценки знаний по курсу, содержащему теоретический материал. Обычно это бывает связано с формальными ограничениями, накладываемыми на количество экзаменов, допускаемых в одну сессию, что снижает степень дифференцированности в оценке усвоения студентами знаний по учебному курсу, поскольку используется бинарная отметка. Для преодоления этого недостатка порой вводится особая форма — дифференцированный зачет, при котором применяется балльная отметка. Следует признать, что зачет — более простая для преподавателя форма оценки, поскольку требует дифференциации между двумя отметками: "зачет" и "незачет". Экзамен требует от преподавателя более сложной дифференциации между несколькими градациями отметок: "отлично" (5), "хорошо" (4), "удовлетворительно" (3), "неудовлетворительно" (2), а в школьной практике еще и "очень плохо" (1). Преподавателю обычно предоставляется определенное учебное время для проведения зачета по курсу. Однако использоваться оно может или для однократной процедуры принятия зачета по всему курсу, или для проверки и зачитывания отдельных работ. В последнем случае зачет по курсу в целом выставляется по совокупности зачтенных практических работ и выполненных заданий. Экзамен представляет собой форму проверки знаний, предусматривающую дифференцированную оценку и соответственно отметку, имеющую несколько градаций. В школьной практике России это пятибалльная система отметок: 5, 4, 3, 2, 1. До 1944 г. они обозначались словами: "отлично", "хорошо", "удовлетворительно", "плохо", "очень плохо". В вузовской системе России это четырех-балльная система, в которой используются словесные отметки "отлично", "хорошо", "удовлетворительно", "неудовлетворительно". В других странах нередко применяются другие обозначения, а аналогичные баллы могут иметь другие значения. Также могут использоваться буквы: А, В, С, О. Для увеличения дифференцирующей способности системы отметок могут использоваться знаки "+" (плюс) или "-" (минус). В США во многих университетах они используются официально Понятие о деятельности. Виды деятельности. |
