пособие. ТТД ч1 учебное пособие. Техническая термодинамика

• Название: Техническая термодинамика
• Анкор: пособие
• Дата: 02.02.2023
• Размер: 4.15 Mb.
• Имя файла: ТТД ч1 учебное пособие.doc
• Тип: Учебное пособие; #917693
• страница: 13 из 19

Адиабатный процесс

В тепловых машинах, таких как турбина или насос, процесс протекает очень быстро и теплообмен с внешней средой очень незначителен, им можно пренебречь. Поэтому обратимым процессом в таких машинах является идеальная адиабата (изоэнтропа).

На рис. 6.24, 6.25, 6.26 изображен обратимый адиабатный процесс расширения пара 12 в Р,v-, T,s- и h,s- диаграммах.

В Р,v- диаграмме адиабата представляет собой кривую гиперболического характера с переменным показателем адиабаты "к". Необходимо отметить, что показатель адиабаты "к" для воды и пара никакого отношения к коэффициенту Пуассона c_p/c_v не имеет. Он рассчитывается только по параметрам обратимого адиабатного процесса вблизи какой - либо фиксированной точки по формуле




Рис. 6.24. Адиабатный процесс пара в P,v - диаграмме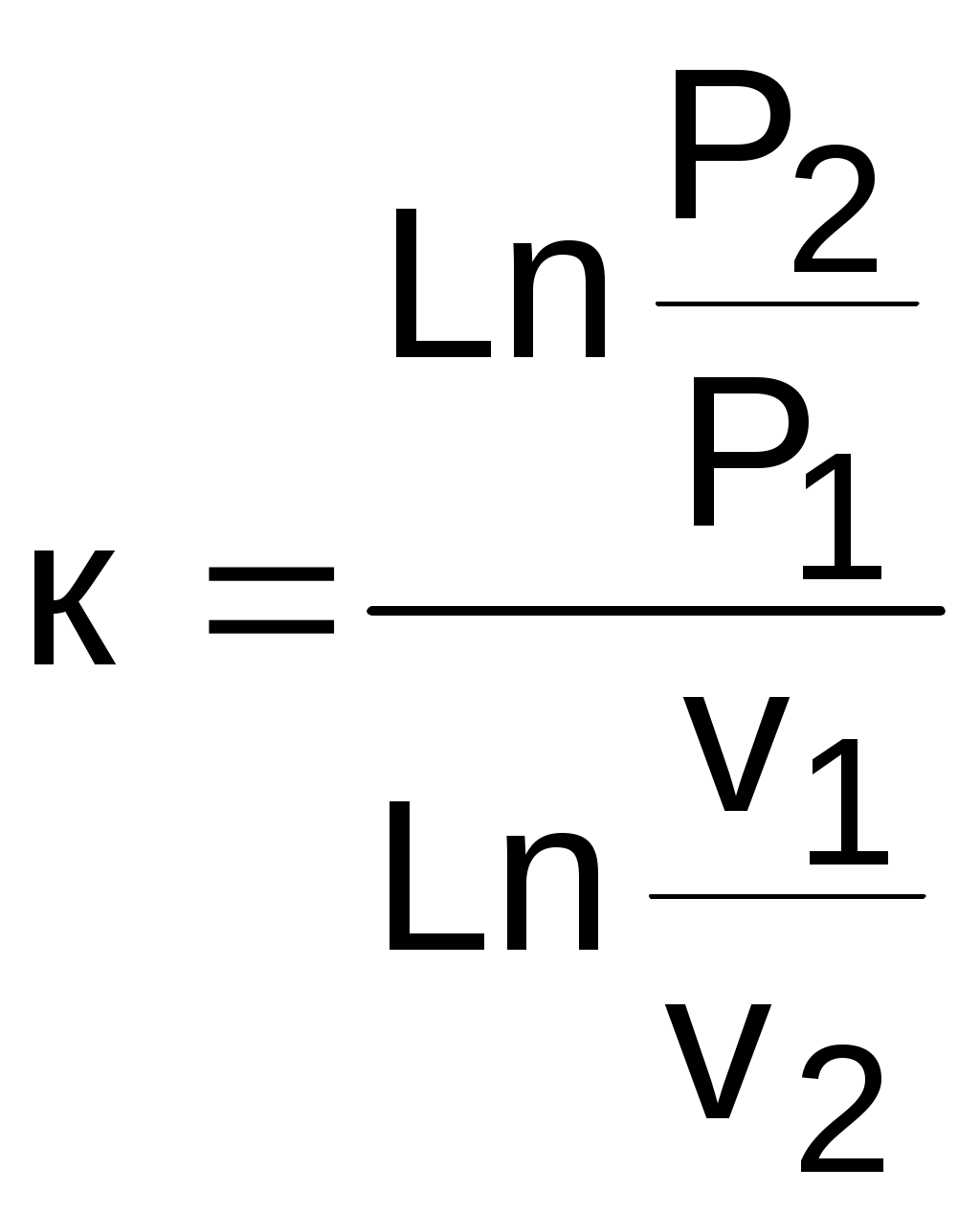


. (6.30)

Показателем адиабаты в расчетах процесса пользуются крайне редко ввиду того, что он – величина переменная. Его численные значения сильно отличаются друг от друга в различных точках адиабатного процесса: чем дальше расположены точки, тем больше разница. При переходе процесса из области перегретого пара в область влажного насыщенного эта разница еще больше увеличивается.

Площадь под процессом 12 в Р,v- диаграмме есть работа расширения, а поскольку q_s = 0, то работа расширения адиабатного процесса равна изменению внутренней энергии с обратным знаком и может быть подсчитана как

_s = u₁ - u₂ = (h₁ - h₂) - (Р₁v₁ - Р₂v₂) . (6.31)

В формуле (6.31) при расчетах следует обратить внимание на соответствие единиц измерения энтальпий и произведений Pv.

В Т,s- и h,s- диаграммах обратимый адиабатный процесс представляет вертикальную прямую (s=const – изоэнтропа). Представление энергетических характеристик (_s, u) в Т,s- и h,s- диаграммах возможно с помощью дополнительных построений, но это не имеет практической ценности. В h,s- диаграмме разность энтальпий адиабатного процесса представляет работу изменения давления в потоке _о = h₁ - h₂ (техническая работа в турбине, насосе и т.п.). С понятием этой работы познакомимся позднее при изучении процессов теплоэнергетических установок.

Изохорный процесс

Изохорный процесс может иметь место в случае теплообмена с внешней средой водяного пара, находящегося в сосуде постоянного объема. На рис. 6.27, 6.28, 6.29 изображен изохорный процесс 12 в Р,v-, T,s-, h,s- диаграммах.

В Р,v- диаграмме изохора 12 – вертикальная прямая (рис.6.27). Работа расширения в изохорном процессе равна нулю (=Рdv, dv=0, _v=0). Теплота изохорного процесса расходуется только на увеличение внутренней энергии пара:

q_v = u₂ - u₁ = h₂ - h₁ -v(Р₂ - Р₁) . (6.32)




В диаграмме Т,s теплота q_v изображается площадью под изохорным процессом 12 (рис. 6.28). Эта же площадь соответствует изменению внутренней энергии изохорного процесса. Поскольку s₂ > s₁, теплота и изменение внутренней энергии процесса 12 положительные.

По диаграмме h,s можно определить все необходимые параметры состояния (рис. 6.29) для расчета теплоты и изменения внутренней энергии изохорного процесса.

Изобарный процесс

На рис. 6.30, 6.31, 6.32 изображен изобарный процесс 12 в Р,v-, T,s-, h,s- диаграммах. В точке 1 этого процесса водяной пар находится в области влажного насыщенного пара, поэтому его состояние может быть задано любой парой параметров, кроме Р₁ и t₁, так как в этой области изобара совпадает с изотермой. Вторая точка процесса находится в области перегретого пара и состояние пара здесь определяется любой парой параметров.

В диаграмме Р,v изобара представляет горизонтальную прямую 12 (рис. 6.30), площадь под которой соответствует работе изменениия объема, определяемой по формуле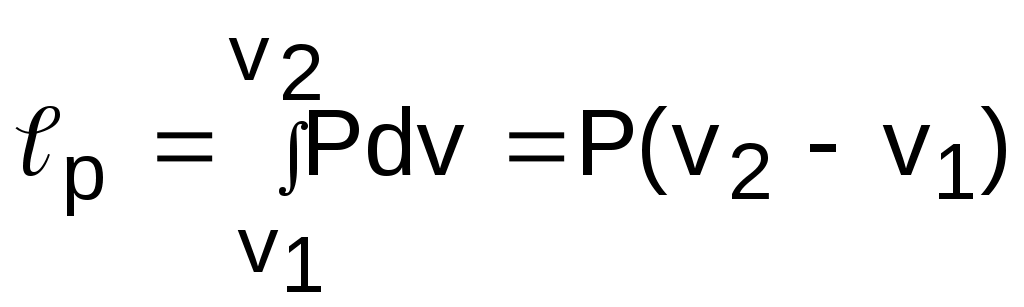

. (6.33)

Количество теплоты в изобарном процессе соответствует изменению энтальпии (q = dh - vdР, dР = 0, dq_p = dh_p) и определяется как

q
_p = h₂ - h₁. (6.34)

В


Рис. 6.31. Изобарный процесс в T, s - диаграмме


Рис. 6.32. Изобарный процесс в h, s - диаграмме

Т,s- диаграмме (рис. 6.31) теплота q_p представлена площадью под процессом, в h,s- диаграмме (рис. 6.32) – отрезком прямой в виде разности ординат. Изменение внутренней энергии изобарного процесса подсчитывается по формуле

u₂ - u₁ = (h₂ - Рv₂) -(h₁ - Рv₁) = h₂ - h₁ - Р(v₂ - v₁) = q_p - _p . (6.35)
Изотермический процесс

На рис. 6.33, 6.34, 6.35 изображен изотермический процесс 12 в Р,v-, T,s-, h,s- координатах. Определение параметров в начальной и конечной точках процесса аналогично предыдущим процессам.

Работа расширения изотермического процесса изображается площадью под процессом 12 в Р,v- координатах (рис. 6.33) и рассчитывается исходя из первого закона термодинамики:


_т = q - (u₂ - u₁). (6.36)

В
Т,s- диаграмме изотерма – горизонтальная прямая. Площадь под изотермическим процессом 12 в T,s- диаграмме представляет теплоту (рис. 6.34), которая может быть подсчитана по формуле

q_т = T(s₂ - s₁). (6.37)

В h,s- диаграмме (рис. 6.35) изотерма 12 – сложная кривая линия в области влажного пара, совпадающая с изобарой. Подсчет изменения внутренней энергии изотермического процесса ведется традиционным для водяного пара образом, через энтальпию:

u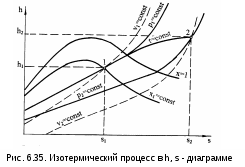
₂ - u₁ = h₂ - h₁ - (Р₂v₂ - Р₁v₁).

7. ВЛАЖНЫЙ ВОЗДУХ
Влажный воздух – это смесь сухого воздуха и водяного пара. В воздухе при определенных условиях кроме водяного пара может находиться его жидкая (вода) или кристаллическая (лед, снег) фаза. В естественных условиях воздух всегда содержит водяной пар.
7.1. Основные характеристики влажного воздуха

Влажный воздух можно рассматривать как смесь сухого воздуха и водяного пара (жидкую и твердую фазы воды в воздухе пока считаем отсутствующими).

Используя законы для смесей газов, получим, что давление влажного воздуха равно сумме парциальных давлений сухого воздуха и водяного пара:

Р = Р_в + Р_п . (7.1)

Для наглядности представления основных характеристик влажного воздуха изобразим в Р,v- диаграмме (рис.7.1) состояния водяного пара во влажном воздухе. В качестве определяющих параметров водяного пара во влажном воздухе используются температура воздуха t
и парциальное давление водяного пара Р_п.

Водяной пар во влажном воздухе может находиться в трех состояниях (рис.7.1): точка 1 – перегретый пар, точка 2 – сухой насыщенный пар, точка 3 – влажный насыщенный пар (сухой насыщенный пар плюс капельки жидкости в состоянии насыщения). Высшим пределом парциального давления водяных паров при данной температуре воздуха t является давление насыщения пара Р_{п max} = Р_н.

Абсолютная влажность  – это массовое количество водяных паров в одном кубическом метре влажного воздуха. Для ее определения используется величина, обратная удельному объему водяного пара при Р_п и t, =1/v (кг/м³). Действительно, по закону Дальтона водяной пар занимает весь объем смеси, а его плотность соответствует массе водяного пара в одном кубическом метре влажного воздуха.

Необходимо отметить, что абсолютная влажность воздуха характеризует содержание в воздухе только одной – паровой фазы воды.

Относительная влажность  – это отношение абсолютной влажности к максимально возможной влажности воздуха при данной температуре:

, (7.2)

где " и v" – максимальная абсолютная влажность воздуха и удельный объем сухого насыщенного водяного пара при данной температуре t.

Относительная влажность воздуха характеризует потенциальную возможность воздуха испарять влагу и забирать в себя пар из окружающей среды при данной температуре.

Максимальное содержание пара в воздухе соответствует состоянию точки 2 в Р,v- диаграмме (см. рис.7.1), где пар сухой насыщенный. При переходе в область влажного пара при данной температуре t (точка 3) в воздухе количество сухого насыщенного пара остается постоянным (такое же, как в точке 2) (для паровой фазы воды в этом случае удельный объем остается неизменным, v"=const, и минимально возможным при данной температуре воздуха), только к нему добавляются капельки воды в состоянии насыщения.

Различают 3 состояния влажного воздуха.

1. Ненасыщенный влажный воздух – <100 %, Р_п<Р_н, <", водяной пар во влажном воздухе в виде перегретого пара (точка 1).

2. Насыщенный влажный воздух – =100 %, Р_п=Р_н, =", водяной пар во влажном воздухе в виде сухого насыщенного пара (точка 2).

3. Перенасыщенный влажный воздух– =100 %, Р_п=Р_н, =", кроме сухого насыщенного пара в воздухе находятся капельки воды в состоянии насыщения или льда, снега (точка 3 при наличии капелек воды).

В технике используется такая характеристика влажного воздуха, как температураточки росы. Это такая температура, начиная с которой при охлаждении влажного воздуха при постоянном давлении из него начинается выпадение капелек воды (соответствует температуре точки А процесса 1А, рис. 7.1). При снижении температуры воздуха ниже температуры точки росы при постоянном давлении всей смеси и постоянном содержании в ней H₂О (процесс АВ) парциальное давление водяного пара уменьшается (Р_вп<Р_п), количество сухого насыщенного пара уменьшается, а количество капелек воды увеличивается. В этом случае в P,v- диаграмме процесс АВ пойдет в области влажного пара с уменьшением степени сухости по мере снижения температуры.
7.2. Характеристики атмосферного влажного воздуха

При температурах атмосферного воздуха 0-50 ^оС парциальное давление водяного пара очень мало (0,006-0,07 бар), что позволяет применить к перегретому и сухому насыщенному водяному пару уравнение идеального газа:

Р_пv = RT, (7.3)

Р_нv" = RT, (7.4)

где Р_п, Р_н и v, v" – парциальные давления и удельные объемы для перегретого и сухого насыщенного водяного пара при температуре Т.

Разделив эти выражения друг на друга, получим расчетное выражение относительной влажности воздуха через парциальные давления водяного пара: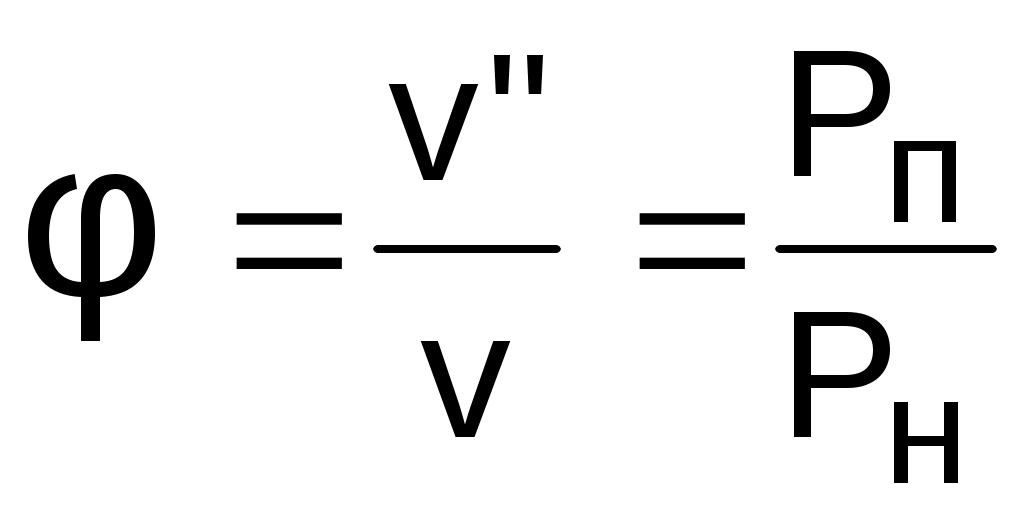

. (7.5)

Молярная масса атмосферного влажного воздуха определяется по уравнению для смеси газов:

 = r_в_в + r_п_п, (7.6)

где r_в, r_п – объемные доли сухого воздуха и водяного пара,

r_в = Р_в/Р=(Р - Р_п)/Р; r_п = Р_п/Р,

Р, Р_в и Р_п – атмосферное и парциальные давления сухого воздуха и водяного пара;

_в, _п – молярные массы сухого воздуха и водяного пара,

_в=28,96 кг/кмоль, _п=18,016 кг/кмоль.

В результате подстановки численных значений молярных масс сухого воздуха и водяного пара в выражение (7.6) получаем расчетное выражение молярной массы влажного воздуха в виде

. (7.7)

Молярная масса влажного воздуха меньше молярной массы сухого воздуха.

Газовая постоянная влажного воздуха определяется выражением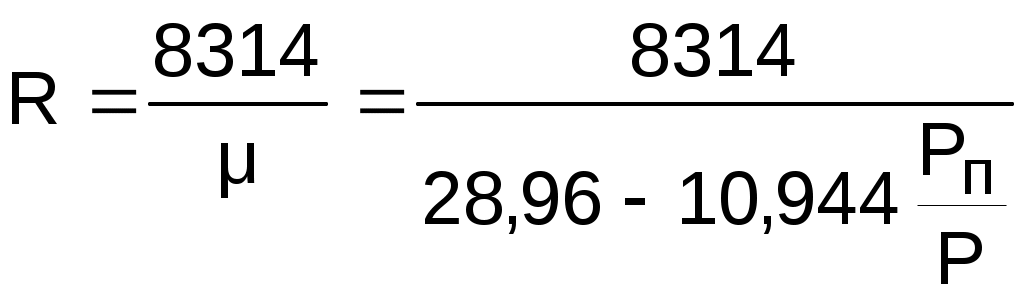

, (7.8)

она больше газовой постоянной сухого воздуха.

Плотность влажного воздуха определяется выражением

, (7.9)

она меньше плотности сухого воздуха, т.е. влажный воздух легче сухого воздуха.

Влагосодержание d – это масса водяного пара в граммах, приходящаяся на 1 кг сухого воздуха. В общем случае понятие "влагосодержание" относится не только к паровой фазе воды, но и к жидкой, и к твердой ее фазам. Расчетное выражение для влагосодержания паровой фазы воды в воздухе (г/кг с.в.) получается из соотношения

(7.10)

путем замены отношений масс на массовые доли и выражения последних через объемные доли, которые представляют отношения соответствующих парциальных давлений к давлению всей смеси:

, (7.11)

где g_п, g_в – массовые доли пара и сухого воздуха;

r_п, r_в – объемные доли пара и сухого воздуха.

Энтальпия влажного воздуха Н рассчитывается на 1 кг сухого воздуха (кДж/кг с.в.) и определяется как сумма энтальпий компонентов, находящихся в 1 кг сухого воздуха:

, (7.12)

где d_п, d_ж, d_т – количество пара, жидкости и твердой фазы Н₂О (лед, снег) в граммах на 1 кг сухого воздуха (влагосодержания);

h_в, h_п, h_ж, h_т – удельные энтальпии сухого воздуха, пара, жидкости и твердой фазы Н₂О, кДж/кг.

В выражении (7.12) энтальпии всех компонентов влажного воздуха необходимо подставлять при одинаковых давлениях и температурах начала их отсчета.

Для атмосферного влажного воздуха удельные энтальпии всех компонентов можно рассчитать, приняв ряд допущений, которые не приведут к погрешностям инженерных расчетов в диапазоне изменения атмосферного давления и температуры от -40 до 150 ^оС более чем на 0,5 %.

Эти допущения сводятся к следующему.

Начало отсчета удельной энтальпии сухого воздуха принимают при t_о=0 ^оС и считают, что энтальпия сухого воздуха зависит только от температуры (как для идеального газа), а его изобарная теплоемкость – величина постоянная. Расчетное выражение удельной энтальпии сухого воздуха в этом случае будет соответствовать соотношению

h_в = h_в - h_во = c_рв(t - 0) = с_рвt , (7.13)

где h_во = 0 – начало отсчета энтальпии сухого воздуха при 0 ^оС;

c_рв = 1 кДж/(кг∙К) – изобарная теплоемкость идеального сухого воздуха, принята постоянной.

При таких допущениях удельная энтальпия сухого воздуха (кДж/кг) численно равна его температуре в градусах Цельсия:

h_в = t .

Для определения энтальпии воды и водяного пара начало отсчета внутренней энергии u_о = 0 принято при параметрах тройной точки воды (t_o=0,01 ^оС и Р_o=611,2 Па) на линии насыщения х=0. При этих параметрах численное значение энтальпии h_о' = P_ov_o' = 0,000611 кДж/кг представляет очень малую величину, которую для наших расчетов можно принять равной нулю. Таким образом, можно считать, что начало отсчета энтальпии H₂О, как и сухого воздуха, ведется от 0 ^оС и ее численное значение при этой температуре равно нулю (h_по=0).

Для дальнейшего пояснения определения энтальпии водяного пара рассмотрим изобару Р_o, соответствующую тройной точке воды в Т,s- диаграмме (рис.7.2). Площадь ЕС11'0Е под изобарой Е1 представляет в T,s- диаграмме теплоту изобарного процесса, состоящую из теплоты парообразования и теплоты перегрева пара, которая рассчитывается как разность энтальпий:

h_п1 - h_по = r_о + q_п1.

Поскольку энтальпию в тройной точке воды (точка Е) мы приняли за нуль, то абсолютное значение удельной энтальпии пара в точке 1 определяется выражением

h_п1 = r_o + q_п1 ,

где r_o = 2501 кДж/кг – теплота парообразования воды при 0 ^оС;

q_п1 – теплота перегрева пара от Т_о до Т.

Приняв изобарную теплоемкость перегретого пара величиной постоянной, c_рп=1,93 кДж/(кг∙К), что допустимо для интервала температур атмосферного воздуха, получим расчетное выражение теплоты перегрева пара (кДж/кг):

q_п1 = с_pп(t - 0) = 1,93t .

В результате этих преобразований расчетное выражение энтальпии водяного пара при температуре t и давлении тройной точки воды Р_o примет вид (кДж/кг)

h_п1 = 2501 + 1,93t .

Этим выражением можно пользоваться и для расчета энтальпий пара при давлениях, отличных от давления тройной точки воды. Это объясняется тем, что при атмосферных условиях парциальные давления пара малы и близки к давлению тройной точки воды. При Р_п>Р_о (соответствует состоянию пара в точке 2, рис.7.2) энтальпия пара будет представлять сумму трех слагаемых:

h_п = q' + r + q_п ,

г
де q' – изобарная теплота нагрева воды от 0 ^оС до состояния насыщения (площадь ЕВВ'0Е).

Энтальпии пара h_п соответствует площадь под изобарой ЕВ2. По сравнению с площадью под изобарой Е1 здесь присутствует теплота q', но величины r и q_п уменьшились по сравнению с величинами r_o и q_п1. При малых отклонениях изобар от изобары тройной точки воды в выражении для h_п по сравнению с выражением для h_п1 будет происходить взаимная компенсация уменьшения величин r и q_п за счет увеличения величины q'. В соответствии с рис. 7.2 эту взаимную компенсацию составляющих энтальпий h_п и h_п1 можно представить равенством площадей 11'2'D1 и 2DCЕВ2, т.е. будет справедливо равенство энтальпий h_п1 и h_п. На основании этого равенства получается расчетное выражение для энтальпии пара в атмосферном влажном воздухе:

h_п = r_o + q_п1 = q' + r + q_п = 2501 + 1,93t . (7.14)

Для определения энтальпии жидкой фазы воды принимают постоянной ее изобарную теплоемкость, что допустимо при параметрах атмосферного воздуха. Исходя из этого допущения расчетное выражение энтальпии жидкой фазы воды будет представлено в виде уравнения

h_ж = h_ж - h_по = с_рж(t - 0) = 4,187t , (7.15)

где с_рж = 4,187 кДж/(кг∙К) – изобарная теплоемкость воды.

Для определения энтальпии твердой фазы воды (лед, снег) принимаются постоянными удельная теплота плавления льда и его изобарная теплоемкость. Эти величины берутся при параметрах тройной точки воды. Такие допущения возможны, поскольку в соответствии с Р,t- диаграммой для воды (рис.7.3) имеют место следующие факты:

• 
  в атмосферном воздухе твердая фазы воды (т.ф.) может присутствовать только при температурах и парциальных давлениях пара, меньших (или равных) температуры и давления тройной точки воды, т.к. только на линии сублимации АС возможно одновременное существование паровой и твердой фаз воды;
  
• 
  плавление льда в атмосферном воздухе возможно только при температуре 0 ^оС;
  
• 
  переход льда в паровую фазу при температурах меньше 0 ^оС происходит, минуя жидкую фазу воды, – по линии сублимации (АС);
  
• 
  п арциальное давление водяного пара при отрицательных температурах атмосферного воздуха ненамного меньше (или равно) давления тройной точки воды Р_о, следовательно, теплота изобарного охлаждения твердой фазы воды от 0 ^оС может быть рассчитана по изобаре Р_о.
  

Энтальпия льда будет величиной отрицательной, поскольку начало отсчета энтальпии идет от температуры 0 ^оС жидкой фазы воды, а температура льда всегда меньше или равна 0 ^оС. Расчетное выражение энтальпии твердой фазы воды (льда, снега) в атмосферном воздухе представляет собой сумму удельной теплоты плавления льда, взятой с отрицательным знаком, и удельной изобарной теплоты охлаждения льда от t=0 ^оС до отрицательной температуры t:
h_т = -  + с_рт(t - 0) = -335 + 2,1t , (7.16)

где  = 335 кДж/кг – удельная теплота плавления льда при t=0 ^оС;

с_рт = 2,1 кДж/(кг∙К) – изобарная теплоемкость льда; взята при давлении тройной точки воды и принята величиной постоянной.

В результате всех вышеприведенных упрощений окончательное расчетное выражение энтальпии влажного атмосферного воздуха (кДж/кг с.в.) примет вид

. (7.17)

Психрометр

Это прибор для определения влагосодержания атмосферного воздуха. Он состоит из двух термометров: сухого и мокрого (рис.7.4). Мокрый термометр обернут тканью, смачиваемой водой.

Сухой термометр показывает температуру t атмосферного влажного воздуха. Мокрый термометр показывает температуру t_м, которая в большинстве случаев меньше температуры сухого термометра. Понижение температуры t_м по отношению к температуре t вызвано испарением воды из ткани. Однако t_м будет больше температуры точки росы вследствие наличия теплообмена влажной ткани с окружающей средой, имеющей температуру t>t_м.

П ри насыщенном влажном воздухе вода не может испаряться из ткани и t=t_м. При ненасыщенном влажном воздухе t>t_м. Чем суше воздух, тем больше разность температур t-t_м и тем меньше его влагосодержание. Зависимость влагосодержания d_п для атмосферного воздуха от t и t_м устанавливается экспериментально. Результаты этих испытаний сводятся в психрометрические таблицы, которыми пользуются для определения влагосодержания воздуха по показаниям температур психрометра.
7.3. H,d- диаграмма атмосферного влажного воздуха

Для упрощения определения параметров атмосферного влажного воздуха используют H,d- диаграммы влажного воздуха. Они строятся для постоянного давления воздуха (обычно Р=745 мм рт.ст.), но поскольку парциальное давление водяного пара на несколько порядков меньше давления влажного воздуха, а атмосферное давление изменяется в небольших пределах, то, с достаточной для инженерных расчетов степенью точности, ими можно пользоваться и при других атмосферных давлениях воздуха.

Построение H,d- диаграммы влажного воздуха основано на расчетном выражении энтальпии атмосферного влажного воздуха:

.

Построение H,d- диаграммы в прямоугольной системе координат не выполняется. Это объясняется большим углом наклона изотерм к оси d в прямоугольной системе координат для области ненасыщенного влажного воздуха. Тангенс их угла наклона к оси d определяется выражением (H/d)_t=(2501+1,937t)/1000, что соответствует углу, близкому к 90^о (рис.7.5). В такой системе координат все изотермы в области ненасыщенного влажного воздуха будут располагаться очень близко друг к другу и к оси H. Работа с такой диаграммой практически невозможна.

H ,d- диаграмму выполняют в косоугольной системе координат, как правило, с углом между осями H и d в 135^о. Это позволяет увеличить по сравнению с прямоугольной системой координат расстояние между изотермами и линиями других характеристик ненасыщенного влажного воздуха в H,d- диаграмме.

Рассмотрим принцип построения линий, изображенных на H,d- диаграмме влажного воздуха (рис.7.6). Ось координат влагосодержаний d имеет нулевое начало. Вертикальные линии в H,d- диаграмме представляют линии постоянных влагосодержаний d=const. Линии постоянных энтальпий H=const параллельны оси d и идут под углом 135^о к оси H.