пособие. ТТД ч1 учебное пособие. Техническая термодинамика

• Название: Техническая термодинамика
• Анкор: пособие
• Дата: 02.02.2023
• Размер: 4.15 Mb.
• Имя файла: ТТД ч1 учебное пособие.doc
• Тип: Учебное пособие; #917693
• страница: 12 из 19

6.3. Жидкость на линии фазового перехода

В теплоэнергетических установках вода используется в двух фазовых состояниях: в виде пара и жидкости. Поэтому в дальнейшем будем рассматривать только эти две фазы воды.

В технических расчетах абсолютные величины энергетических параметров (энтропия, внутренняя энергия, энтальпия) не имеют принципиального значения. Поэтому допустима свобода выбора начала отсчета этих параметров. Необходимо, конечно, учитывать аналитические связи этих величин между собой и с другими термодинамическими параметрами. Например, энтальпия и внутренняя энергия при одинаковых Р_о и t_о, взятых за начало отсчета для u_о, будут разными числами (h_о>u_o).

Для воды в качестве опорной точки принята тройная точка [11]. При давлении и температуре тройной точки Р_о = 611,2 Па и Т_о = 273,16 К приняты равными нулю энтропия и внутренняя энергия жидкой фазы воды (на линии х=0), соответствующее этим параметрам значение энтальпии h_о'=0,614 Дж/кг (это энтальпия на линии х=0). Все параметры на линии насыщения жидкой фазы воды обозначаются с одним штрихом.

При давлениях, применяемых в технических устройствах, жидкость можно считать несжимаемой, т.е. с постоянным объемом, не зависящим от давления. Следовательно, расстояние между молекулами жидкости будет зависеть только от температуры, а внутренняя энергия жидкости будет функцией только одного параметра – температуры, т.к. кинетическая и потенциальная ее составляющие определяются только температурой. Таким образом, с достаточной степенью точности для технических расчетов можно считать, что при 0 ^oС (273,15 К) внутренняя энергия жидкости, независимо от давления, равна нулю. Здесь отождествляется t=0 ^oС с температурой тройной точки воды, а изотерма при t=0 ^oС в области жидкой фазы будет выступать в качестве левой пограничной кривой жидкой фазы.

Рассмотрим процесс нагрева жидкости от нулевой температуры до температуры насыщения при заданном давлении Р=const в Р,v- и T,s- диаграммах (рис. 6.10 и 6.11). Целью анализа этого процесса будет представление методики определения энергетических параметров жидкости на линии насыщения х=0 и ее изобарной теплоемкости: h', u', s', c_p'. Экспериментально можно определить только зависимость температуры, давления и удельного объема друг от друга, а также замерить количество теплоты процесса. Поэтому энергетические параметры и теплоемкость процесса являются расчетными величинами.

Для нагрева жидкости от t=0 ^oС до температуры насыщения t_н при заданном давлении Р (процесс 12) ей нужно сообщить количество теплоты

, (6.4)

где c_p – изобарная теплоемкость жидкости;

u_о' и u' – внутренняя энергия жидкости при t=0 ^oС и t_н;

v_о' и v' – удельный объем жидкости при t=0 ^oC и t_н.

Все величины в выражении (6.4) взяты на линии насыщения х=0.

Подогрев жидкости от t=0 ^oС до t_н, соответствующей давлению Р, можно осуществить по изобаре 12 и по линии 1М2 (см. рис. 6.10) в Р,v- диаграмме, а в T,s- диаграмме (см. рис. 6.11) точки 1 и М совместятся и процесс 1М2 пойдет по пограничной кривой х=0. В обоих случаях изменение внутренней энергии одно и то же, а работа расширения процесса 12 отличается от работы расширения процесса 1М2 на заштрихованную площадь 12М1 в Р,v- диаграмме. Разница в затратах теплоты, при нагреве жидкости по изобаре и по пограничной кривой x=0 (рис. 6.11), обусловлена разностью работ. Эта разница работ составляет практически неощутимую величину, т.к. работа изменения объема очень мала по сравнению с изменением внутренней энергии жидкости (объем жидкости меняется очень незначительно). Так, при давлении 20 бар при нагреве жидкости от t = 0 ^oС до t_н = =212,37 ^oС общая затрата теплоты составляет 906,6 кДж/кг, а на долю работы расширения приходится 0,355 кДж/кг, т.е. менее 0,04 %. Следовательно, нагрев жидкости в основном определяется изменением внутренней энергии, которое зависит практически только от изменения температуры.

Таким образом, теплоемкость жидкости с_p=dq'/dt в основном зависит от температуры, и часто в инженерных расчетах она принимается как функция только одного параметра – температуры. Это подтверждается и экспериментальными данными: так при t=90 ^оС удельная изобарная теплоемкость жидкости при давлении 1 бар равна 4,205 кДж/(кг·К), а при давлении 50 бар – 4,194 кДж/(кг·К), что соответствует 0,26 % относительной разности этих теплоемкостей.

Количество теплоты q', затраченное на нагрев 1 кг жидкости от t=0^oС доt_н при заданном постоянном давлении, называется теплотой жидкости. Так как это теплота изобарного процесса, она соответствует разности энтальпий:







0


q' = h' - h_о, (6.5)

где h_о и h' – энтальпии жидкости при 0 ^oС и на линии насыщения х=0 при заданном давлении.

Поскольку h_о = u_о + Рv_о, а u_о=u_о'=0 и v_o'=v_o (при всех давлениях жидкости), равенство (6.5) можно записать как

q' = h' - Рv_o'. (6.6)

Величина Рv_о' очень мала по отношению к q', и при невысоких давлениях можно принимать q'  h'. Внутренняя энергия жидкости на линии насыщения рассчитывается по энтальпии

u' = h' - Рv'. (6.7)

Исходя из выражений (6.6) и (6.7) и того, что v'>v_о', получим соотношение h'>q'>u'. При небольших давлениях (до 100 бар) разница между этими тремя величинами h', q', u' очень мала. Например, при давлении 100 бар эта разница не превышает 10 кДж/кг.

Исходя из вышеизложенного энтальпию жидкости на линии насыщения х=0 можно определить как сумму h'=q'+Рv_o'. В свою очередь, теплоту жидкости q' определяют экспериментально или рассчитывают по заранее найденной зависимости изобарной теплоемкости жидкости от температуры при заданном давлении. При давлениях до 10 бар изобарная теплоемкость жидкости мало зависит от температуры и давления и в приближенных расчетах может приниматься постоянной и равной 1 ккал/(кг·К) или 4,187 кДж/(кг·К).

Энтропия жидкости на линии насыщения x = 0 определяется исходя из принятого условия ее равенства нулю в тройной точке воды (s_о'=0). С изменением давления энтропия жидкости при температуре тройной точки (или 0 ^oС) s_о изменяется, однако это изменение очень незначительное. Поскольку энтропия, как любой параметр состояния, является функцией двух независимых параметров состояния, а при t=0 ^оС для всех давлений жидкости внутренняя энергия жидкости практически равна нулю, то и энтропия жидкости при t=0 ^оС для всех давлений будет практически постоянной и равной энтропии жидкости в тройной точке воды, т.е. s_о=0. Так при давлении 22 МПа и t=0 ^оС s_о=0,0009 кДж/(кг·К), а при давлении 1 кПа энтропия жидкости на линии насыщения s'=0,106 кДж/(кг·К), т.е. энтропия жидкости при t=0 ^оС несоизмеримо мала по сравнению с энтропией жидкости в состоянии насыщения для всех давлений, используемых в практической деятельности.

Зная значение энтропии s_о при t=0 ^oС и заданном давлении, энтропию жидкости на линии насыщения при T_н можно определить как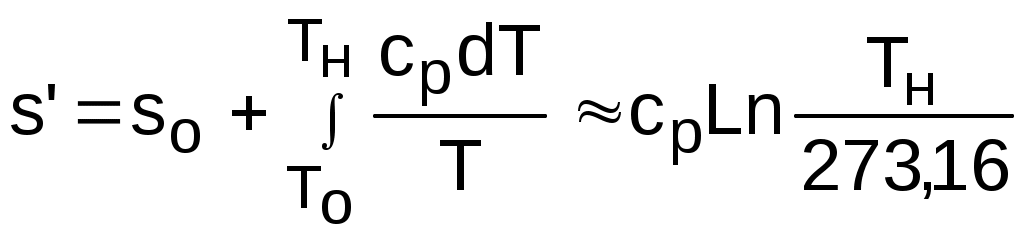

, (6.8)

где s_о = s_о'= 0 – при давлениях, используемых в технике;

с_p  4,187 кДж/(кг·К) – при умеренных давлениях.

В точных расчетах надо пользоваться средней изобарной теплоемкостью воды в данном интервале температур.

В соответствии с выражением (6.8) процесс изобарного нагрева жидкости от t= 0 ^oС до Т_н начинается в точке 1 в T,s- диаграмме при всех давлениях и представляется логарифмической кривой 12, идущей выше линии x = 0 (см. рис. 6.11). Площадь под кривой 12 соответствует теплоте жидкости q'. При этом линии 12 и x = 0 очень близки друг к другу, что позволяет с достаточной точностью в области жидкости изобары с умеренными значениями давлений воспринимать как линию x=0 от t=0 ^oС до Т_н.

Определение энтальпии, энтропии и внутренней энергии жидкости при температурах меньших, чем температура насыщения при заданном давлении, ведется аналогичным образом.

6.4. Сухой насыщенный пар

В
фазовых диаграммах Р,v- и T,s cостояния сухого насыщенного пара определяются точками правой пограничной кривой КЛ на линии х=1 (рис. 6.12 и 6.13).

Процесс 23 фазового перехода жидкости от состояния насыщения в сухой насыщенный пар является изобарно-изотермическим, т.е. здесь изобара совпадает с изотермой насыщения воды. Рассмотрим методику определения калорических параметров сухого насыщенного пара.

Теплота, затраченная на превращение 1 кг жидкости в состоянии насыщения (кипения) в сухой насыщенный пар при постоянном давлении (температуре), называется удельной теплотой парообразования и обозначается буквой r, она может быть определена экспериментально.

Все параметры сухого насыщенного пара отмечаются двумя штрихами (v", h", s" и т.д.). Исходя из первого закона термодинамики для процесса парообразования можно записать:

r = u"- u' + Р(v"- v') = h"- h'. (6.9)

В процессе парообразования температура не изменяется, следовательно, разность внутренних энергий u" - u' соответствует только изменению потенциальной ее составляющей или, как ее называют, работе дисгрегации (разъединения молекул), т.е. собственно работе перевода жидкости в пар. Она называется внутренней теплотой парообразования и обозначается буквой :

 = u" - u' . (6.10)

Работа изменения объема при парообразовании называется внешней теплотой парообразования и обозначается буквой :

 = Р(v" - v') . (6.11)

В диаграмме Р,v она представлена площадью под горизонталью 23 (рис.6.12). Использовав введенные обозначения, уравнение (6.9) можно представить в виде

r =  +  . (6.12)

При критическом давлении все члены равенства (6.12) равны нулю: r===0.

В изобарном процессе 123 (см. рис.6.13) затрачивается теплота для нагрева жидкости от t=0 ^оС до состояния сухого насыщенного пара, называющаяся полной теплотой сухого насыщенного пара:

" = q' + r = q' +  +  = h" - Рv_o' . (6.13)

Эта теплота и все ее слагаемые зависят от давления или от температуры насыщения. Зависимость этих величин от температуры насыщения представлена на рис. 6.14.

Теплоту парообразования можно выразить через разницу энтальпий (6.9). Следовательно, энтальпию сухого насыщенного пара можно определить как

h" = h' + r = q' + Рv_o' + r = " + Рv_o'. (6.14)

Из рис. 6.14 видно, что " имеет максимум. Поскольку Рv_o' несоизмеримо мала по сравнению с ", то и h" имеет максимум. При этом важно отметить, что максимум энтальпии сухого насыщенного пара h" находится при температуре меньшей, чем у критической точки.

Внутренняя энергия сухого насыщенного пара определяется из соотношения

u" = h" - Рv" . (6.15)

Изменение энтропии при изобарно-изотермическом процессе парообразования 23 может быть определено как

, (6.16)

откуда получаем значение энтропии сухого насыщенного пара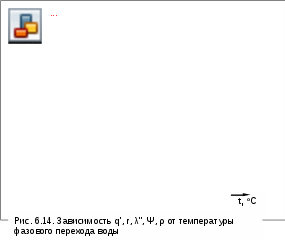



^″_max
. (6.17)

6.5. Влажный насыщенный пар

Влажный насыщенный пар располагается между пограничными кривыми x = 0 и x = 1. Возьмем точку е на изобаре Р в области влажного насыщенного пара (рис. 6.15 и 6.16). В области влажного насыщенного пара параметры состояния не могут быть определены только по давлению и температуре, поскольку давление однозначно определяет температуру насыщения и изобара влажного пара одновременно является его изотермой, представляющей прямую линию в Р,v- и Т,s- диаграммах. В качестве вспомогательного условного параметра для влажного пара применяется степень сухости х. Зная степень сухости х и параметры состояний насыщения воды на линии х=0 и пара на линии х=1, можно рассчитать все остальные параметры состояния влажного пара.

П

xr

q′
араметры влажного пара обозначаются с индексом "x". 1 кг влажного пара содержит х кг сухого насыщенного пара и (1 - x) кг воды в состоянии насыщения. Следовательно, любой параметр, подчиняющийся закону сложения (аддитивности), для 1 кг влажного пара будет представлен в виде суммы произведений соответствующих параметров на x кг сухого насыщенного пара и на (1-x) кг воды при давлении или температуре насыщения. Например, расчет удельного объема, энтальпии, энтропии и внутренней энергии для влажного пара можно выполнить по формулам

v_x = xv" + (1 - x)v' = v' + x(v" - v'); (6.18)

h_x = h' + x(h" - h') = h' + xr; (6.19)

s_x = s '+ x(s" - s'); (6.20)

u_x = u' + x(u" - u'). (6.21)

Используя параметры влажного насыщенного пара, можно рассчитать его степень сухости: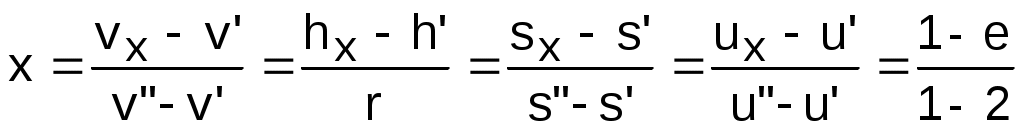

. (6.22)

При этом горизонтальные отрезки 12 изобар и изотерм в Р,v- и T,s- диаграммах в области влажного насыщенного пара делятся точкой е пропорционально значению степени сухости х=(1е)/(12), что позволяет построить линии постоянных степеней сухости х=const (см. рис. 6.15 и 6.16). В критической точке сходятся все линии постоянных степеней сухости. Внутренняя энергия влажного пара проще определяется как

u_x = h_x - Рv_x . (6.23)

Теплота, необходимая для получения влажного пара из воды c t=0 ^оС при изобарном ее нагревании, называется полной теплотой влажного пара и определяется как

_x = q' + xr = h_x - Рv_o'. (6.24)

Наряду со степенью сухости x в практике часто используется понятие влажности пара (1-x). Влажность дается в долях или в процентах.

6.6. Перегретый пар

И зобарный подвод теплоты к сухому насыщенному пару приводит к повышению его температуры по отношению к температуре насыщения при данном давлении. Параметры состояния перегретого пара обозначаются соответствующими буквами без индексов (t, h, s, u и т.д.).

Получение перегретого пара можно рассмотреть на примере энергетического парогенератора. В парогенераторах для перегрева пара используют пароперегреватели, представляющие собой трубную поверхность теплообмена (рис.6.17). Внутри труб пароперегревателя проходит пар, поступающий из котла в виде влажного пара. Поверхность труб омывается горячими продуктами сгорания топлива (на ТЭС) или горячей водой или паром большего давления (на АЭС). Не учитывая незначительного падения давления, вызванного гидравлическим сопротивлением в трубах, процесс перегрева пара в пароперегревателе можно считать изобарным.

Рассмотрим методику определения калорических параметров перегретого пара. В соответствии с первым законом термодинамики теплота при перегреве пара затрачивается на изменение его внутренней энергии и на работу изменения объема. При этом теплота, идущая на изменение внутренней энергии пара, расходуется на изменение кинетической энергии молекул, что проявляется в изменении температуры, и на преодоление сил взаимодействия между молекулами – работу дисгрегации (разделения частиц). Работа изменения объема расходуется на преодоление внешнего давления и при изобарном процессе определяется как Р(v - v").

Теплота, необходимая для перевода 1 кг сухого насыщенного пара в перегретый пар с температурой t при изобарном ее нагревании, называется теплотой перегрева q_п (рис. 6.18) и может быть определена как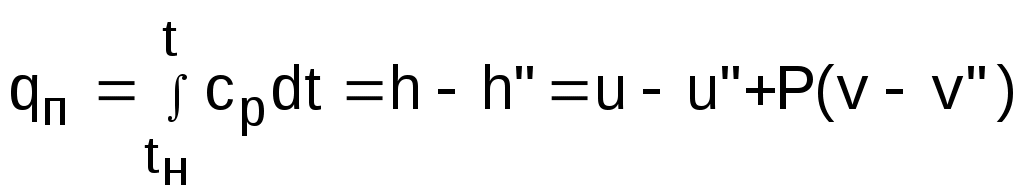

, (6.25)

где c_p – массовая изобарная теплоемкость перегретого пара.

И зобарная теплоемкость перегретого пара является переменной величиной, зависящей от давления и температуры. Она определяется экспериментально. На рис. 6.19 представлена зависимость изобарной теплоемкости перегретого пара от давления и температуры в области докритических давлений. В системе координат c_p,t изображены изобары, крайние левые точки которых, соединенные пунктирной кривой, определяют c_p при температуре насыщения, т.е. это изобарные теплоемкости сухого насыщенного пара на линии х=1.

Анализ представленных на графике опытных данных при Р<Р_кр приводит к выводу:

1) при постоянном давлении с повышением температуры от температуры насыщения изобарная теплоемкость сначала уменьшается, проходит через минимум, а затем медленно возрастает;

2) при одной и той же температуре c_p тем больше, чем выше давление;

3
) с повышением температуры зависимость c_p от Р уменьшается.

На рис. 6.20 даны экспериментальные кривые зависимости изобарной теплоемкости жидкой воды и пара при давлениях выше критического.

Анализ изменения изобарной теплоемкости воды и пара при Р>Р_кр показывает:

1) при критическом давлении с повышением температуры жидкости ее изобарная теплоемкость растет и при критической температуре переходит в бесконечность, далее вблизи критической точки при t>t_кр c_p пара резко понижается;

2) при сверхкритических давлениях повышение температуры воды сопровождается повышением c_p воды до максимума, а затем понижением теплоемкости пара;

3) с повышением давления уменьшается степень изменения c_p от температуры, значение максимума снижается, а максимум теплоемкости смещается в область более высоких температур.

П
оскольку изобарная теплоемкость перегретого пара является величиной переменной, определение энтальпии перегретого пара ведется через теплоту перегрева

h = h" + q_п , (6.26)

а энтропию перегретого пара рассчитывают, используя экспериментальные данные по зависимости теплоемкости от температуры и давления, по формуле

. (6.27)

Проведенный анализ определения термодинамических свойств воды и водяного пара приводит к выводу, что нахождение параметров воды и пара связано с трудоемкими экспериментальными исследованиями и сложными математическими вычислениями. Поэтому экспериментальные данные и расчеты, выполненные на их основе, по определению калорических параметров и других характеристик воды и водяного пара используются для составления таблиц термодинамических свойств воды и водяного пара и для построения диаграмм. C применением данных этих таблиц выполняются все расчеты, в которых необходимы параметры и характеристики воды и водяного пара.

6.7. Таблицы термодинамических свойств воды и водяного пара

Инженерные расчеты процессов изменения состояния воды и водяного пара и паровых циклов осуществляются по таблицам термодинамических свойств воды и водяного пара [11]. Эти таблицы составлены на основании надежных экспериментальных данных с согласованием результатов экспериментов и расчетных величин на межгосударственных уровнях.

В нашей стране утвержденным стандартом являются таблицы термодинамических свойств воды и водяного пара, составленные М.П.Вукаловичем, С.Л.Ривкиным, А.А.Александровым [11]. Они включают в себя данные по термодинамическим свойствам воды и водяного пара в диапазоне изменений давления от 0,0061 до 1000 бар и температуры от 0 до 1000 ^оС.

Таблицы содержат все данные, необходимые для расчетов термодинамических параметров в области жидкости, влажного пара и в области перегретого пара. В таблицах не приведены значения внутренней энергии, для ее расчета используется соотношение u = h - Рv. При расчете внутренней энергии необходимо обратить внимание на соответствие единиц измерения энтальпии h, она в таблицах приведена в килоджоулях на килограмм (кДж/кг), и произведения pv, при использовании давления в килопаскалях (кПа) это произведение тоже будет в килоджоулях на килограмм (кДж/кг).

Таблицы построены следующим образом. Первая и вторая таблицы описывают свойства воды и водяного пара в состоянии насыщения как функции от температуры (1-я таблица) и давления (2-я таблица). Эти две таблицы дают зависимость параметров на линиях x = 0 (вода в состоянии насыщения) и x = 1 (сухой насыщенный пар) от температуры и давления. Нахождение всех параметров ведется по одной величине; в табл. 1 – по температуре, в табл. 2 – по давлению насыщения. Эти определяющие параметры находятся в крайних левых столбцах таблиц. Далее в правых столбцах идут соответствующие Р_н и t_н величины: v' и v", h' и h", r=h"-h', s' и s", s"-s'. Параметры с одним штрихом относятся к воде в состоянии насыщения, с двумя штрихами – к сухому насыщенному пару. Величины параметров влажного насыщенного пара определяются расчетным путем с использованием степени сухости x. Для облегчения этих расчетов в таблицах даны величины r и s"-s'. Например, определение удельного объема, энтальпии и энтропии влажного пара ведется по формулам

v_х = v' + x(v" - v') ;

h_x = h' + xr;

s_x = s' + x(s" - s').

Диапазон определяющих параметров этих таблиц: от t=0 ^oС до t_кр=374,12 ^oС и от Р=0,0061 бар до Р_кр=221,15 бар, т.е. нижний предел – тройная точка воды, верхний предел – критическая точка воды.

Необходимо отметить, что в качестве определяющего параметра в табл. 1 и 2 можно использовать любой из параметров (v', v", h', h", s', s"), а не только давление и температуру насыщения. Поскольку в инженерной практике Р и t выступают чаще всего в качестве определяющих параметров, их и поместили в левой колонке.

Следующая – третья – таблица описывает свойства воды и перегретого пара. Их диапазон от 0 до 1000 ^oС (может быть и до 800 ^oС) и от 1 кПа до 100 МПа. В качестве определяющих параметров здесь необходимы две величины. В 3-х таблицах – это давление – верхняя горизонтальная строка – и температура – левая крайняя колонка. Под строкой давлений дается прямоугольник, в котором приведены все параметры состояния насыщения, соответствующие данному давлению. Это позволяет быстро ориентироваться в фазовом состоянии воды и пара и, не листая таблицы, выполнять необходимые расчеты для различных фазовых состояний воды. Каждому давлению и температуре в 3-х таблицах даны v, h, s в соответствующих вертикальных колонках.

Для наглядной ориентации параметры жидкой фазы и паровой отделены в этих колонках жирными горизонтальными линиями. Выше этих линий находится жидкая фаза воды, ниже – перегретый пар. При давлениях выше критического (22,12 МПа) эти разделительные линии отсутствуют, т.к. при сверхкритических параметрах нет линии видимого фазового перехода жидкости в пар.

В табл. 3 в качестве определяющих, кроме Р и t, может выступать любая пара параметров: Р, t, v, h, s.

При ориентации в фазовых состояниях воды и пара с использованием таблиц необходимо помнить:

1) при Р = const:

t < t_н – жидкая фаза воды,

t > t_н – перегретый пар,

t = t_н – необходим 3-й параметр,

например:

h = h'- кипящая вода,

h = h" – сухой насыщенный пар,

h' < h < h" – влажный пар,

h < h' – жидкая фаза воды,

h > h" – перегретый пар,

h' < h < h" – влажный пар.

2) при t = const:

Р < Р_н – перегретый пар,

Р > Р_н – жидкая фаза воды,

Р = Р_н – аналогично t = t_н при Р=const с ориентацией на h, v, s.

Некоторыение выпуски таблиц включают в себя 2 части: 1-я в СИ, где Р – в Па, h – в кДж/кг, и 2-я в СГС, где Р – в кгс/см², а h – в ккал/кг.
6.8. Диаграмма T,s для воды и водяного пара
Для иллюстрации процессов изменения состояния воды и водяного пара и паровых циклов широко используется T,s- диаграмма. Она дает большой объем информации, позволяющий судить об особенностях энергетических эффектов и о тепловой экономичности циклов.

В
тепловой диаграмме T,s наносятся линии постоянных параметров воды и пара и функций состояния (рис. 6.21).

Нулевое значение энтропии соответствует тройной точке жидкости (0,01 ^оС или 273,16 К и 611,2 Па). Построение линий постоянных параметров и функций состояния проводится по данным таблиц термодинамических свойств воды и водяного пара. Используя табличные значения зависимости между температурой насыщения Т_н и энтропией кипящей жидкости s' и сухого насыщенного пара s", можно построить нижнюю (х=0) и верхнюю (х=1) пограничные кривые. Эти пограничные кривые соединяются в критической точке К с координатами Т_кр=647,27 К (374,12 ^оС) и s_кр = 4,4237 кДж/(кг·К). Линия х = 0 начинается в тройной точке жидкости при Т = 273,16 К и s₁' = 0. Сухому насыщенному пару в тройной точке соответствует энтропия s_N"=9,1562 кДж/(кг·К) (см. рис. 6.21, точка N). Ниже горизонтали 1N находится зона сублимации, здесь слева от линии х = 1 – область твердой фазы и пара, а справа от линии х = 1 – область перегретого пара. Выше линии х = 0 находится область жидкой фазы, а выше линии х=1 находится область перегретого пара. Видимой зоны перехода от области жидкой фазы к области пара при сверхкритических параметрах нет, условно этот переход можно брать по критическим параметрам Т_кр, Р_кр или v_кр, считая область выше критической точки и правее Р_кр или v_кр областью пара.

Изобара докритического давления в T,s- диаграмме представляет собой сложную кривую 1234. Она состоит из трех частей: 12 – в области жидкости, 23 – в области влажного насыщенного пара, 34 – в области перегретого пара. Конфигурация изобары может быть установлена при использовании углового коэффициента из выражения

q_p = (c_pdT)_p = (Tds)_p ,

откуда угловой коэффициент будет равен

. (6.28)

Исходя из выражения углового коэффициента (6.28), который определяет угол наклона касательной к изобаре, следует, что в области жидкости и в области перегретого пара при подводе теплоты значения Т/c_p и s возрастают, угол наклона касательной увеличивается, т.е. здесь изобара представляет собой вогнутую кривую. Причем в области жидкости при небольших давлениях c_p – величина, мало изменяющаяся в зависимости от температуры, и изобара представляет собой логарифмическую кривую. В области перегретого пара c_p сильно зависит от температуры и изобара представляет собой логарифмическую кривую с переменной логарифмикой (о характере изменения c_p в области перегретого пара было написано ранее). В области влажного насыщенного пара изобара совпадает с изотермой, c_p=, и в T,s- диаграмме она представляет горизонтальную прямую 23.

При небольших давлениях (до 100 бар) изобары жидкости очень близки к нижней пограничной кривой (х = 0). Поэтому при использовании T,s- диаграммы для иллюстраций процессов воды и пара часто считают, что изобары жидкости совпадают с линией х=0.

Площадь под изобарой 12 (нагрев жидкости) соответствует теплоте жидкости q', под изобарой 23 (парообразование) – теплоте парообразования r, под 34 (перегрев пара) – теплоте перегрева q_п. Площадь под процессом 2e соответствует теплоте, расходуемой на испарение x-й доли из 1 кг насыщенной жидкости.

Для любого состояния в области влажного насыщенного пара (точка е) степень сухости может быть определена графически в виде отношения двух отрезков изобары между пограничными кривыми х=0 и х=1: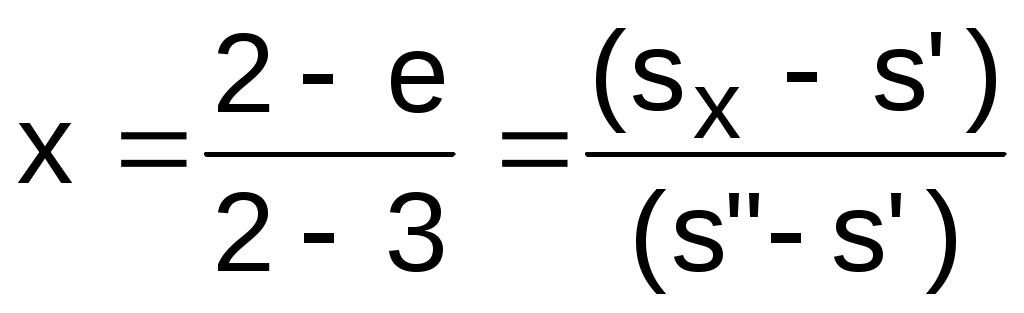

.

По этому принципу можно построить линии постоянных степеней сухости х=const.

Изобара критического давления в критической точке К имеет перегиб, здесь касательная к ней есть горизонтальная прямая. Изобары сверхкритического давления не попадают в область влажного пара и представляют собой непрерывно повышающиеся кривые с точками перегиба, в которых касательные имеют минимальный наклон. Этим точкам соответствуют максимальные значения изобарной теплоемкости.

Изохоры с v < v_кр пересекают только нижнюю пограничную кривую х=0 и размещаются в области жидкости при высоких давлениях и температурах, а в области влажного насыщенного пара – при низких давлениях и температурах.

Для всех изохор, соответствующих удельному объему больше удельного объема жидкости в тройной точке воды, с понижением давления и температуры влажного пара его степень сухости стремится к нулю, но никогда его не достигнет, поэтому изохоры никогда не достигают нижней пограничной кривой (за исключением аномальной области в интервале температур 0 - 8 ^оС).

Изохоры с v > v_кр в области перегретого пара представляют собой вогнутые кривые (круче изобар), а в области влажного пара - кривые двоякой кривизны: выпуклые - при больших степенях сухости и вогнутые - при малых степенях сухости. При этом они пересекают только правую пограничную кривую х = 1.

На рис. 6.21 показаны линии постоянных энтальпий h=const. В области перегретого пара изоэнтальпа представляет собой плавную кривую с отрицательным тангенсом угла наклона к ней. Изоэнтальпы, переходящие из области влажного пара в область жидкости, имеют ярко выраженную точку излома на линии х = 0. В области жидкости наклон изоэнтальпы изменяется так, что при малых значениях энтальпий с повышением давления температура понижается, а при больших значениях энтальпий повышение давления сопровождается и повышением температуры.

На рис. 6.21 в точках 2 и 3 проведены касательные к пограничным кривым х=0 и х=1. Подкасательные c' и c" представляют собой теплоемкости жидкости и сухого насыщенного пара на пограничных кривых (при изменении состояния по х=0 и х=1). Оказывается, что c'>0, а c"<0. Последнее означает, что при понижении температуры для поддержания пара в состоянии сухого насыщенного к нему необходимо подводить теплоту.

6.9. Диаграмма h,s для воды и водяного пара

В инженерной практике широкое применение находит h,s- диаграмма для воды и водяного пара. Такое широкое использование h,s- диаграммы в теплоэнергетических расчетах обусловлено тем, что для основных процессов теплоэнергетических установок (изобарного, Р=const, и адиабатного, s=const) разности энтальпий представляют их главные энергетические характеристики: количество теплоты или техническую работу, которые в h,s- диаграмме могут быть элементарно представлены отрезками вертикальных прямых линий. В Т,s- диаграмме эти величины представляются сложными площадями.

Диаграмма h,s строится по данным таблиц термодинамических свойств воды и водяного пара. На рис. 6.22 приведен общий вид такой диаграммы для воды и водяного пара.

За начало отсчета энтропии в h,s- диаграмме, как и в Т,s- диаграмме, приняты параметры тройной точки жидкой фазы воды. В этой точке s_о'=0 и u_о'=0, а энтальпия h_о' = 0,000614 кДж/кг будет больше нуля, но численное ее значение очень мало. Следовательно, начало линии х=0, соответствующее тройной точке воды, расположено очень близко к началу координат. При повышении давления и температуры энтальпия h' и энтропия s' жидкости на линии насыщения растут до критической точки и пограничная линия х=0 представляется вогнутой кривой ОК.

Пограничная кривая сухого насыщенного пара х=1 имеет вид кривой КN. Максимальное значение энтальпии (ординаты) этой кривой h"_мах=2801,9 кДж/кг достигается при давлении около 30 бар и энтропии 6,18 кДж/(кг·К). Следует обратить внимание на то, что критическая точка находится левее и ниже точки максимальной энтальпии h"_мах, а вся пограничная кривая х=1 располагается выше горизонтали, проведенной из критической точки.

И
зотерма 0 ^oС в области жидкости имеет сложную форму ОВ, определяемую аномалией воды. Максимум энтропии линии ОВ около 0,9 Дж/(кг·К) при давлении около 240 бар и энтальпии 24 кДж/кг. При давлениях выше 240 бар нулевая изотерма уходит влево и при 1000 бар достигает значения h_o'=95,9 кДж/кг и s_о'=-6,7 Дж/(кг·К).

Изобара в h,s- диаграмме представляет собой непрерывно поднимающуюся линию, форма которой устанавливается соотношением

q_p = dh_p = (Tds)_p ,

откуда получается угловой коэффициент изобары

. (6.29)

Таким образом, он определяется абсолютной температурой. Следовательно, изобары жидкости представляют собой вогнутые кривые, идущие слева направо, поскольку процесс нагрева жидкости 12 сопровождается возрастанием энтропии и повышением температуры.

В процессе изобарного парообразования 23 температура остается постоянной, и участок изобары 23 представляет прямую, угол наклона которой определяется температурой насыщения Т_н. На пограничных кривых (х=0 и х=1) вода имеет одну и ту же температуру, следовательно, прямая 2-3 является касательной к кривым 12 и 34.

С повышением давления увеличивается температура насыщения, и, как следует из (6.29), в области влажного пара изобары – изотермы веерообразно расходятся.

Изобара парообразования 23 плавно переходит в изобару перегретого пара 34, представляя собой вогнутые расходящиеся кривые, при большой степени перегрева приближающиеся к эквидистантным кривым логарифмического характера (как для газов).

Критическая изобара проходит через критическую точку К и представляет собой вогнутую кривую. Изобары сверхкритического давления имеют такой же вид. Изобара наивысшего давления ограничивает поле диаграммы. Для точек, расположенных левее этой изобары, табличных данных нет. Такую же роль ограничивающей линии снизу в области перегретого пара и в области влажного пара выполняет изобара с давлением 1 кПа.

В области жидкости изобары докритических давлений мало отступают от линии х=0. Поэтому их часто считают совпадающими с нижней пограничной кривой.

Изотермы в h,s- диаграмме представляют собой сложные линии. Изотермы жидкости при низких температурах, начиная от 0 ^оС, с повышением давления поднимаются вверх (кривые выпуклостью вверх); при высоких температурах – кривая выпуклостью вниз.

В области влажного пара изотермы совпадают с изобарами. В области перегретого пара изотермы имеют вид кривых выпуклостью вверх, идущих слева направо. При низких температурах кривизна и подъем незначительны. При температурах, близких к критической, в области высоких давлений изотермы перегретого пара круто идут вверх, имея большую кривизну. В областях низких давлений все изотермы перегретого пара приближаются к горизонтальным прямым (свойства пара близки к свойствам идеальномого газа).

Изотерма наивысшей, имеющейся в таблицах температуры рассматривается как линия, ограничивающая диаграмму сверху. Для состояний выше этой изотермы табличных данных нет.

Изохоры в h,s- диаграмме представляют собой плавные кривые, круче изобар. Они могут пересекать только одну пограничную кривую (х=0 или х=1), в зависимости от того, удельный объем их меньше или больше удельного объема воды в критической точке.

На рис. 6.22 выделена изобара 1234 и показаны в виде отрезков значения энтальпии, энтропии и их разности для характерных состояний воды и пара на этой изобаре. Точке 1 соответствует состояние жидкости при t=0 ^оС и данном давлении. На рис. 6.22 область жидкости увеличена по масштабу по сравнению с областями пара, это сделано для большей наглядности в изображении линий. Так при Р = 100 бар и t=0 ^оС в точке 1 энтальпия воды h₀ = 10,1 кДж/кг (для сравнения, при том же давлении h' = 417,5 кДж/кг и h"= 2675,7 кДж/кг). Точкой е отмечено состояние влажного пара со степенью сухости х. Линия x = const строится из соотношения

.

Для практических расчетов используется не полная диаграмма h,s, а только ее рабочая зона в области пара, наиболее часто применяемая в инженерной практике. Она располагается правее критической точки, включая в себя области влажного пара и перегретого пара (рис. 6.23). Левая область не изображается, так как в ней линии изобар, изотерм, изохор и постоянные степени сухости располагаются очень близко друг от друга и неудобны в практическом использовании.

Применяя рабочую диаграмму h,s, можно получить полную информацию о паре, состояние которого задано точкой. Так, например, на рис. 6.23 в диаграмме h,s задана точка 1, определяющая состояние влажного насыщенного пара. Положение точки задается двумя параметрами, например давлением Р₁ и степенью сухости x₁. По осям координат читаются значения энтальпии h₁ и энтропии s₁. Через точку 1 проходит изохора, определяющая удельный объем пара v₁. Температура t₁ определяется по изотерме, проходящей через точку 1 и ответвляющейся от изобары P₁ на пограничной кривой x = 1 в области перегретого пара. Аналогично находятся параметры состояния пара, заданного любой точкой (парой параметров) в диаграмме h,s. Параметры точек, выходящих за пределы области рабочей h,s- диаграммы водяного пара, находятся по таблицам термодинамических свойств воды и
водяного пара.
6.10. Основные процессы изменения состояния водяного пара

Для расчета процессов изменения состояния водяного пара не используются имеющиеся для него уравнения состояния, ввиду их сложности и ограничений применимости в зависимости от области параметров состояния водяного пара (в различных областях используются различные уравнения). Применение таких уравнений оправдано, когда они заложены в современные ЭВМ и машина сама считает параметры по любой известной паре параметров по специальной программе.

Практически расчет процессов изменения состояния воды и водяного пара осуществляется с использованием таблиц их термодинамических свойств и диаграмм. Из диаграмм наибольшее применение нашли h,s- диаграммы.

Наиболее простым и наглядным является метод расчета паровых процессов с использованием h,s- диаграммы. Здесь не нужно выяснять, в какой области протекает процесс, есть ли переход из зоны перегретого пара в зону влажного пара или наоборот. Все это видно по графику процесса. Расчет сводится к чтению диаграммы и при необходимости к подсчету по полученным из диаграммы данным работы, теплоты и изменений параметров и функций состояния. Когда процесс выходит за пределы рабочей h,s- диаграммы, расчет проводится с использованием таблиц термодинамических свойств воды и водяного пара.

Диаграммы Р,v и T,s служат для иллюстрации особенностей процессов и могут быть применены для графического изображения в виде площадей энергетических величин q, , u , характеризующих данный процесс.

В практике теплоэнергетики наиболее часто встречаются: изохорный процесс (растопка котла при повышении давления), изобарный процесс (установившийся режим работы котла, процессы в подогревателях и конденсаторах пара), адиабатный процесс (в паровой турбине и насосе), изотермический процесс (испарение воды в реакторе кипящего типа).

Рассмотрим подробно эти процессы, считая их обратимыми.