пособие. ТТД ч1 учебное пособие. Техническая термодинамика
 Скачать 4.15 Mb. Скачать 4.15 Mb.
|
|
4.5. Качественный и количественный анализ политропных процессов в Р,v- и T,s- диаграммах При протекании любого газового процесса происходит энергообмен газа с внешней средой и изменение его параметров. Имея изображение политропного процесса в Р,v- и T,s- диаграммах, всегда можно определить знак теплоты, работы и знак изменения параметров этого процесса, т.е. провести качественный анализ процесса. Для иллюстрации этого на рис. 4.11 и 4.12 через произвольную точку А, определяющую начало процесса в Р,v- и T,s- диаграммах, проведены основные термодинамические процессы: изобара, изохора, изотерма, адиабата. Во всех процессах, начинающихся в точке А и располагающихся справа от изохоры (n = ), объем увеличивается (dv>0), и, следовательно, работа имеет положительный знак (l=Pdv>0). В процессах, заканчивающихся слева от изохоры, знаки dv и l отрицательные. В процессах, располагающихся справа от адиабаты (n=к), энтропия возрастает (ds>0), и теплота имеет положительный знак (q=Tds>0), т.е. теплота к газу подводится. В процессах, заканчивающихся с левой стороны от адиабаты, знаки ds и q отрицательные. В 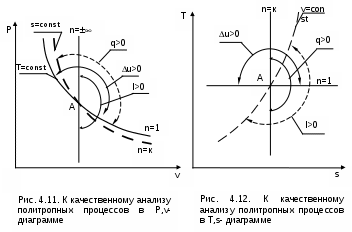 процессах, заканчивающихся выше изотермы (n=1), температура возрастает (dT>0), и увеличивается внутренняя энергия и энтальпия газа (du=cvdT>0, dh=cpdT>0). В процессах с противоположной стороны от изотермы величины dT, du и dh отрицательные. Поскольку площадь под процессом в P,v- диаграмме есть работа изменения объема, а в T,s- диаграмме – теплота, то, имея изображение процесса в этих координатах, можно дать и количественную характеристику процесса. Например, на рис.4.13 изображен политропный процесс идеального газа 12 в Р,v- диаграмме. Площадь под процессом 122'1'1 есть работа изменения объема l. Изменению внутренней энергии процесса 12 соответствует работа любого адиабатного процесса в пределах температур от T1 до T2, т.е. u=u2-u1=ls=сv(T2- T1)=пл.2аа'2'2. (а) Проведя адиабату через точку 2 и найдя точку пересечения с ней изотермы T1=const, получим процесс 2а, площадь под которым есть изменение внутренней энергии u2-u1. Сумма двух заштрихованных площадей представляет теплоту процесса q = u2 - u1 + l = пл.12аа'1'1. (б) Выражение первого закона термодинамики с использованием энтальпии, 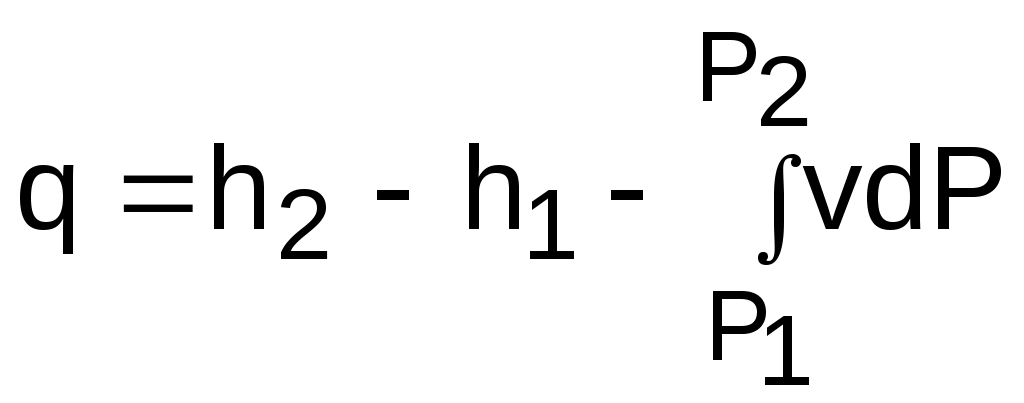 , (в) , (в)позволяет графически представить его составляющие в Р,v- координатах. Величине – 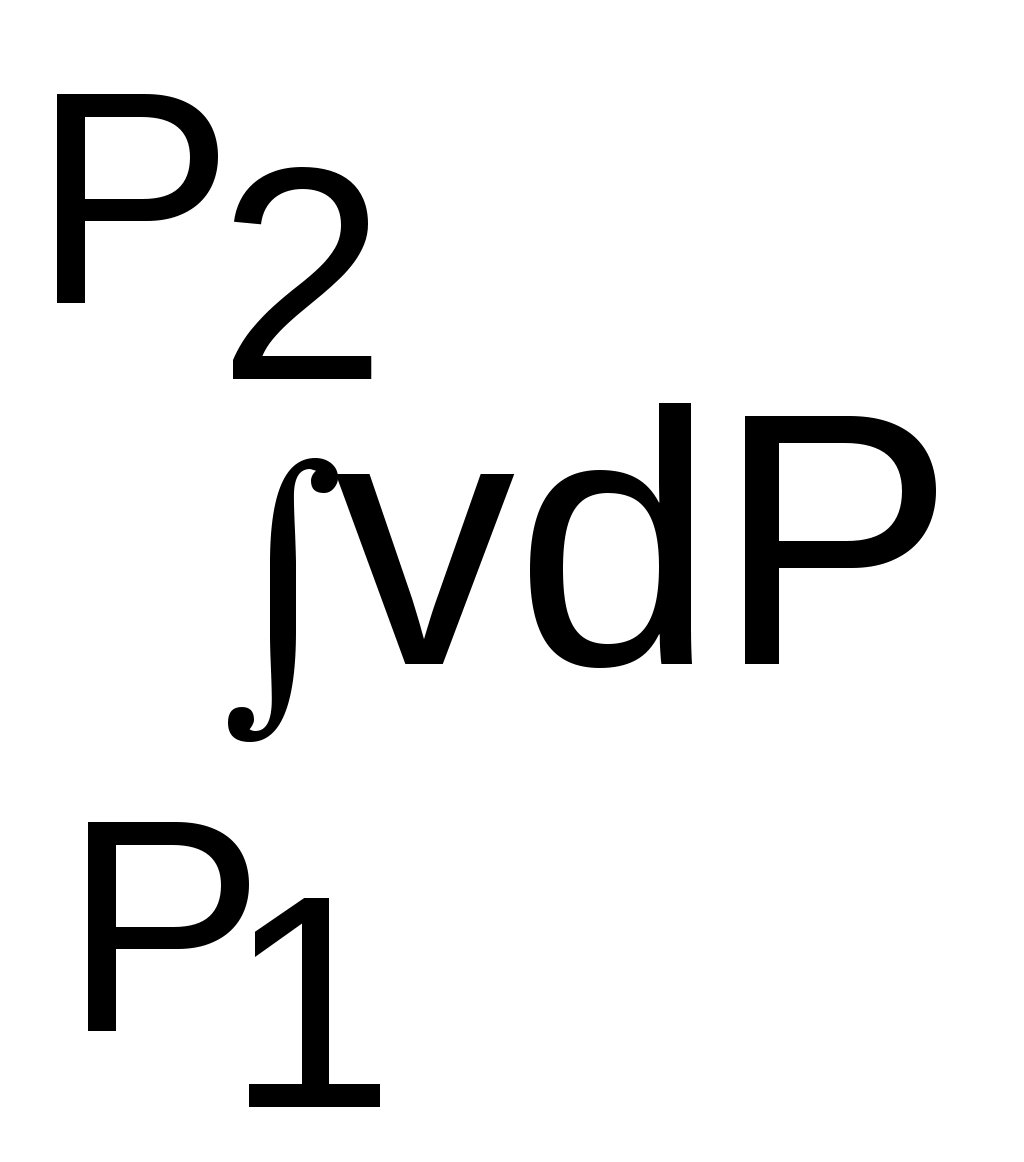 в Р,v- диаграмме соответствует площадь под процессом 12 в проекции на ось давлений 122"1"1. в Р,v- диаграмме соответствует площадь под процессом 12 в проекции на ось давлений 122"1"1.Р 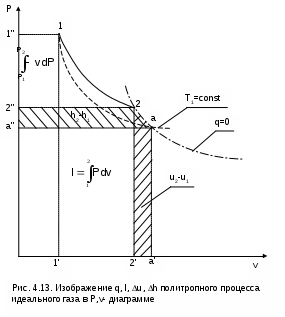 азницу энтальпий можно представить в виде площади под адиабатным процессом 2а (q = 0) в проекции на ось Р в интервале температур T1 и T2: 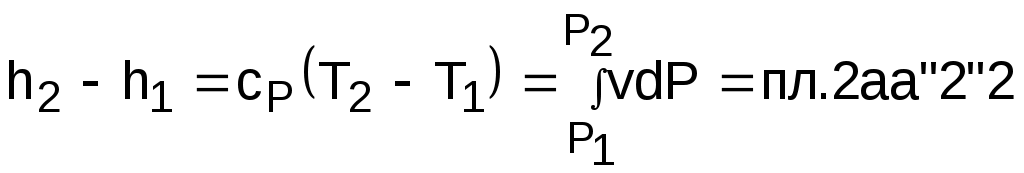 . (г) . (г)Сумма этих площадей есть теплота процесса q = пл.12aa"1"1. В T,s- диаграмме площадь под процессом 1-2 (рис. 4.14) представляет теплоту этого процесса q=пл.122'1'1. Эту площадь, согласно первому закону термодинамики, можно представить в виде двух частей: изменения внутренней энергии – площадь под любой изохорой в интервале температур Т1 и Т2: u2 - u1 = qv = cv(Т2 - Т1) = пл.22'а'а2 ; (д) и работы изменения объема, представляющей разность теплоты и изменения внутренней энергии процесса 12: l = q - (u2 - u1) = пл.12аа'1'1. (е) Изменение энтальпии в процессе 12 можно представить в виде площади под любой изобарой в интервале температур Т1 и Т2: h 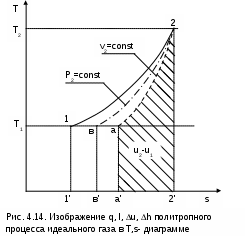 2 - h1 = qp = сp(Т2 - Т1) = пл.2вв'2'2. (ж) Таким образом, имея изображение политропного процесса газа в Р,v- или T,s- диаграмме, можно оценить величину и знак теплоты, работы изменения объема, изменения внутренней энергии, энтальпии и других термодинамических параметров состояния. 4.6. Определение термодинамических свойств идеальных газов с учетом влияния температуры на их изобарную и изохорную теплоемкости Как известно[9, 12], теплоемкость реальных газов зависит от температуры и давления. Причем зависимость теплоемкости от давления проявляется в большей степени для состояний газов и паров, близких к области насыщения (см. гл. 6). Для газов и паров, состояния которых далеки от области насыщения, зависимость cp и cv от давления незначительна и при практических расчетах ею пренебрегают. Зависимость cp и cv от температуры столь существенна, что ею при точных расчетах пренебрегать нельзя. Изменение cp и cv при изменении температуры объясняет квантовая теория теплоемкости. В отличие от кинетической теории газов квантовая теория позволяет учесть колебательное движение атомов внутри молекул двух - и многоатомных газов. Квантовая теория теплоемкости разработана Энштейном. В соответствии с этой теорией мольная изохорная теплоемкость газа представляет следующую функциональную зависимость: где h=6,6237710-27 эрг/с – постоянная Планка; k = R/N = 1,38710-16 эрг/К – постоянная Больцмана; – частота колебания атомов в молекуле; Т – абсолютная температура. Уравнения изохорной и изобарной теплоемкостей идеальных газов с учетом влияния температуры на их значения имеют весьма сложный вид и включают в себя ряд физических констант, которые могут быть определены только экспериментально. На базе последних достижений в физике в области определения точных значений фундаментальных физических констант по спектроскопическим данным были вычислены теплоемкости многих газов (cp и cv) в зависимости от температуры. Данные теплоемкости занимают промежуточное положение между теплоемкостями идеальных и реальных газов, поскольку они рассчитаны на базе квантовой теории теплоемкостей идеальных газов с привлечением экспериментальных данных по константам, входящим в расчетные уравнения этих теплоемкостей. Область практического применения этих теплоемкостей ограничена. Однако для газов и их смесей, широко используемых в практике (воздух, азот, кислород, водород, окись и двуокись углерода, гелий, продукты сгорания органического топлива и т.п.) в большом диапазоне температур и давлений справедливо уравнение Pv=RT, следовательно, в расчетах процессов этих газов можно использовать значения теплоемкостей идеальных газов cp и cv, рассчитанных по квантовой теории теплоемкостей. В свою очередь, используя значения этих теплоемкостей, можно рассчитать энергетические параметры газов. Так в литературе [12] значения теплоемкостей и производных от них энергетических параметров, приведенные в таблицах, дают погрешность не более 0,5 % по сравнению с экспериментальными значениями тех же величин для давлений до 3 МПа и температур от -50 до +1500 оС. Такой диапазон изменения параметров позволяет рассчитать большинство газовых процессов, проходящих в промышленном и энергетическом оборудовании. Определение энергетических параметров идеальных газов с учетом влияния температуры на cp и cv Рассчитанные по квантовой теории значения теплоемкостей идеальных газов cp и cv для различных температур позволяют аппроксимировать их зависимость от температуры в степенной полином вида cp = a + b1t + b2t2 + ... + bntn. (4.33) Таким образом, мы имеем функциональные зависимости cp=F1(t) и cv=F2(t). В принципе достаточно знать функциональную зависимость cp или cv от температуры, поскольку для идеальных газов cp = cv + R. На практике для удобства расчетов в справочных таблицах приводят обе теплоемкости как функции от температуры. Зная зависимости cp и cv от температуры, можно рассчитать энергетические параметры идеальных газов u, h, s, используя уравнение состояния идеального газа и первый закон термодинамики. В таблицах термодинамических свойств газов [8] расчет энергетических параметров совмещен с расчетом обратимого адиабатного процесса. Такое совмещение имеет определенную целесообразность, т.к. адиабатный процесс имеет широкое распространение в практике (в компрессорах, газовых турбинах, двигателях внутреннего сгорания и т.п.), кроме того, этот процесс довольно громоздкий в своей расчетной части. Расчет других процессов идеальных газов также может осуществляться по этим таблицам, но в этом случае определение всех энергетических параметров ведется только по температурам. Рассмотрим принцип построения таких таблиц и их использование для расчета газовых процессов. В основу построения этих таблиц положены уравнения первого закона термодинамики для обратимого адиабатного процесса идеального газа: δq = du + δl = cvdT + Pdv = 0; δq = dh - vdP = cpdT - vdP = 0. Поделив эти уравнения на уравнение состояния идеального газа Pv=RT, получим соотношения Зафиксировав начало адиабатного процесса в виде точки с постоянными параметрами Ро, Tо, vо, проинтегрируем эти выражения от точки на адиабатном процессе с температурой То до точки с температурой Т и соответствующими ей давлением и объемом Р и v (рис.4.15). В результате интегрирования получим выражения 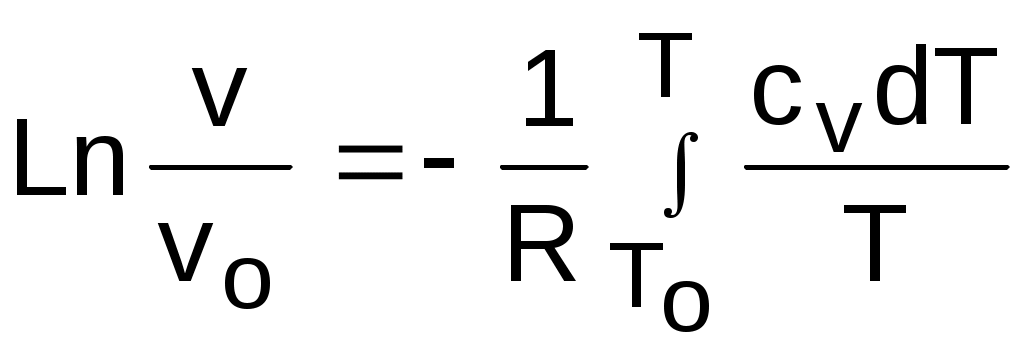 ; (4.36) ; (4.36)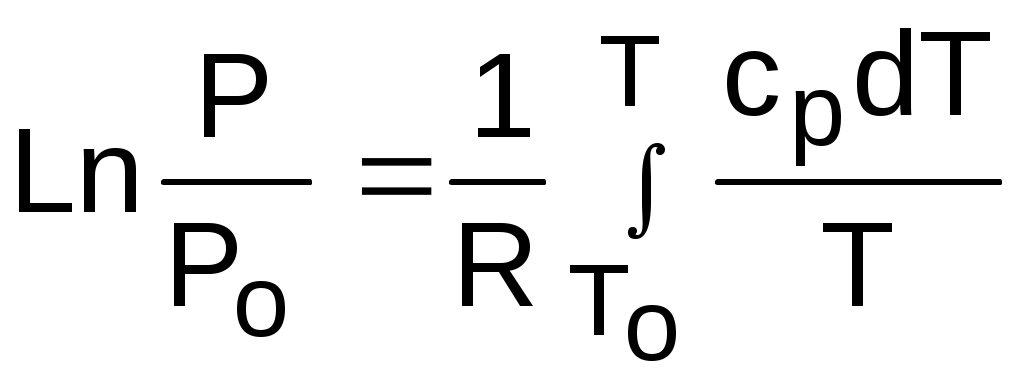 . (4.37) . (4.37)Введем понятия относительного объема o и относительного давления o: Для адиабатного процесса 12 (рис.4.16) с параметрами в начальной точке Р1, T1 и v1 и в конечной точке Р2, T2 и v2 относительные объемы и давления будут рассчитываться в соответствии с уравнениями (4.35) и (4.36) по формулам 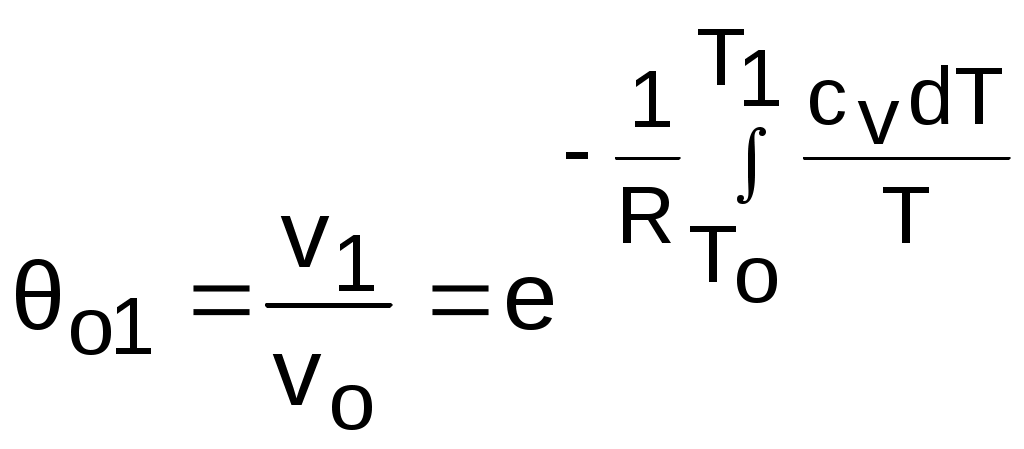 ; ; 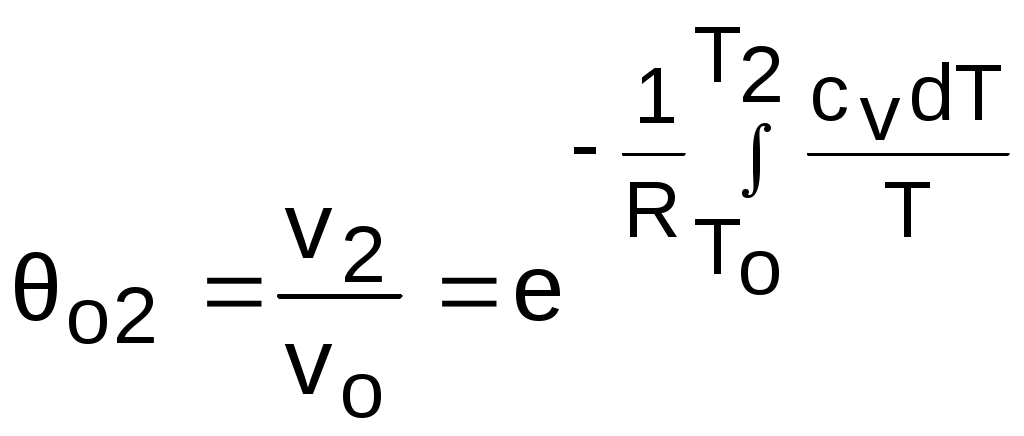 ; ;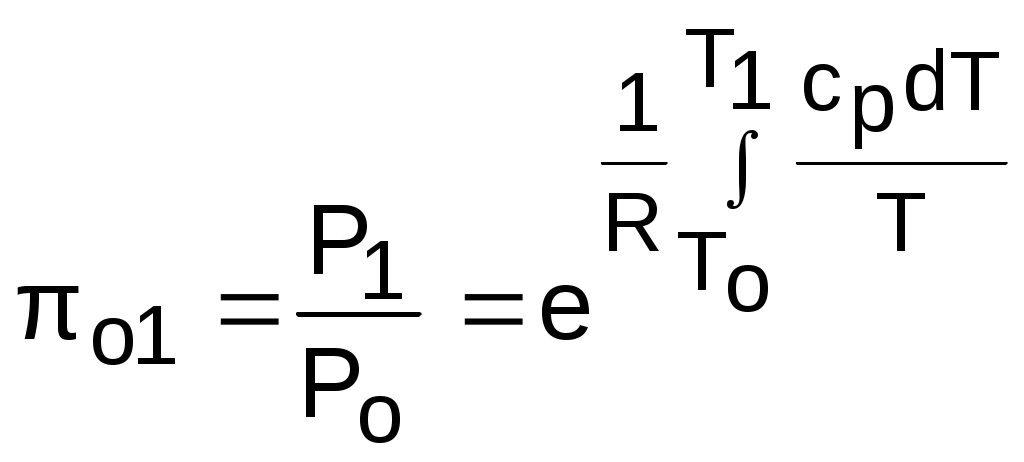 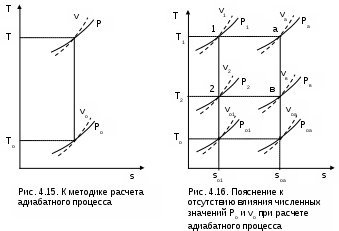 ; 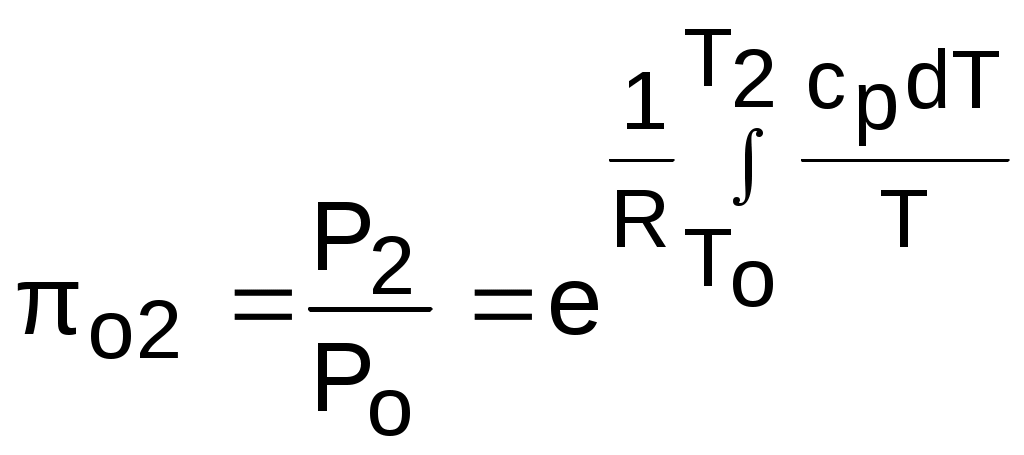 . .Из этих формул следует, что для адиабатного процесса справедливы соотношения Величины относительных объемов и давлений есть функции одного параметра – температуры, поскольку То мы приняли в виде постоянной величины, а сp и сv являются функциями температуры. При этом численные значения величин Рo и vо никакой роли не играют, поскольку в расчетах адиабатного процесса нас интересуют относительные давления и объемы, а они зависят только от То и Т. Для наглядности этого утверждения на рис.4.16 показаны два адиабатных процесса, проходящих в одном и том же интервале температур Т1 – Т2. Приняв для этих адиабат одинаковую температуру То, можно записать следующие соотношения: Из этих соотношений видно, что несоответствие энтропии so1 адиабатного процесса 12 с энтропией soа процесса ав, т.е. различие в численных значениях давлений и объемов в этих процессах при То, не влияет на отношение давлений и объемов в этих процессах, и если они проходят в одинаковых интервалах температур, то и отношения давлений и объемов будут одинаковы. Это объясняется тем, что все изобары и изохоры идеальных газов в Т,s- диаграмме – эквидистантные кривые. Характер изобары в Т,s- диаграмме определяет теплоемкость сp, а изохоры – сv, и при одинаковых температурах на всех изобарах и изохорах одинаковые теплоемкости. Таким образом, для адиабатного процесса по o1 и o1 всегда можно определить соответствующую им температуру Т1 и теплоемкости сp1 и сv1. В свою очередь, зная параметры начальной точки этого процесса и степень повышения давления р2/р1 или степень сжатия v1/v2, можно определить параметры конца процесса, найдя 02=01(p2/p1) или 02=01(v2/v1), а по ним определить температуру Т2 и рассчитать весь адиабатный процесс. В таблицах [12] в качестве То для расчета o и o принято значение температуры абсолютного нуля. В принципе можно брать любое То, а Ро и vо вообще роли не играют (см. приведенный выше анализ). Для определения внутренней энергии и энтальпии газов принимают начало отсчета внутренней энергии uo=0 при Тo. В качестве То в таблицах [8] принят абсолютный нуль, То=0 К. Расчет u и h ведется по формулам идеальных газов: 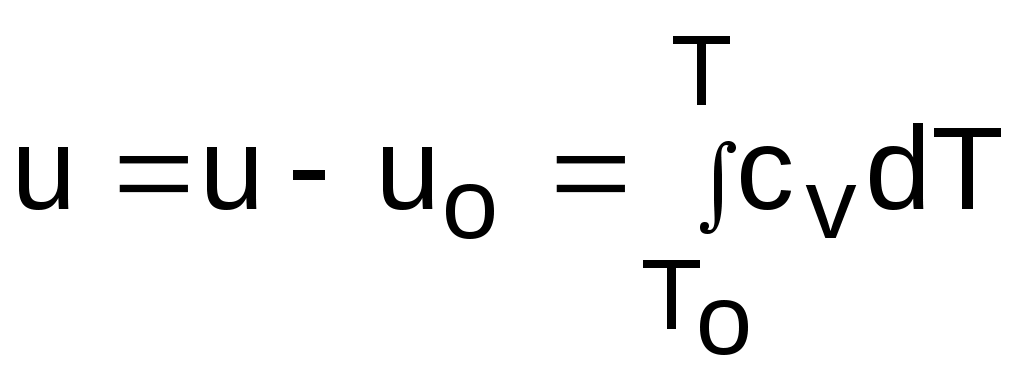 ; (4.42) ; (4.42)При этом в нашем случае начала отсчета внутренней энергии и энтальпии совпадают и равны нулю, т.к. То= 0 К. Энтальпия может быть рассчитана аналогично внутренней энергии интегрированием, при этом используется функциональная зависимость теплоемкости сp от температуры: 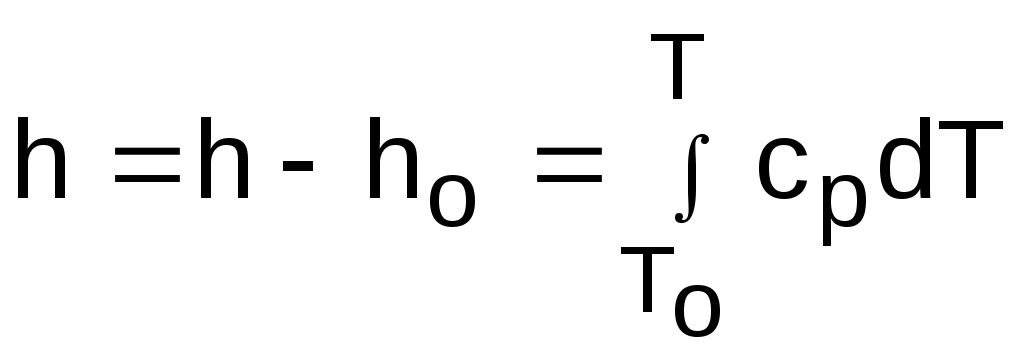 . (4.44) . (4.44)Поскольку u и h являются функциями температуры, они могут быть определены и через o и o. Для расчета изменения энтропии используется первый закон термодинамики для обратимых процессов идеальных газов: Интегрируя это выражение для двух состояний идеального газа, получим формулу для расчета разности энтропий: 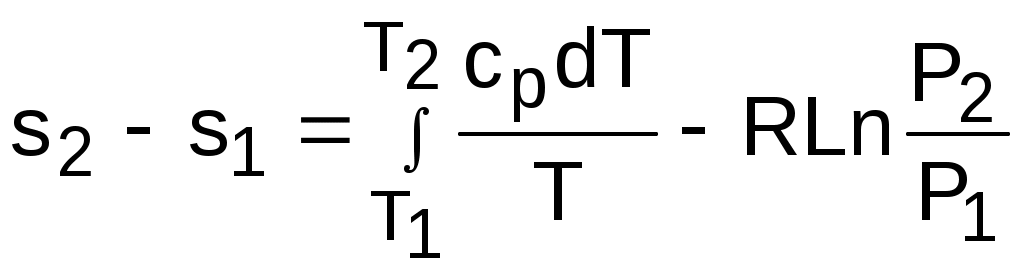 . (4.45) . (4.45)Интегральное слагаемое выражения (4.45) можно представить в виде разности: 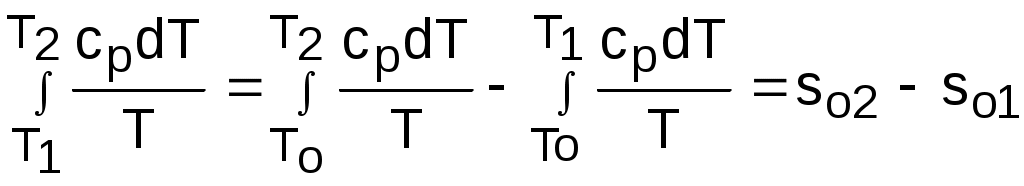 . (4.46) . (4.46)Величины, входящие в эту разность, могут восприниматься как изменение энтропии в зависимости от температуры. Они обозначаются как sо1 и sо2 и могут быть рассчитаны при фиксации То для каждой температуры. Величина so является функцией температуры, а для адиабатного процесса – функцией o и o. В таблицах [12] so рассчитано при То=0 К. Используя табличные значения so, можно определить разницу энтропий в точках по формуле Если требуется абсолютное значение энтропии, необходимо выбрать начало ее отсчета (sо=0) при То и Ро. В качестве То и Ро могут быть приняты любые величины. В случае выбора То=0 К, как и в таблицах [12], получим расчетное выражение абсолютной энтропии, например, для точки с Р1 и Т1: где 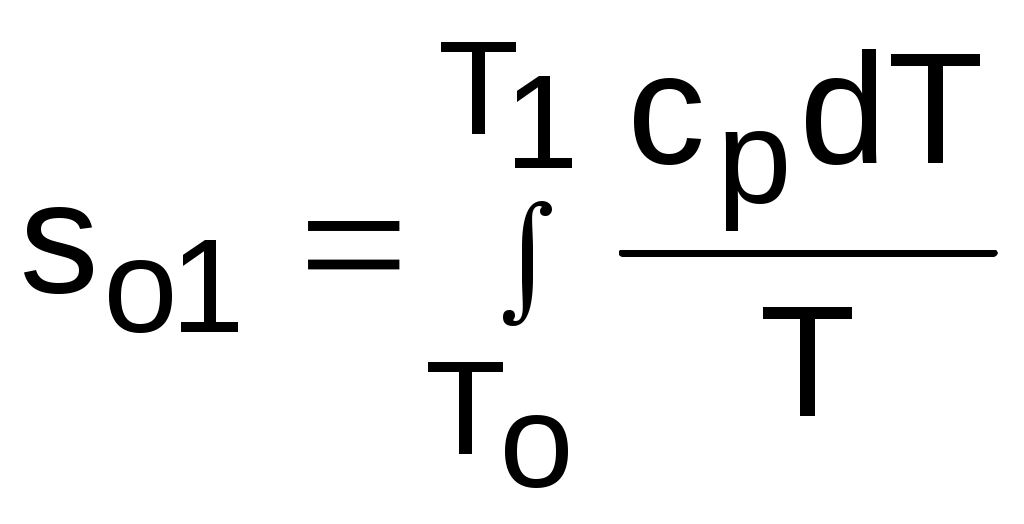 , , 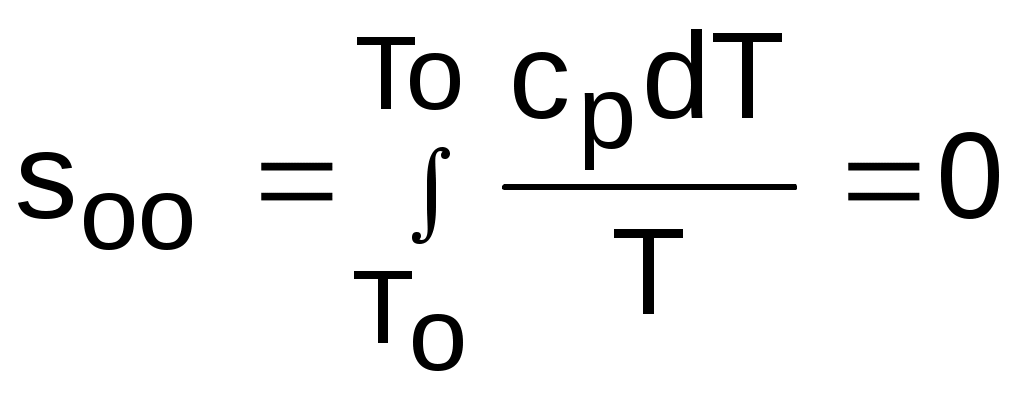 . .При несоответствии То значению абсолютного нуля для определения sо1 и абсолютной энтропии s1 в выражении (4.48) появится дополнительное постоянное вычитаемое которое уменьшит абсолютное значение энтропии s1, но не скажется на величине изменения энтропии s2-s1. То есть значение температуры, принятое для начала отсчета абсолютной энтропии, не обязательно должно соответствовать базовой температуре То, принятой для расчета табличных величин sо. Также произволен и выбор значения Ро для расчета абсолютного значения энтропии. Величины cp, cv, u, h, so, o, o, рассчитанные по формулам (4.32) – (4.45) для различных газов, сводятся в специальные таблицы [12] термодинамических свойств газов. В этих таблицах приводятся величины cp, cv, u, h, so, o, o – в зависимости от температуры. Для расчета адиабатного процесса можно пользоваться всеми приведенными в таблице величинами. Для расчетов других процессов можно пользоваться только величинами cp, cv, u, h, so как функциями от температуры. Приведем пример использования этих таблиц для расчетов процессов газов, подчиняющихся уравнению Pv=RT. Пусть требуется рассчитать обратимый адиабатный процесс сжатия воздуха от состояния Р1=1 бар и t1=17 оС до давления Р2=10 бар, а затем рассчитать количество теплоты и изменение энтропии при охлаждении воздуха при постоянном давлении Р2=const от t2 до t3=20 оС (рис.4.17). Решение По таблицам термодинамических свойств воздуха [9, 12] определяем 01 по известной температуре t1=17 oC. Определив 01=1,2339, рассчитываем 02 по известному отношению давлений адиабатного процесса: П 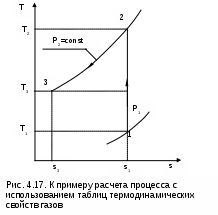 о величине 02 определяем по таблицам [9, 12] температуру в конце адиабатного процесса: t2 = 283 oC (взято с точностью до 1о). Зная температуры во всех трех точках сложного процесса, определим по ним из таблиц необходимые для расчета энергетические параметры: h1=290,28 кДж/кг, u1=207,01 кДж/кг, h2=561,13 кДж/кг, u2=401,52 кДж/кг, h3=293,29 кДж/кг, u3=209,16 кДж/кг. Для адиабатного процесса 12 определим: h2 - h1 = 561,13 - 290,28 = 270,85 кДж/кг, u2 - u1 = - = 401,52 - 207,01 = 199,51 кДж/кг. Для изобарного процесса 23 количество теплоты рассчитывается как разница его энтальпий: q23 = h3 - h2 = 293,29 - 561,13 = - 267,84 кДж/кг. Для определения изменения энтропии в процессе 23 из таблиц по t2 и t3 возьмем sо2=7,3298 кДж/(кг·К) и sо3=6,6789 кДж/(кг·К) и рассчитаем изменение энтропии: Изменение энтропии происходит только за счет изменения температуры, т.к. процесс 23 – изобарный. Для определения абсолютных значений энтропий необходимо задаться величиной Ро. Приняв Ро=1 бар, рассчитаем s1, s2 и s3: т.к. в пределах погрешности расчетов s1=s2, то это подтверждает, что процесс 12 адиабатный. Проверим ранее полученное значение разности энтропий s3-s2 по разности абсолютных энтропий в этих точках: s3 - s2 = 6,0181 - 6,6689 = - 0,6508 В этом случае сходимость результатов тоже очевидна. 5. РЕАЛЬНЫЕ ГАЗЫ И ПАРЫ 5.1. Термические свойства реальных газов Реальные газы отличаются от своей модели – идеальных газов – тем, что их молекулы имеют конечные размеры и между ними действуют силы притяжения (при значительных расстояниях между молекулами) и отталкивания (при сближении молекул друг с другом).Характер изменения этих сил взаимодействия в зависимости от расстояния между центрами молекул r показан на рис. 5.1. На рис. 5.2 в Р,v- диаграмме представлена изотерма реального вещества 1234 и изотерма идеального газа ав. Характер поведения изотермы реального вещества 1234 (рис.5.2) можно частично объяснить характером изменения сил взаимодействия между молекулами (см. рис.5.1) в зависимости от расстояния между их центрами при изменении давления, считая, что на обоих рисунках линии 1234 соответствует одна и та же изотерма. В точке 1 при малых давлениях расстояние между молекулами большое (очень), здесь действуют небольшие силы взаимного притяжения молекул. На участке 12 при увеличении давления газ сжимается, объем его уменьшается. По мере увеличения давления и уменьшения объема молекулы сближаются, силы притяжения возрастают и достигают максимума в точке 2. Силы взаимного притяжения молекул обусловливают появление внутреннего давления, которое возрастает по мере сближения молекул и приводит к более интенсивному изменению объема газа. Действие сил притяжения молекул в точке 2 аналогично действию пружины, которая полностью растянута. Далее, начиная с точки 2 и до точки 3 (рис.5.2), газ будет переходить в жидкую фазу, т.е. здесь одновременно существуют газовая и жидкая фазы при одинаковых давлениях и температурах. В отношении двух молекул это динамичный процесс сближения, и двух фаз здесь быть не может (рис.5.1), в точке 2 был газ, а в точке 3 стала жидкость. При этом силы взаимного притяжения молекул уменьшаются, и в точке 3, где весь газ вступил в жидкую фазу, силы притяжения уравновешиваются силами отталкивания (условная пружина находится в свободном состоянии, не сжата и не растянута). У 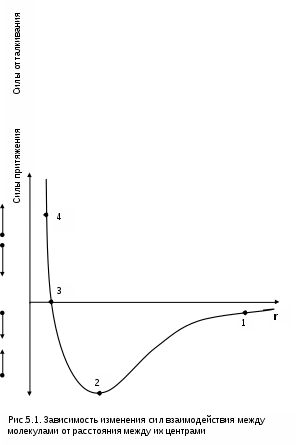 меньшение объема в процессе 23 (рис. 5.2), с одной стороны, обусловлено внутренним давлением, которое падает в среднем до нуля в точке 3, а с другой стороны, объясняется образованием жидкой фазы, т.е. по мере увеличения капелек жидкости в смеси уменьшается количество газа, для газа объем соответствует точке 2, а для жидкости – точке 3, в результате удельный объем смеси при фазовом переходе уменьшается от точки 2 до точки 3. П 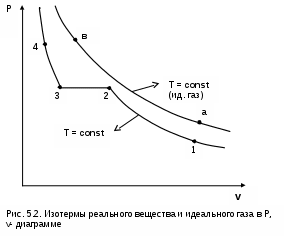 ри дальнейшем увеличении давления (процесс 34 на рис.5.1 и 5.2) сжимается только жидкая фаза, при этом расстояния между молекулами настолько малы, что преобладают силы отталкивания, т.к. на сжатие уже оказывает влияние собственный объем молекул, соизмеримый со свободным объемом жидкой фазы. То есть собственный объем молекул оказывает противоположное воздействие силам взаимного притяжения (условная пружина полностью сжата). В результате этого воздействия дальнейшее увеличение давления не приводит к значительному уменьшению объема жидкой фазы, т.е. жидкость – плохо сжимаемая фаза вещества. Переход веществ из газообразного состояния непосредственно в жидкое при атмосферных условиях возможен не для всех веществ. Например, двуокись углерода СО2 поддавалась этому переводу, а воздух, кислород, азот – нет. Поэтому долгое время жидкая и газообразная фазы вещества рассматривались как принципиально различные с различными свойствами, как твердая и жидкая фазы. Причина такой разницы в поведении газов была не ясна. Позднее было установлено, что такой фазовый переход можно обнаружить для всех газов, но для некоторых из них он достигается при очень низких температурах. Эта точка зрения коренным образом изменилась после опытов, проведенных английским физиком Т. Эндрюсом в 1857–1869 гг. [10]. Эндрюс экспериментально исследовал Р,v,T - зависимости для двуокиси углерода (углекислоты) СО2, подвергая ее сжатию при различных постоянных температурах. Полученные в результате экспериментов зависимости представлены на рис. 5.3. П 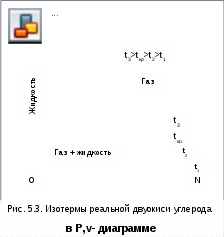 ри сравнительно низкой температуре с повышением давления сначала объем плавно уменьшается. При достижении определенного для каждой температуры давления объем уменьшается без изменения давления, при этом в прозрачной трубке, где находится СО2, можно визуально наблюдать переход газа в жидкость при наличии поверхности раздела фаз. После превращения всей газовой фазы в капельную жидкость дальнейшее повышение давления незначительно сказывается на изменении объема, и изотерма резко поднимается вверх. При повышении температур давление фазового перехода повышается, а разность удельных объемов в начале и в конце этого перехода, т.е. горизонтальный участок изотермы в Р,v - диаграмме, уменьшается. При определенной температуре, называемой критической, этот горизонтальный участок исчезает совсем, а при более высоких температурах (t3) изотермы протекают монотонно без видимого фазового перехода. Опытами Эндрюса и последующими исследованиями других ученых была установлена непрерывность газообразного и жидкого состояния вещества, было доказано, что нет резкой границы между физическими свойствами этих фаз. Можно, обойдя критическую точку сверху, перейти из области жидкости в область газовой фазы или наоборот без видимого фазового перехода. Газ и жидкость являются изотропнымифазами вещества с одинаковым характером молекулярных взаимодействий и беспорядочным движением микрочастиц. В отличие от газа и жидкости твердое кристаллическое вещество является анизотропным. Переход кристаллического вещества в жидкость без видимого фазового перехода не удается получить при любых доступных для воспроизведения давлениях. Для некоторых веществ, изоэнтропных, некристаллических в твердом состоянии: стекла, парафина, гудрона и т.п., – допустим переход из твердой фазы в жидкую и наоборот, без видимого скачка свойств. Эти вещества иногда называются твердыми жидкостями. Для них возможно сразу перейти из жидкой фазы в твердую, и наоборот. Важнейшими термодинамическими характеристиками вещества являются параметрыего критического состояния:Ркр, Tкр, vкр. Они неодинаковы для различных веществ и выражают в обобщенной количественной форме эффект действия молекулярных сил. На критической изотерме, проходящей через точку К, горизонтальный участок имеет нулевую длину, т.е. здесь нет разницы плотностей жидкой и газовой фаз. Превращение жидкости в пар при Р<Ркр требует затраты теплоты парообразования. В критической точке при Ркр теплота парообразования нулевая, ее нет. Критическая точка для критической изотермы в Р,v- координатах является точкой перегиба, в этой точке касательная к изотерме представляет собой горизонталь, и, следовательно, для критической точки 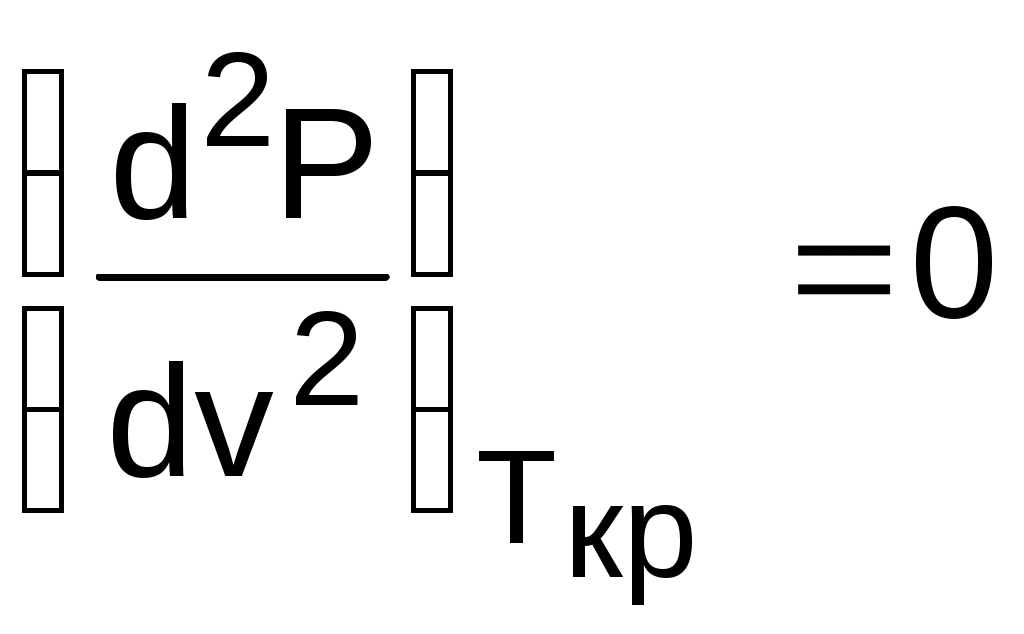 . .Сверхкритические изотермы (Т>Ткр) в Р,v- диаграмме не имеют горизонтальной касательной, для них всегда (dР/dv)T<0. Для изотерм, близких к критической, характерно наличие перегиба, постепенно исчезающего с повышением температуры. Для некоторых веществ критические параметры приведены в табл. 5.1. |
