пособие. ТТД ч1 учебное пособие. Техническая термодинамика

• Название: Техническая термодинамика
• Анкор: пособие
• Дата: 02.02.2023
• Размер: 4.15 Mb.
• Имя файла: ТТД ч1 учебное пособие.doc
• Тип: Учебное пособие; #917693
• страница: 6 из 19

Теплоемкости процессов

Поскольку теплота является функцией процесса, то и теплоемкость есть функция процесса. На практике наибольшее применение нашли теплоемкости изобарного – c_p при Р=const и изохорного – c_v при v=const процессов.

Теплоемкости идеальных газов

Воспользуемся первым законом термодинамики для получения аналитических выражений изохорной и изобарной теплоемкостей идеальных газов:

c = q/dT = du/dT + /dT = du/dT + Pdv/dT . (3.21)

При v=const (dv=0) из выражения (3.21) получим аналитическое выражение для изохорной теплоемкости:

с_v = (du/dT)_v . (3.22)

Подставив с_v в выражение дифференциала внутренней энергии при независимых переменных T и v, получим выражение

du = (du/dT)_vdT + (du/dv)_Tdv = c_vdT + (du/dv)_Tdv . (3.23)

Для идеального газа внутренняя энергия – функция только одного термического параметра – температуры, т.е. (du/dv)_T=0. Следовательно, для идеального газа выражение (3.23) примет вид

du = c_vdT . (3.24)

Аналитическое выражение изохорной теплоемкости идеального газа получается из (3.24) и выражения внутренней энергии идеального газа: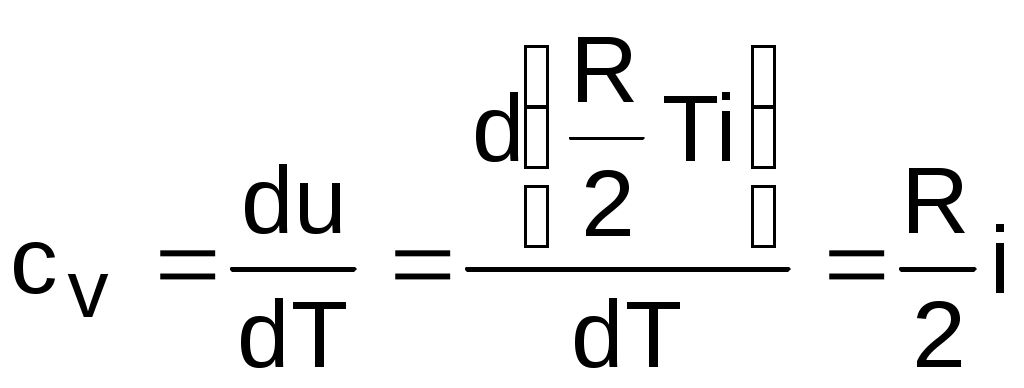

. (3.25)

Из выражения (3.25) следует, что изохорная теплоемкость идеального газа величина постоянная.

Подставив выражение изохорной теплоемкости идеальных газов (3.25) в уравнение (3.21), получим выражение теплоемкости идеального газа в виде

c = c_v + Pdv/dT . (3.26)

Рассмотрим выражение (3.26) применительно к идеальному газу для изобарного процесса P=const. Второе слагаемое выражения (3.26) для идеального газа при P=const можно получить дифференцированием уравнения Менделеева – Клапейрона:

Pv=RT , при Р=const Pdv=RdT  Pdv/dT=R .

В результате этих преобразований получаем расчетное выражение для изобарной теплоемкости идеального газа:

c_p = c_v + R . (3.27)

Уравнение (3.27) носит название формула Майера. Используя формулу Майера, получим аналитическое выражение изобарной теплоемкости идеального газа:

. (3.28)

Изобарная теплоемкость идеального газа больше изохорной теплоемкости на величину газовой постоянной.

Аналитические выражения для удельных мольных и объемных изохорных и изобарных теплоемкостей идеального газа легко получить, используя их взаимосвязь с удельными массовыми теплоемкостями (3.25) и (3.28):

Дж/(кмольК); (3.29)

Дж/(кмольК); (3.30)

, Дж/(нм³К); (3.31)

Дж/(нм³К). (3.32)

В соответствии с молекулярно-кинетической теорией идеальных газов их изобарные и изохорные теплоемкости (выражения (3.25), (3.28) – (3.32)) – величины постоянные, не зависящие от термических параметров состояния газа.

В системе единиц, основанной на калории (1ккал=4187кДж) мольная теплоемкость идеального газа определяется простым соотношением (ккал/(кмольК)):

c_v  i ; (3.33)

c_p  (i+2) . (3.34)

Теплоемкость реальных газов

Для реальных газов теплоемкости c_v и с_p зависят от давления и температуры газа. Это обусловлено наличием сил межмолекулярного взаимодействия, изменением взаимного положения атомов в молекулах (молекулы двух - и многоатомных газов не жесткие, присутствует колебательное движение атомов в молекуле) и неравномерным распределением внутренней энергии по степеням свободы в зависимости от изменения температуры и давления газа.

З ависимость теплоемкости газов от давления в большей степени проявляется в состоянии газов, близком к области насыщения (см. разд. 6). Для газов, состояние которых далеко от области насыщения, зависимость теплоемкости от давления незначительна и при практических расчетах ею пренебрегают. Зависимость от температуры очень существенна, ей пренебрегать при точных расчетах нельзя.

Аналитическое выражение этой зависимости весьма сложное и требует нахождения целого ряда экспериментальных констант для каждого газа. Практическое определение теплоемкостей с_v и с_p реальных газов ведется экспериментально. В соответствии с этим были введены понятия истинной и средней теплоемкости газа.

Истинная теплоемкость газа соответствует расчетному выражению

, (3.35)

она определяется как частное от деления элементарной теплоты процесса на элементарное изменение его температуры относительно точки процесса с фиксированной температурой (рис.3.2). Для реальных газов каждому значению температуры процесса соответствует вполне определенное значение истинной теплоемкости.

Экспериментальная зависимость истинной теплоемкости процесса реального газа от температуры обычно представляется в виде степенного полинома графика (см. рис.3.2) или табличного численного материала.

с = а + b₁t + b₂t² + b₃t³ +  + b_ntⁿ . (3.36)

Определение теплоты с помощью истинной теплоемкости ведется интегрированием: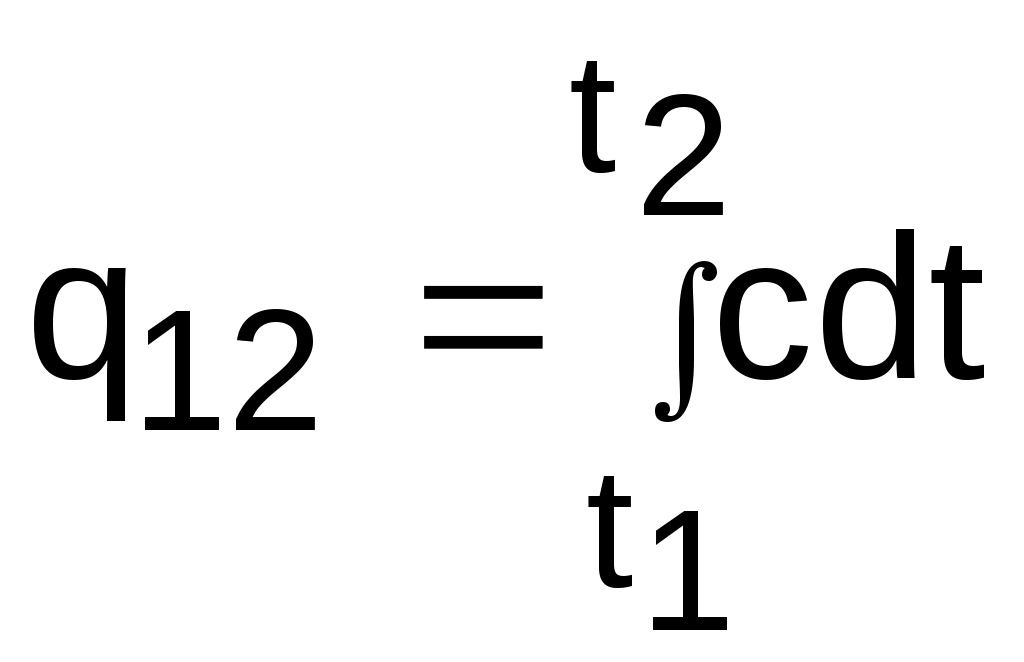

. (3.37)

Теплота q₁₂ на рис.3.3 соответствует площади под процессом 12. Средняя теплоемкость газа соответствует расчетному выражению

, (3.38)

она определяется как теплота процесса, идущего в интервале температур t₁ и t₂, деленная на разность этих температур (рис.3.3).

Средней теплоемкостью можно пользоваться только на данном интервале температур. Это очень неудобно, т.к. для практических расчетов необходимо в таблицах экспериментальных данных по средним теплоемкостям предусмотреть все возможные температурные интервалы. Выход из этой ситуации был найден введением средней теплоемкости, определенной от одинаковой начальной температуры. В качестве такой температуры приняли 0 ^оС. Расчетное выражение средней теплоемкости, определенной от 0 ^оС, имеет вид

. (3.39)

Используя эту теплоемкость, можно определить теплоту и среднюю теплоемкость в любом интервале температур процесса (рис.3.3). Площадь под процессом А1 соответствует теплоте q₀₁=c_m01t₁, а под процессом А2 – теплоте q₀₂=c_m02t₂, теплота процесса 12 определяется как разность этих площадей:

q₁₂ = q₀₂ - q₀₁ = c_m02t₂ - c_m01t₁ . (3.40)

Следовательно, средняя теплоемкость на интервале температур t₁ и t₂ будет определяться как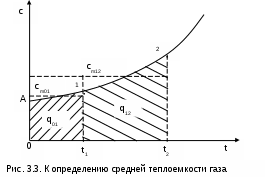


. (3.41)

В справочных таблицах свойств газов даются значения истинных теплоемкостей при конкретных температурах и средних теплоемкостей в интервале от 0 до t ^оС. Экспериментально проще определяются изобарные теплоемкости газов. Изохорные теплоемкости газов, подчиняющихся уравнению Pv=RT, рассчитывают по формуле c_v=c_p-R (Майера). Удельные мольные и объемные теплоемкости реальных газов рассчитываются по их соотношениям с удельными массовыми теплоемкостями.

Отношение изобарной и изохорной теплоемкостей

При расчетах газовых процессов часто используется коэффициент, представляющий отношение изобарной и изохорной теплоемкостей газов: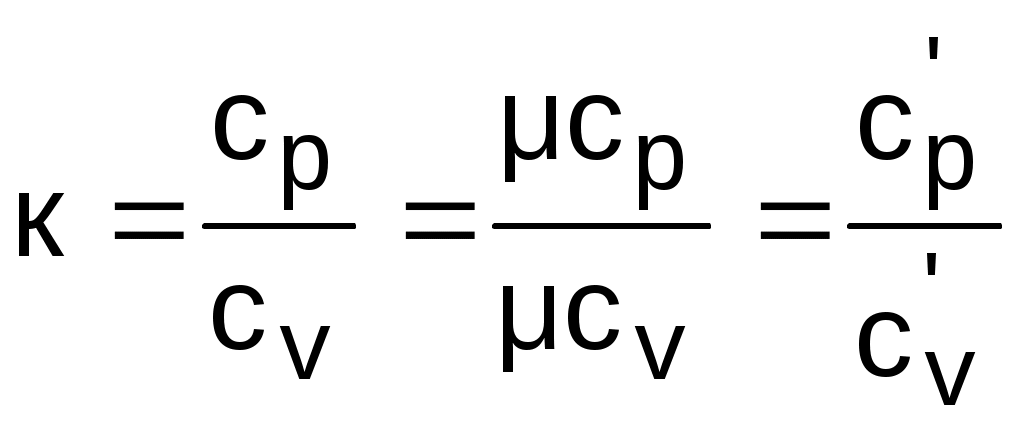

. (3.42)

Этот коэффициент носит название коэффициента Пуассона. Для идеальных газов с постоянными темлоемкостями с_p и с_v это величина постоянная:

, (3.43)

для одноатомных газов i=3, к=5/3=1,667;

для двухатомных i=5, к=7/5=1,4;

для многоатомных i=6, к=8/6=1,333.

Для реальных двух - и многоатомных газов, подчиняющихся уравнению Pv=RT, коэффициент Пуассона так же, как и теплоемкости, зависит от температуры. С повышением температуры у них к уменьшается, это следует из зависимости

к= c_p/c_v = (c_v + R)/c_v = 1 + R/c_v, (3.44)

поскольку с увеличением температуры изохорная теплоемкость реального газа увеличивается.

3.1.3. Энтальпия идеальных газов

Энтальпия h = u + Рv, как любой параметр состояния, может быть определена через любую пару независимых параметров состояния. Выразим полный дифференциал энтальпии, используя при его определении в качестве независимых термических параметров Р и Т:

. (3.45)

Для изобарного процесса при Р=const, используя первый закон термодинамики, получим выражение

dq_p = c_pdT = (dh - vdР)_p = dh_p, (3.46)

в соответствии с которым изобарная теплоемкость определяется как

. (3.47)

Применив уравнение (3.47) к (3.46), получим выражение для определения элементарного изменения энтальпии реальных веществ:

. (3.48)

Для этальпии идеального газа, подчиняющегося уравнению Pv=RT, будет выполняться равенство

, (3.49)

т.е. энтальпия идеальных газов не зависит от давления, а выражение (3.48) для идеальных газов примет вид

dh = c_pdT. (3.50)

Поскольку изобарная теплоемкость идеальных газов величина постоянная, то энтальпия идеальных газов есть функция только температуры. В свою очередь, для изобарной теплоемкости идеального газа не зависимо от процесса справедливо выражение

. (3.51)

Абсолютное значение энтальпии можно получить интегрированием выражения (3.48). При этом необходимо выбрать начало ее отсчета, приняв h_o при фиксированных параметрах газа Р_о и Т_о.

или . (3.52)

Необходимо помнить, что начало отсчета энтальпии и внутренней энергии связаны соотношением

h_o = u_o + P_ov_o , (3.53)

в соответствии с которым, приняв u_o=0, получим h_o = P_ov_o, т.е. начало отсчета энтальпии будет больше нуля.

При различных значениях Р_о и Т_о будут различными и абсолютные значения энтальпии. Однако в расчетах процессов используется разница энтальпий, а не их абсолютные значения. Для разницы энтальпий процесса выбор параметров начала отсчета энтальпии никакой роли не играет:

. (3.54)

Прокомментируем расчет абсолютного значения энтальпии на примере идеального газа. Примем начало отсчета энтальпии идеального газа h_o при 0 ^оС. Приняв при 0 ^оС u_o=0, получим h_o=u_o+P_ov_o=RT_o=273,15R, тогда абсолютное значение энтальпии вычисляется по формуле

h-h_o=c_p(t-0) или h=c_pt+h_o=c_pt+273,15R. (3.55)

Приняв начало отсчета энтальпии и внутренней энергии идеального газа от абсолютного нуля Т_о=0 К и задав u_o=0, получим h_o=P_ov_o=RT_o=0R=0, т.е. в данном случае численные значения начала отсчета внутренней энергии и энтальпии одинаковы и равны нулю. Расчетное выражение абсолютной энтальпии в этом случае будет представлено в виде

h - h_o = h - 0 = c_p(T-0) или h = c_pT . (3.56)

Абсолютные значения энтальпий по выражениям (3.55) и (3.56) при одинаковых температурах будут разные, но разница энтальпий в одинаковом интервале температур будет одинаковой:

h₂ - h₁ = c_p(t₂-t₁) = c_p(T₂-T₁) . (3.57)

Таким образом, в расчетах абсолютного значения энтальпии основным требованием является необходимость выбора одинаковых параметров для принятия начала отсчета внутренней энергии и энтальпии. Для идеального газа начало отсчета энтальпии и внутренней энергии фиксируется только температурой.

При расчете разности энтальпий выбор параметров начала отсчета энтальпии никакой роли не играет. Поэтому, если сразу рассчитывается разность энтальпий (выражение (3.55), то параметры начала отсчета энтальпии вообще не нужны, если разница энтальпий определяется через их абсолютные значения h₂ - h₁, то они должны иметь одинаковые (любые) параметры начала их отсчета.

3.1.4. Энтропия идеальных газов

Для получения расчетного выражения изменения энтропии идеальных газов воспользуемся первым законом термодинамики, в котором теплота определяется с использованием изменения энтальпии:

. (3.58)

Для идеального газа изменение энтальпии определяется как dh=c_pdT, а удельный объем v = RT/P. Подставив данные выражения изменения энтальпии и удельного объема в уравнение (3.58), получим уравнение для изменения энтропии идеального газа:

. (3.59)

Разность энтропий идеального газа в конкретных точках можно получить интегрированием выражения (3.59):

. (3.60)

Воспользовавшись формулой Майера с_p=с_v+R и уравнением Менделеева – Клапейрона Pv=RT, выражение (3.60) можно записать и через две другие пары термических параметров состояния:

. (3.61)

Для определения абсолютного значения энтропии идеального газа необходимо зафиксировать начало ее отсчета любой парой термических параметров состояния. Например, приняв s_о=0 при Т_о и Р_о, воспользовавшись уравнением (3.60), получим

. (3.62)

Выражение (3.62) свидетельствует о том, что энтропия идеального газа есть параметр состояния, поскольку ее можно определить через любую пару параметров состояния. В свою очередь, поскольку энтропия сама является параметром состояния, используя ее в паре с любым независимым параметом состояния, можно определить любой другой параметр состояния газа.

3.2. Газовые смеси

В практической деятельности чаще всего имеют дело не с однородными газами, а с их смесями (воздух, продукты сгорания топлива, горючие газовые смеси и т.п.). Поэтому в теплотехнике газовые смеси имеют важное значение.

В объеме, занимаемом газовой смесью, каждый газ, входящий в эту смесь, ведет себя так же, как вел бы себя при отсутствии других составляющих смеси: распространяется по всему объему; создает давление (парциальное), определяемое температурой и объемом на единицу его массы; имеет температуру смеси.

Смесь идеальных газов представляет собой идеальный газ, для которого справедливы законы и полученные для идеальных газов зависимости.

Для идеального газа давление определяется выражением (3.1):

.

Количество молекул, входящих в данную смесь газов, равно сумме молекул газов, составляющих смесь:

n_см = n₁ + n₂ + ··· + n_n . (3.63)

Произведение mw²=2T пропорционально абсолютной температуре газа, а поскольку все газы, входящие в смесь, имеют одинаковую температуру, то справедливо равенство

2T = m₁w₁² = m₂ w₂² = ··· = m_n w_n² . (3.64)

В соответствии с выражениями (3.63) и (3.64) давление для смеси газов можно представить в виде суммы



, (3.65)

где P_i – парциальные давления газов, составляющих смесь.

Уравнение (3.65) представляет математическое выражение закона Дальтона (1807 г.) в соответствии с которым давление газовой смеси равно сумме парциальных давлений газов, входящих в смесь.

Парциальное давление – это давление, которое создает один из газов, составляющих смесь, при температуре смеси в случае заполнения им всего объема смеси. Парциальное давление – это реально-существующая величина, поскольку каждый отдельный газ в смеси имеет температуру смеси и занимает весь объем смеси. Парциальное давление можно определить из уравнения Менделеева –Клапейрона:

, (3.66)

где V_см – объем, занимаемый всей смесью газов;

m_i – масса отдельного газа, входящего в смесь;

R_i– газовая постоянная отдельного газа;

T_см – температура смеси газов.