пособие. ТТД ч1 учебное пособие. Техническая термодинамика

• Название: Техническая термодинамика
• Анкор: пособие
• Дата: 02.02.2023
• Размер: 4.15 Mb.
• Имя файла: ТТД ч1 учебное пособие.doc
• Тип: Учебное пособие; #917693
• страница: 5 из 19

Длительное время природу теплоты объясняли с помощью ложной теории теплорода. Единица измерения теплоты была только в калориях, эквивалента теплоты и механической работы не было. Одинаковую природу теплоты и механической работы доказал английский физик Д.Джоуль в 1843–1850 гг. [7]. Он же определил эквивалент механической и тепловой работы (1 ккал = 427 кгм).

Д 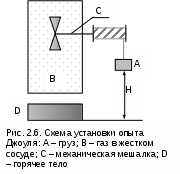жоуль провел следующий опыт (рис. 2.6). В замкнутый жесткий сосуд В с газом, исключающий механическое взаимодействие газа и внешней среды путем изменения объема газа, поместили мешалку. Механическое взаимодействие газа с внешней средой (без изменения объема газа) может осуществляться вращением мешалки, приводимой в действие за счет опускания груза А. Тепловое взаимодействие газа с внешней средой может осуществляться с помощью его контакта с телом D, имеющим температуру большую, чем у газа (t_D>t_B).

Изменение состояния газа в сосуде (например, ориентируясь на температуру и давление) можно осуществить двумя способами: механическим – путем вращения мешалки, и тепловым – нагревая газ с помощью тела D. В обоих случаях будет происходить изменение внутренней энергии газа. Джоуль добился одинакового изменения состояния газа механическим и тепловым взаимодествиями газа с внешней средой, т.е. в начале и в конце каждого энергетического взаимодействия параметры газа были одинаковы, например P₁ и t₁, P₂ и t₂. Поскольку одинаковы начальные и конечные состояния газа в обоих опытах, то одинаково и изменение внутренней энергии газа в этих опытах. Исходя из этого, можно записать:

U₂ - U₁ = -L' = mgH, U₂ - U₁ = Q, -L' = Q. (2.28)

В соответствии с выражением (2.28) получили эквивалентность механической работы, произведенной над газом, и теплоты, подведенной к газу.

Единицы измерения теплоты и механической работы расширения в СИ одинаковы – джоуль (Дж), поэтому в данной системе единиц выражение первого закона термодинамики не требует ввода эквивалента между единицами теплоты и работы, как это была в XXIX веке.

2.4.1. Аналитические выражения первого закона

термодинамики.

Уравнение первого закона термодинамики (2.27) обычно записывается с расположением теплоты в левой части, а изменения внутренней энергии и работы расширения в правой:

Q = U₂ - U₁ + L' . (2.29)

Для одного килограмма вещества оно примет вид

q = u₂ - u₁ + l' . (2.30)

Это интегральная форма записи первого закона термодинамики, т.е. целиком для всего процесса, происходящего с веществом от состояния 1 до состояния 2.

Дифференциальная форма записи первого закона термодинамики, будет иметь вид

Q = dU + L' , (2.31)

q = du + ' . (2.32)

В этих уравнениях величинами L' и l' обозначается работа изменения объема, совершаемая телом в реальных необратимых процессах. Работа расширения увеличивает механическую энергию системы, т.е. она может передаваться или внешнему потребителю работы, или внешней среде.

При обратимых процессах вся работа изменения объема тела затрачивается на преодоление внешнего давления и аккумулируется системой в форме механической энергии. Расчетное выражение работы изменения объема обратимого процесса было получено ранее в виде

 = Pdv .

При необратимых процессах изменения объема тела имеет место трение. Например, трение газа о стенки емкости или расширение газа идет с образованием вихревого движения. Трение приводит к увеличению внутренней энергии тела (оно нагревается). Поэтому внешняя работа расширения оказывается меньше работы изменения объема обратимого процесса на величину работы трения:

' =  - _тр = Pdv - _тр . (2.33)

Здесь  и ' – работа обратимого и необратимого процессов;

_тр – работа трения.

Работа трения _тр переходит в конечном результате в теплоту трения dqтр. Тогда первый закон термодинамики для необратимого процесса расширения тела можно записать в виде

q = du +  - _тр = du +  - q_тр,

перегруппировав члены данного уравнения, окончательно получим

q* = q + q_тр = du + = du + pdv, (2.34)

где q* – полная теплота, полученная телом в необратимом процессе.

Для обратимых процессов q_тр=0, и первый закон термодинамики обратимого процесса будет иметь вид

q = du +  = du + pdv. (2.35)

Поскольку внутренняя энергия может быть представлена в виде функции любой пары независимых параметров состояния (она сама параметр состояния), то выражение (2.35) можно записать в виде частных производных от этих параметров состояния. Например, выразив du в частных производных от P и v, получим выражения

du = (u/p)_vdp + (u/v)_pdv , (2.36)

q = (u/p)_vdp + [(u/v)_p + p]dv. (2.37)

Таких уравнений можно записать столько, сколько существует пар независимых параметров состояния. Значение дифференциальных уравнений первого закона термодинамики очень велико, поскольку, зная функциональную взаимосвязь термических параметров состояния вещества (Р,v,T), используя эти дифференциальные уравнения, можно рассчитать энергетические параметры данного вещества (u, s и т.п.) и его теплоемкости, а также решать и обратную задачу.
2.4.2. Энтальпия

Многие термодинамические расчеты облегчаются при использовании аддитивных свойств термодинамических тел, называемых энергетическими или калорическими параметрами состояния. Такое название эти параметры состояния получили потому, что в их единицах измерения присутствует величина энергии (Дж) или (ккал). С некоторыми из них мы уже познакомились: это энтропия S(Дж/К) и внутренняя энергия U(Дж). Теперь познакомимся с энтальпией.

Преобразуем выражение первого закона термодинамики (2.35), записав его в виде

q=du+Pdv=du+d(Pv)-vdP=[d(Pv)=vdP+Ppdv]=d(u+Рv)-vdp. (2.38)

В равенстве (2.38) сумма (u + Рv) является функцией состояния или параметром состояния, ее назвали энтальпией и обозначили буквой h:

h = u + Рv . (2.39)

В выражении (2.39) h – удельная энтальпия, для всей массы тела полная энтальпия обозначается буквой H и рассчитывается как

H = mh = U + РV . (2.40)

Полная энтальпия H обладает свойствами аддитивности (суммирования), т.к. внутренняя энергия U и объем V – величины экстенсивные, а давление Р – величина интенсивная. Удельная энтальпия h обладает свойствами интенсивной величины. Энтальпия относится к энергетическим (калорическим) параметрам.

Э 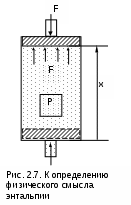нтальпия имеет определенный физический смысл [7]. Прокоментируем физический смысл энтальпии с помощью рис. 2.7. В цилиндре с поршнем находится газ при давлении Р. Силовое воздействие давления газа на поршень уравновешивается внешним силовым воздейсвием F, т.е. система находится в равновесном состоянии. Энергию газа такой системы можно представить в виде суммы двух энергий: внутренней энергии газа – U и потенциальной энергии газа, которая характеризуется работой внешних сил, уравновешивающих давление газа, затраченных на заполнение газом данного объема.

Получение потенциальной энергии газом может быть проиллюстрировано в виде работы внешних сил, затраченной на перемещение поршня в цилиндре, в случае заполнения его газом при постоянном давлении от нулевого объема V=0 до объема V. Поскольку при заполнении газом цилиндра над газом со стороны окружающей среды была совершена работа, то энергия газа увеличилась на величину этой работы. Это потенциальная энергия давления газа, которая рассчитывается как произведение внешней силы F на перемещение поршня x или как произведение давления газа на изменение его объема от 0 до V:

Fx = P(V - 0) = PV .

В итоге получили, что полная энергия такой системы есть сумма U+PV, а это и есть энтальпия H=U+PV.

Таким образом, энтальпия есть полная энергия расширенной системы, представляющяя сумму внутренней энергии и внешней – потенциальной энергии давления.

Как любой параметр состояния, энтальпия может быть определена любой парой независимых параметров состояния.

Используя понятие энтальпии, первый закон термодинамики можно записать в виде

q = dh - vdР , (2.41)

Q = dH - VdР. (2.42)

Из выражения (2.41) видно, что энтальпией удобно пользоваться при определении теплоты в изобарных процессах (Р=const): q_p=dh_р.

Изобарная теплоемкость тела тоже может быть рассчитана с использованием величины изменения энтальпии:

с_p = q_p/dT = (h/T)_p . (2.43)

Необходимо обратить внимание на то, что выражение (2.43) справедливо только для изобарных процессов, т.е. разность энтальпий можно рассчитать как произведение изобарной теплоемкости на изменение температуры только при Р=const: dh_p=c_pdT. В общем случае изменение энтальпии можно представить как полный дифференциал, выраженный через частные производные энтальпии от любой пары независимых параметров состояния. Например, выразим изменение энтальпии через ее зависимость от давления и температуры:

dh = (h/T)_pdT + (h/P)_TdP , (2.44)

используя выражение (2.43) для первого слагаемого, получим

dh = c_pdT + (h/P)_TdP . (2.45)

При определении энтальпии, как и для внутренней энергии, выбирают начало отсчета. Хотя выбор параметров начала отсчета энтальпии произволен, т.к. в термодинамике важно не абсолютное ее значение, а разность, необходимо иметь в виду, что начала отсчета и внутренней энергии, и энтальпии связаны между собой. Так, если u_о = 0, то при тех же условиях h_о = Р_оv_о > u_о.

В практике широко используется диаграмма h, s. Для нее начала отсчета энтальпии и энтропии выбираются при одинаковых параметрах состояния. С использованием h, s- диаграммы, легко графически представляются и рассчитываются основные процессы в теплоэнергетике: изобарный, адиабатный, а также оцениваются необратимости на трение и дросселирование.
3. ГАЗЫ И ГАЗОВЫЕ СМЕСИ

3.1. Законы идеальных газов

Газы часто используются в тепловых двигателях в качестве рабочего тела. Это обусловлено их свойством изменять объем в широком диапазоне и, следовательно, получать работу расширения. Знать свойства газов очень важно, т.к. необходимо анализировать процессы, происходящие с рабочим телом в установках и выбирать наиболее экономичные схемы (циклы) этих установок.

Изучение свойств газов ведется двумя путями: экспериментальным и теоретическим. На начальной стадии изучения свойств газов преобладали экспериментальные исследования. В настоящее время теоритические и экспериментальные исследования проводятся совместно. Подтверждение всех теорий возможно только в результате опыта.

Теоретическое изучение свойств газов ведется сначала на упрощенной их модели – идеальном газе.

Под идеальным газом понимается газ, в котором отсутствуют силы гравитационного взаимодействия между молекулами, образующими газ, а механическое взаимодействие молекул ограничено лишь упругим соударением, сами молекулы при этом представляют идеально упругие материальные точки, не имеющие объема.

В соответствии с определением идеального газа поведение молекул в нем подчиняется законам механики. Созданная на основании этих законов теория идеальных газов получила название молекулярно-кинетической теории идеальных газов.

Согласно этой теории абсолютное давление идеального газа определяется исходя из закона импульсов [7] и рассчитывается как

, (3.1)

где Р – абсолютное давление, Н/м² ;

n – число молекул в 1 м³ газа ;

m – масса одной молекулы, кг;

w – средняя квадратичная скорость поступательного движения молекул, м/с.
Исходя из определения абсолютного давления идеального газа оно соответствует силовому воздействию молекул друг на друга или на окружающую их поверхность, взятому на единицу площади и направленному по нормали к этой поверхности. Величина 1/3 в выражении (3.1) указывает на то, что силовое воздействие молекул идеального газа равномерно распределено по всем степеням свободы поступательного движения молекул (у поступательного движения 3 степени свободы). Это объясняется тем, что число молекул даже в малом объеме очень велико, а их движение хаотично.

Ранее было показано, что кинетическая энергия поступательного движения молекул прямо пропорциональна абсолютной температуре газа:

mw²/2 = T или mw² = 2T .

Воспользовавшись этим соотношением, запишем выражение (3.1) в виде

P = (2/3)nT , (3.2)

умножим правую и левую части уравнения (3.2) на объем газа V:

PV = (2/3)nVT = (2/3)NT , (3.3)

где N = nV – число молекул газа, находящегося в объеме V.

Исходя из выражения (3.3) можно сделать следующие заключения:

1. При одинаковых физических условиях (Р и Т одинаковы) в одинаковых объемах (V=idem) находится одинаковое количество молекул идеальных газов N=idem, независимо от того, какой газ или смесь газов заполняют данный объем.

2. Поскольку масса однородного газа равна произведению массы одной молекулы на число молекул, то в соответствии с заключением 1 плотность идеальных газов  при одинаковых Р и Т пропорциональна их молекулярной массе :

  , / = idem или v = idem. (3.4)

Последнее соотношение выражения (3.4) относится к объему одного моля (киломоля) газа v (м³/кмоль), где  (кг/кмоль) – молярная масса газа. Использование киломоля, а не моля объясняется тем, что все расчетные выражения принято давать в СИ (масса в кг, объем в м³ и т.п.).

В результате второе заключение можно сформулировать так: объем одного киломоля (моля) идеальных газов, имеющих одинаковые Р и Т, одинаков. Обозначив объем одного киломоля газа величиной V_=v, получим

V_ = v = idem.

3. Записав выражение (3.3) для одного киломоля газа, получим соотношение

PV_ = (2/3)N_T , (3.5)

где N_ – число молекул в одном киломоле газа.

Применив два предыдущих заключения к выражению (3.5), получим, что при одинаковых Р и Т один киломоль идеального газа занимает одинаковый объем и содержит в этом объеме одинаковое количество молекул. Следовательно, согласно закону сохранения вещества, количество молекул в киломоле всех идеальных газов при изменении Р и Т не изменится, т.е. это величина постоянная – N_=const.

Несложно догадаться, что все три заключения представляют собой закон Авогадро, а величина N_=6,023610²⁶ (1/кмоль) есть число Авогадро.

В выражении (3.5) произведение (2/3) N_ есть постоянная величина для всех идеальных газов. Эту константу обозначили как R_ и назвали универсальной газовой постоянной.

R_ = (2/3) N_ . (3.6)

Определение универсальной газовой постоянной было осуществлено экспериментально на газах при малых значениях давлений. При малых давлениях расстояния между молекулами газа очень большие, силы межмолекулярного взаимодействия практически отсутствуют, а свойства реальных газов соответствуют свойствам идеальных газов. Известно, что при нормальных физических условиях один киломоль всех газов занимает объем V_о=22,4 (м³/кмоль). Подставив эти параметры (P_о=760 мм рт.ст.=101300 Па и Т_о=273,15 К) в уравнение (3.5), получим численное значение универсальной газовой постоянной и ее единицу измерения:

R_ = P_oV_о/T_o = 10130022,4/273,15 = 8314 Дж/(кмольK.

В окончательном виде уравнение (3.5) можно записать в следующих представлениях:

для киломоля газа

PV_ = R_T , (3.7)

где Р – абсолютное давление, Па;

V_ – объем 1 киломоль газа, м³/кмоль;

R_=8314 Дж/(кмольК) – универсальная газовая постоянная;

Т – абсолютная температура, К.

Поделив правую и левую части уравнения (3.7) на молярную массу , получим уравнение для одного килограмма газа:

Рv= (R_/)T , или Рv=RT , (3.8)

где R= R_/ =8314/ Дж/(кгК) носит название газовой постоянной, в отличие от универсальной газовой постоянной она является константой только для данного газа;

v – удельныйобъем газа, м³/кг.

Умножив правую и левую части уравнения (3.8) на массу m, получим уравнение для m килограммов газа:

Рmv=mRT или РV=mRT , (3.9)

где V – объем, м³, занимаемый m кг газа.

Все три уравнения (3.7), (3.8), (3.9) являются уравнениями состояния идеального газа, выражающими взаимосвязь термических параметров состояния: Р, v (V или V_), T. Эти уравнения называются термическим уравнением состояния идеального газа или по фамилиям авторов, получивших эти уравнения, – уравнением Менделеева – Клапейрона.

Состояние идеального газа определяется любой парой термических параметров из трех – Р, v, T. Третий параметр может быть определен из термического уравнения состояния идеального газа.

Уравнение состояния идеального газа было получено в 1834 г. Клапейроном для одного килограмма газа (3.8), а в 1874 г. – Менделеевым для одного моля газа (3.7). Уравнение состояния идеального газа было выведено на основании экспериментальных закономерностей, полученных в ХVII – XIX вв. учеными, исследовавшими свойства газов при параметрах, близких к атмосферным:

закон Бойля – Мариотта для Т=const: Pv=const,

закон Гей – Люссака для Р=const: v/T=const,

закон Шарля для v=const: T/P=const.

Эти законы являются частными случаями уравнения состояния идеального газа и легко могут быть получены из него.

3.1.1. Внутренняя энергия идеального газа

Исходя из определения идеального газа в нем отсутствует потенциальная составляющая внутренней энергии (отсутствуют силы взаимодействия молекул, кроме ударного). Таким образом, внутренняя энергия идеального газа представляет собой только кинетическую энергию движения его молекул. Ранее (уравнение (1.10)) было показано, что кинетическая энергия поступательного движения молекул газа прямо пропорциональна его абсолютной температуре:

.

Используя выражение универсальной газовой постоянной (3.6), можно определить величину константы :

.

Таким образом, кинетическая энергия поступательного движения одной молекулы идеального газа будет определяться выражением

. (3.10)

В соответствии с кинетической теорией распределение энергии по степеням свободы равномерное. У поступательного движения 3 степени свободы. Следовательно, на одну степень свободы движения молекулы газа будет приходитья 1/3 ее кинетической энергии:

. (3.11)

Для двух, - трех - и многоатомных молекул газа кроме степеней свободы поступательного движения есть степени свободы вращательного движения молекулы (рис.3.1). Для двухатомных молекул газа число степеней свободы вращательного движения равно 2, для трех - и многоатомных молекул – 3.

Поскольку распределение энергии движения молекулы по всем степеням свободы равномерное, а число молекул в одном киломоле газа равняется N_, внутреннюю энергию одного киломоля идеального газа можно получить, умножив выражение (3.11) на число молекул в одном киломоле и на число степеней свободы движения молекулы данного газа:

, (3.12)

где U_ – внутренняя энергия 1 киломоля газа, Дж/кмоль;

i – число степеней свободы движения 1 молекулы газа.

Для 1-атомного газа i = 3, для 2-атомного газа i = 5, для 3-атомного и многоатомного газов i = 6.

Д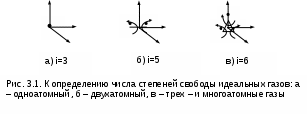
ля многоатомного газа i=6, так как существуют 3 степени свободы поступательного движения и 3 степени свободы вращательного движения молекул. Может быть еще колебательное движение атомов в молекуле, но его обычно учитывают для реальных газов, используя экспериментальные данные. Для идеальных газов колебательное движение атомов в молекулах тоже может быть учтено при расчете внутренней энергии (см. в разд. 4.6). На данном этапе изложения материала будем руководствоваться молекулярно-кинетичесой теорией идеального газа. В соответствии с ней атомы в молекулах идеального газа имеют жесткие связи, т.е. колебательного движения атомов в молекулах нет.

Для одного килограмма идеального газа удельная внутренняя энергия (Дж/кг) определяется делением выражения (3.12) на молярную массу газа:

. (3.13)

Для произвольного количества газа внутренняя энергия определяется как произведение его массы на удельную внутреннюю энергию этого газа:

, (3.14)

где m – масса газа, кг;

U – полная внутрення энергия идеального газа.

Если система состоит из нескольких различных по физическим свойствам газов, то, подчиняясь закону сложения (аддитивности), его полная внутренняя энергия будет определяться суммой внутренних энергий компонентов газовой смеси:

U = m₁u₁ + m₂u₂ +  + m_nu_n , (3.15)

где n – число компонентов газа в системе.

Полученные уравнения внутренней энергии идеального газа (3.12) – (3.15) указывают на то, что внутренняя энергия идеального газа зависит только от абсолютной температуры газа и числа степеней свободы движения его молекул:

u = f(T) или (du/dP)_T = 0, (du/dv)_T = 0. (3.16)
3.1.2. Теплоемкости газов

Понятие теплоемкости рассмотрено в разд. 2.2. Применим это понятие для газов, систематизируя разновидности теплоемкостей.

Удельные теплоемкости

Удельная массовая теплоемкость – это количество теплоты, необходимое для нагрева 1 кг газа на один градус. Она обозначается буквой с, имеет единицу измерения Дж/(кгград), определяется как

c = Q/(mdt) = q/dt . (3.17)

Удельная мольная теплоемкость – это количество теплоты, необходимое для нагрева одного моля (киломоля) газа на один градус. Ее обозначение с_, единица измерения Дж/(кмольград), расчетное выражение соответствует произведению молярной массы газа на его удельную массовую теплоемкость, т.к. в одном киломоле содержиться  килограммов газа:

с_ = с , (3.18)

где  – молекулярная масса газа, кг/кмоль.

Удельная объемная теплоемкость газа – это количество теплоты, необходимое для нагрева одного кубического метра газа на один градус. Ее обозначение с', единица измерения Дж/(м³град), расчетное выражение соответствует следующим соотношениям:

c' = Q/(Vdt) = C /V = mQ/(mVdt) =

= m/V(q/dt) = c = c/v = c_/V_ , (3.19)

где  – плотность газа, кг/м³;

v – удельный объем газа, м³/кг;

V_ – объем 1 киломоля газа, м³/кмоль.

Плотность газа и объем одного киломоля газа зависят от температуры и давления, поэтому при различных параметрах объемная теплоемкость одного и того же газа различна даже в случае постоянной ее удельной массовой теплоемкости. Для практического пользования такой теплоемкостью необходимо к каждому ее значению указывать соответствующие ему значения температуры и давления газа, что очень неудобно. В справочной литературе принято давать объемную теплоемкость газа, отнесенную к одному кубическому метру газа, взятому при нормальных физических условиях – 0 ^оС и 760 мм рт.ст. (нм³). При нормальных условиях один киломоль любого идеального газа занимает объем 22,4 м³. При этих условиях удельную объемную теплоемкость идеального газа удобно определять как

с' = с_/22,4 , (3.20)

в единице измерения этой теплоемкости присутствует нормальный кубический метр газа, Дж/(нм³град).