пособие. ТТД ч1 учебное пособие. Техническая термодинамика

• Название: Техническая термодинамика
• Анкор: пособие
• Дата: 02.02.2023
• Размер: 4.15 Mb.
• Имя файла: ТТД ч1 учебное пособие.doc
• Тип: Учебное пособие; #917693
• страница: 7 из 19

Основные характеристики смеси газов

Для того чтобы воспользоваться уравнением Менделеева-Клапейрона для смеси газов

, , ,

необходимо знать газовую постоянную R_см и молярную массу (условную) смеси µ_см. Для смеси, как для любого идеального газа, эти две величины связаны соотношением R_см=8314/µ_см (Дж/(кг·К)). Чтобы рассчитать эти величины, необходимо знать состав смеси газов, т.е. какие газы и в какой пропорции входят в смесь.

Состав смеси может быть задан массовыми, объемными или мольными долями.

Массовой долей g_i данного газа называется отношение его массы к массе всей смеси:

, (3.67)

где m_i – масса отдельного газа, входящего в смесь;

m_см – общая масса смеси.

Очевидно, что сумма массовых долей всех газов смеси равна единице:

. (3.68)

Объeмной долей r_i данного газа называется отношение объема, который занимал бы данный газ при температуре и давлении смеси, к общему объему смеси:

, (3.69)

где V_i – объем данного газа при Т_см и Р_см, м³.

Объем V_i называют парциальным объемом, это искусственно введенная величина, поскольку каждый газ, входящий в смесь, занимает весь объем смеси. Парциальный объем можно рассчитать по уравнению Менделеева – Клапейрона:

. (3.70)

Записав уравнение Менделеева – Клапейрона через парциальное давление и через парциальный объем,

,

,

можно получить еще одно расчетное выражение для объемной доли, поделив правые и левые части этих уравнений одно на другое:

. (3.71)

Поскольку сумма парциальных давлений равна давлению смеси, то сумма объемных долей всех газов смеси равна единице, а сумма парциальных объемов равна полному объему всей смеси газов:

, (3.72)

. (3.73)

Для смеси газов используется понятие мольных долей. Мольной долей называется отношение количества молей данного газа М_i к общему количеству молей всех газов смеси М_см.

Количество молей определяется делением массы газа на его молярную массу:

. (3.74)

Воспользовавшись уравнением Менделеева – Клапейрона для парциального и полного объемов смеси газов и введя в него количество молей

,

,

получим еще одно расчетное выражение для мольной доли:

. (3.75)

Равенство объемных и мольных долей для смеси газов можно получить и из закона Авогадро, в соответствии с которым объемы молей всех идеальных газов при одинаковых параметрах одинаковы, т.е. число молей при одинаковых параметрах идеальных газов прямо пропорционально полным объемам этих газов: V_i=V_i/М_i=V_см/М_см=V_см.

Существует взаимосвязь массовых и объемных долей смеси. Ее несложно получить, выразив массы газов через произведение их объемов на плотности, а отношение плотностей при одинаковых параметрах, в соответствии с законом Авогадро, заменив отношением молекулярных масс:

. (3.76)

Уравнение (3.76) позволяет получить расчетные выражения для молярной массы и газовой постоянной смеси газов на основании равенства единице суммы массовых и объемных долей всех газов данной смеси:

,  ,  , (3.77)

,  ,  . (3.78)

При известной молярной массе смеси газовую постоянную смеси проще определить из соотношения

.

Для определения парциального давления данного газа в смеси можно воспользоваться выражением (3.71). В соответствии с ним

P_i = r_iP_см .
Теплоемкости газовых смесей

Полная теплоемкость смеси газов представляет собой сумму теплоемкостей газов, составляющих смесь. Это справедливо, поскольку теплота подчиняется закону суммирования (адитивности).

. (3.79)

Удельную массовую теплоемкость смеси газов можно получить, разделив выражение (3.79) на массу смеси газов и выразив полные теплоемкости каждого газа через произведение их масс на соответствующие им удельные массовые теплоемкости:



.

Получили, что удельная массовая теплоемкость смеси газов равна сумме произведений массовых долей на удельные массовые теплоемкости газов, составляющих смесь:

. (3.80)

Удельную объемную теплоемкость смеси газов можно получить, разделив выражение (3.79) на объем смеси и выразив полные теплоемкости каждого газа в виде произведения их парциальных объемов на соответствующие им удельные объемные теплоемкости:



.

И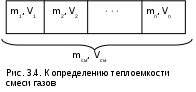
спользование парциальных объемов правомерно (рис.3.4), поскольку они соответствуют массовому количеству каждого газа, входящему в смесь, т.е. количество теплоты можно представить выражением



.

Получили, что удельная объемная теплоемкость смеси газов равна сумме произведений объемных долей на удельные объемные теплоемкости газов, составляющих смесь:

. (3.81)

Удельную мольную теплоемкость смеси газов можно получить, умножив выражение (3.81) на объем одного киломоля, поскольку по закону Авогадро объем одного киломоля всех идеальных газов при одинаковых параметрах одинаков (V_cм=V_1=V_2==V_n):



.

Получили, что удельная мольная теплоемкость смеси газов равна сумме произведений объемных долей на удельные мольные теплоемкости газов, составляющих смесь:

. (3.82)

Для простоты запоминания расчетных выражений характеристик смеси идеальных газов можно воспользоваться следующей закономерностью: все характеристики смеси газов, которые рассчитываются в виде суммы произведений характеристик отдельных газов на их доли, имеют в расчетных выражениях массовые доли, если характеристика в знаменателе имеет единицу измерения массы килограмм (кг), во всех остальных случаях их характеристики умножаются на объемные доли.

Например, единица измерения газовой постоянной смеси R_см (Дж/(кгК)) – она рассчитывается в виде алгебраической суммы произведений газовых постоянных R_i на массовые доли ее компонентов g_i, т.к. в знаменателе ее единицы измерения находится килограмм (кг).
4. ГАЗОВЫЕ ПРОЦЕССЫ

Термодинамическим газовым процессом называется процесс изменения состояния газа, при котором происходит энергетическое взаимодействие газа и окружающей среды в виде теплоты и работы, в результате чего происходит изменение параметров газа.

В термодинамике рассматриваются закономерные процессы. Закономерность процесса может быть выражена закономерным энергетическим взаимодействием газа и окружающей среды. Следствием такого энергетического взаимодействия будет закономерное изменение параметров газа [8].

4.1. Политропные процессы

В переводе на русский язык слово «политропный» означает закономерный. Закономерность энергетических взаимодействий приведет к закономерному изменению членов первого закона термодинамики для данного тела. В случае обратимого (без трения) процесса соблюдается первый закон термодинамики q=du+. Для закономерного процесса имеется определенное соотношение между членами уравнения первого закона термодинамики. Обычно за величину, определяющую закономерность энергетического взаимодействия, принимают отношение изменения внутренней энергии к количеству подведенной теплоты:

 = du/q . (4.1)

Действительно, в случае постоянства =const получается, что все члены первого закона термодинамики будут находиться в строгом соотношении друг с другом, определяемом величиной :

, ,

, . (4.2)

Процессы, подчиняющиеся закономерному энергетическому взаимодействию, при котором  = du/q = const, называются политропными.

Рассмотрим обратимый (без трения) закономерный (политропный) процесс применительно к идеальному газу.

Для идеальных газов с постоянными изобарными и изохорными теплоемкостями политропный процесс будет характеризоваться следующими соотношениями:

du= c_vdT = q = cdT .

Поскольку c_v=const и =const, то и теплоемкость политропного процесса для идеального газа будет величиной постоянной:

c = c_v/ = const . (4.3)

Постоянство теплоемкости определяет закономерность изменения параметров в политропном процессе. Для определения этой закономерности воспользуемся двумя уравнениями первого закона термодинамики:

q=cdT=dh-vdp=c_pdT-vdp;

q=cdT=du+pdv=c_vdT+pdv.

Преобразуем эти уравнения, переместив члены с теплоемкостями в левую часть:

(c-c_p)dT = - vdp,

(c-c_v)dT = pdv .

После деления правых и левых частей равенств друг на друга получим постоянную величину

. (4.4)

Обозначим левую часть равенства буквой n:

. (4.5)

Эта постоянная величина n получила название показателя политропы.

Подставив показатель политропы в выражение (4.4) и сделав элементарные преобразования, получим соотношение

npdv = - vdp или npdv + vdp = 0 .

Разделив последнее равенство на произведение pv, получим

ndv/v + dP/P = 0 .

После интегрирования последнего равенства получаем



или окончательно

Рvⁿ = const . (4.6)

Уравнение (4.6) называется уравнением политропы. Оно описывает закономерность изменения параметров в политропном процессе. В выражении (4.6) дана взаимосвязь двух термических параметров P и v. Поскольку состояние идеального газа подчиняется уравнению Pv=RT, то, выразив Р и v через соответствующую пару термических параметров v, Т и Р, Т и подставив их поочередно в выражение (4.6), получим уравнения политропы, описывающие взаимосвязь параметров v, Т и Р, Т:

; (4.7)

. (4.8)

Политропа в системе координат P-v-T представляет собой кривую, проекции которой на оси P-v, T-v, T-P описываются уравнениями (4.6), (4.7), (4.8). Константы этих уравнений определяются по любой паре термических параметров для одной из точек (любой), находящейся на этой политропе. Таким образом, политропа считается заданной, если известны ее параметры хотя бы в одной точке и задан показатель политропы n.

П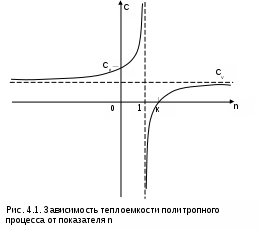
ри одинаковых показателях политропы n константы в выражениях (4.6), (4.7), (4.8) для различных политроп будут иметь различные значения. Такие политропы имеют одинаковую закономерность изменения параметров и в системе координат термических параметров состояния не пересекаются.

Расчетное выражение для теплоемкости политропного процесса получается из уравнения (4.5):

, ,

. (4.9)

Показатель политропы может иметь численные значения от - до +. В соответствии с уравнением (4.9) теплоемкость политропных процессов в зависимости от n также может принимать значения от - до +. Функциональная зависимость теплоемкости политропного процесса от n приведена на рис.4.1.

Используя уравнение (4.9), получим расчетное выражение для константы  в политропном процессе:

. (4.10)

В политропном процессе при изменении параметров идеального газа от точки 1 до точки 2 изменение внутренней энергии, энтальпии и энтропии определяется по уравнениям

u₂ - u₁ = c_v(T₂ - T₁); (4.11)

h₂ - h₁ = c_p(T₂ - T₁); (4.12)

. (4.13)

Изменение энтропии можно рассчитать по изменению любого термического параметра, а не только по изменению температуры. Для этого достоточно воспользоваться уравнениями (4.7) и (4.8):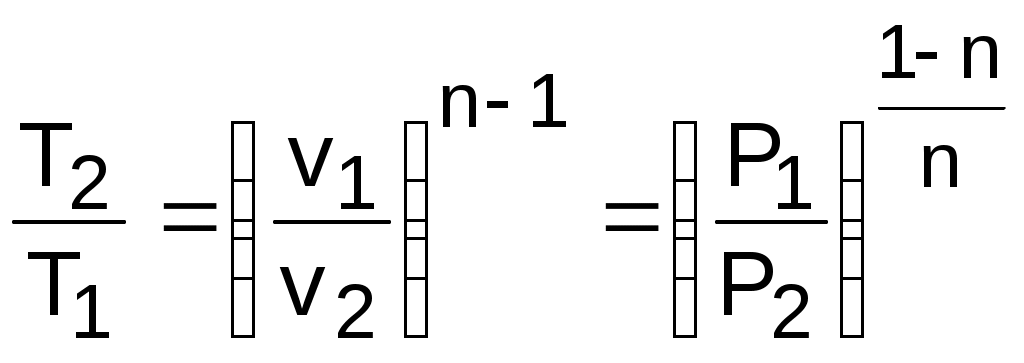

. (4.14)

Расчет теплоты в политропном процессе целесообразно вести по следующей зависимости:

. (4.15)

Работа в политропном процессе может быть определена как ин­теграл или из первого закона термодинамики:



. (4.16)

Используя выражение (4.16), можно определить работу, зная изменение любого параметра. Для этого отношение температур необходимо выразить через отношение объемов или давлений в соответствии с выражениями (4.14).