пособие. ТТД ч1 учебное пособие. Техническая термодинамика
 Скачать 4.15 Mb. Скачать 4.15 Mb.
|
1.3.2. Уравнение состояния термодинамической системыВсе термодинамические параметры гомогенной сисемы (однородной – с одинаковыми физическими свойствами), находящейся в равновесном состоянии, имеют определенную функциональную связь. При отсутствии действия внешних полей термодинамически равновесное состояние любого однородного реального тела определяется всего лишь двумя независимыми параметрами. Для неоднородных систем могут два параметра взаимно определять друг друга (например, давление и температура влажного насыщенного пара), в этом случае необходим третий параметр. В качестве независимых параметров могут быть выбраны: давление и температура, давление и удельный объём или любая пара независимых свойств (температура и энтропия, давление и энтальпия и т.п.). При заданных значениях двух параметров термодинмически равновесной системы можно определить любые другие ее параметры. Связь между параметрами такой системы описывается уравнениями состояния. Например, связь между параметрами p, v, T может быть выражена термическими уравнениями состояния системы: - в неявной форме f(p,v,T) = 0 , (1.12) - в явной форме p = F(v,T); v = f(p,T); T = j(p,v). (1.13) В системе координат P,v,T эти уравнения описывают поверхность, называемую термодинамической (рис. 1.8). В  ид функциональной зависимости между параметрами различен для различных веществ и может быть получен либо из опыта, либо на базе микрофизических теорий. Методами самой термодинамики эта связь определена быть не может. 1.3.3. Термические коэффициентыВзаимосвязь свойств однородного вещества в равновесном состоянии может также характеризоваться термическими коэффициентами. Эти коэффициенты могут быть определены опытным путем, они имеют определенный физический смысл. Взаимосвязь термических коэффициентов можно получить, используя уравнение состояния вещества в явном виде Р=F(v,T), представив его как полный дифференциал приняв Р = const, получим преобразовав это выражение, получим соотношение вида 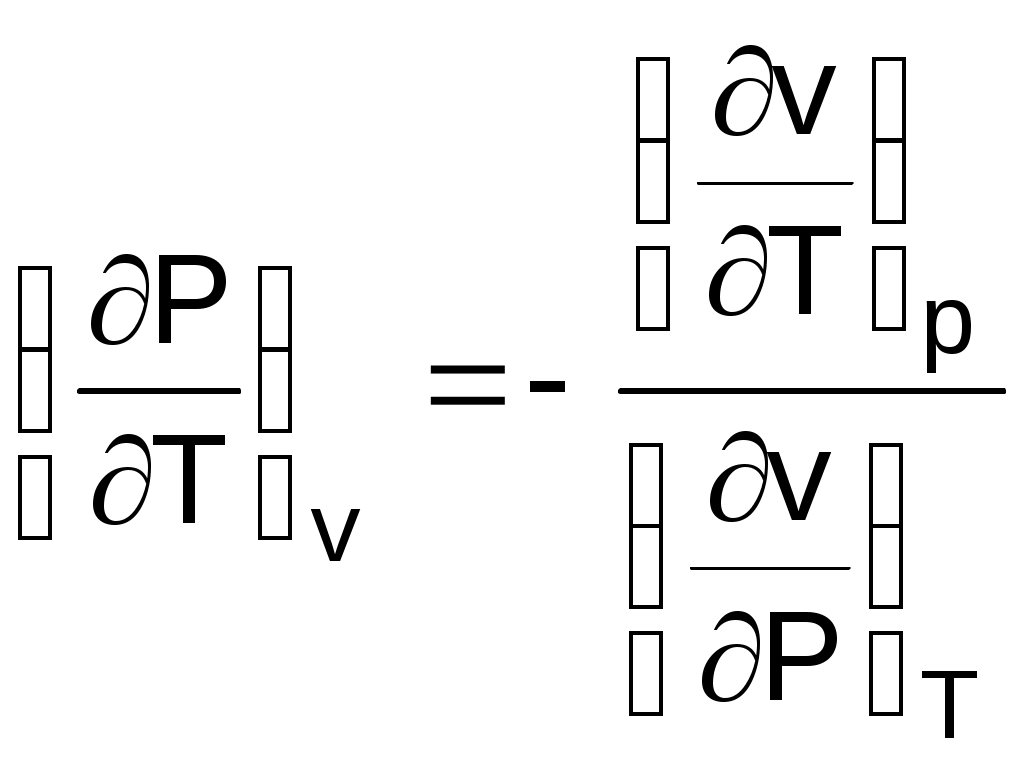 . (1.15) . (1.15)В выражении (1.15) отношение (dv/dP)T характеризует интенсивность изменения объема в зависимости от изменения давления при постоянной температуре. Отношение этой величины к удельному объему vo, взятому при фиксированном состоянии (например, при нормальных условиях) с обратным знаком, называется коэффициентом изотермическойсжимаемости и обозначается как : Отношение (dv/dТ)Р характеризует интенсивность изменения объема в зависимости от изменения температуры при постоянном давлении. Разделив его на vо, получим коэффициент изобарного расширения, обозначающийся как : Отношение (dР/dТ)v характеризует изменение давления в зависимости от изменения температуры при постоянном объеме. Разделив его на Ро, получим коэффициент упругости, обозначающийся как : Выразив значения частных производных в выражении (1.15) через термические коэффициенты (dv/dP)T=-vo , (dv/dТ)P=vo , (dР/dТ)v=Po и подставив их в (1.15), получим уравнение взаимосвязи термических коэффициентов: Выражение (1.19), как и уравнение состояния, описывает свойства вещества. Кроме этого, выражение (1.19) необходимо для расчета коэффициента твердых и жидких тел, поскольку эти тела невозможно нагреть без изменения их объема, т.е. для них опытным путем определить невозможно. 1.3.4. Термодинамический процесс Понятие термодинамического процесса характеризует термодинамическую систему с точки зрения ее энергетического взаимодействия с окружающей средой. Термодинамическим процессомназывается процесс изменения состояния термодинамического тела (системы), не находящегося в термодинамическом равновесии с внешней средой и не изолированного от нее. При этом наблюдается энергетическое взаимодействие между телом и окружающей средой, сопровождающееся изменением параметров тела. Строго говоря, только для процессов, происходящих очень медленно, с малыми отклонениями промежуточных параметров (квазистатические равновесные процессы), можно воспользоваться уравнениями состояния, а сам процесс геометрически представить в виде непрерывной кривой на термодинамической поверхности. Графическое изображение действительных неравновесных процессов, протекающих с конечной скоростью, имеет условный характер. Понятие равновесности характеризует поведение параметров внутри и на границах тел при процессах, но не затрагивает превращения форм энергии и распределения ее в системе. Для характеристики процессов с точки зрения превращения и распределения энергии между всеми телами, участвующими в процессе, вводится понятие обратимости процессов. Обратимыми называются процессы, которые могут быть проведены в прямом и обратном направлениях таким образом, что все тела, участвующие в процессе, проходят через одни и те же промежуточные равновесные состояния (но в обратной последовательности), а после проведения прямого и обратного процессов все тела закрытой изолированной системы возвращаются в первоначальное состояние, и, следовательно, распределение энергии между ними оказывается прежним. Процессы, не отвечающие поставленным условиям, называются необратимыми. Все неравновесные процессы необратимы. Так, при неравенстве давления в рабочем теле и внешнего давления рабочее тело расширяется или сжимается, в результате возникают вихревые движения, которые со временем успокаиваются, а их энергия переходит в энергию теплового движения частиц. В этом случае наблюдается переход механической работы в теплоту, в результате чего для возврата системы в первоначальное состояние потребуется дополнительное количество механической работы. При отсутствии термического равновесия процесс также необратим. Теплота самопроизвольно переходит от тела более нагретого к телу менее нагретому, и обратный переход теплоты возможен только при наличии дополнительного источника теплоты. Необратимость процессов подразделяется: - на внешнюю необратимость, вызванную разностью температур при теплообмене между телами; - внутреннюю необратимость, вызванную наличием трения. В прямом и обратном процессах в этом случае имеется работа, затрачиваемая на трение, она превращается в теплоту. Всякая необратимость связана с уменьшением возможной работы системы, эта потеря является мерой необратимости процесса. Процессы с полной потерей возможной работы называются предельно необратимыми. Примерами предельно необратимых процессов могут служить: расширение газа в вакуум, дросселирование газов и паров, рассеяние теплоты горячего тела в окружающую среду и т.п. При термодинамических исследованиях процессов обычно не касаются внешней необратимости, обусловленной разностью температур при теплообмене, сами же процессы принимаются (естественно условно) внутренне равновесными. Такие процессы легко поддаются термодинамическому анализу, так как они могут изображаться графически в виде сплошных линий на диаграммах параметров состояния. Пример обратимого и необратимого процессов с их графическим изображением в P,V- диаграмме приведен на рисунке 1.9. Для обратимого процесса (рис. 1.9, а) сжатия газа в цилиндре с поршнем 1а2 характерно отсутствие трения (при этом под трением понимаем не только трение от взаимодействия поршня со стенками цилиндра, но и трение взаимодействия самого газа со стенками цилиндра и поршнем). На совершение процесса 1а2 затрачивается механическая работа L, соответствующая площади под процессом в P,V- диаграмме (в дальнейшем это будет доказано). Если дать возможность газу расшириться до первоначального состояния тоже по обратимому процессу 2а1, он повторит траекторию процесса 1а2 в обратной последовательности и вернется в первоначальное состояние 1. При этом механическая работа процесса расширения 2а1 будет численно равна механической работе сжатия процесса 1а2, но знак ее будет противоположный (-L). В результате осуществления прямого 1а2 и обратного 2а1 процессов суммарная внешняя механическая работа будет равна нулю: L=0, т.е. распределение энергии в системе остается неи 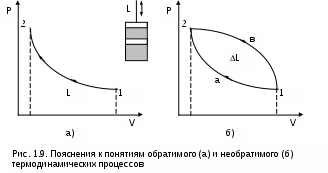 зменным, а процесс 1а2 по определению обратимый. В необратимом процессе (рис. 1.9, б) сжатия газа в цилиндре 1а2 часть работы затратится на преодоление трения. Поэтому для возвращения газа в первоначальное состояние даже по обратимому процессу расширения работы сжатого газа будет недостаточно и потребуется дополнительная внешняя механическая работа. Следовательно, траектория обратного процесса 2в1 пройдет выше, чем у процесса 2а1. Разница работ этих процессов L соответствует площади 1а2в1 в Р,V- диаграмме. Она отлична от нуля (L>0), т.е. распределение энергии при возврате системы в первоначальное состояние изменилось, а процесс 1а2 по определению необратимый. Все действительные процессы необратимы. В тех случаях, когда необратимость значительно изменяет характер процесса, это необходимо учитывать. 2. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ ДЛЯ ЗАКРЫТОЙ СИСТЕМЫ Первый закон термодинамики является одним из двух основных законов, на которых базируется вся современная термодинамика. Он получен на основании наблюдений и не имеет никакого другого доказательства, кроме человеческого опыта в земных условиях. Открытие первого закона термодинамики относится к середине XIX века, а его основоположниками считают Р.Майера и Д.Джоуля [1]. Известно, что процесс изменения состояния термодинамического тела (системы) происходит при энергетическом взаимодействии его с внешней средой. Мерой этого взаимодействия является работа. Первый закон термодинамики представляет собой приложение к термодинамической системе общего закона сохранения энергии, согласно которому в замкнутой изолированной системе возможны взаимопревращения форм энергии, но сумма всех видов энергии является величиной постоянной. Аналитическое выражение этой формулировки будет соответствовать равенству энергии такой термодинамической системы в начале и конце процесса: ΔE=0 или Е=const, (2.1) где Е – энергия термодинамической системы. Для неизолированной термодинамической системы изменению энергии будет соответствовать сумма работ, произведенных в этой системе, поскольку работа есть мера энергетического взаимодействия. Для такой системы закон сохранения энергии будет представлен выражением ΔЕ = А1 + А2 + А3 + ··· + Аn , (2.2) где А1 … Аn – работы данной термодинамической системы. Для получения выражения первого закона термодинамики необходимо установить взаимосвязь различных форм преобразования энергии с полученными в результате этих преобразований работами в теле или системе. В данном разделе познакомимся с первым законом термодинамики для закрытых (без обмена веществом с окружающей средой) термодинамических систем. Для открытых систем первый закон термодинамики будет рассмотрен позднее, по мере необходимости изучения соответствующих процессов: истечения, дросселирования, смешения и т.п. Для строгого математического формулирования этого закона необходимо дать понятия возможных форм энергии и работ, применительно к термодинамической системе. 2.1. Работа изменения объема Работа изменения объема есть мера механического энергетического взаимодействия тела и внешней среды, являющаяся результатом изменения объема тела. Иногда эту работу называют работой расширения, хотя тело в результате этого энергетического взаимодействия может как увеличивать, так и уменьшать свой объем. Применяя формулу элементарной работы в механике (2.3) к классической модели термодинамики – цилиндр с газом и поршнем (рис. 2.1), получим аналитическое выражение работы изменения объема: 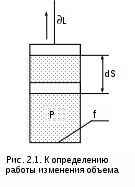 L = FsdS , (2.3) L = FsdS , (2.3)где L – элементарная работа (обозначает бесконечно малую неполного дифференциала); Fs – проекция силы на направление движения; dS – элементарное перемещение. Силовое воздействие нагруженного поршня в состоянии равновесия уравновешивается силовым воздействием газа: F = Fs = Рf, (2.4) где P – давление газа; f – площадь поршня. При увеличении объема газа на величину dV поршень переместится на расстояние dS = dV/f. (2.5) Следовательно, газом совершается работа по перемещению поршня (Дж) L = FsdS = РfdV/f = РdV, (2.6) которая и называется работой изменения объема. При отсутствии трения эта работа равняется внешней работе, т.е. работе газа над внешней средой. При наличии трения внешняя работа L' меньше работы L на величину работы трения, т.е. L'=L-Lтр. Для одного килограмма газа элементарная работа, которая называется удельной работой изменения объема, выразится равенством (Дж/кг) = L/m = РdV/m = Рdv, (2.7) где m – масса газа, кг. Выражение (2.7) применимо к телу любой конфигурации. Полную работу расширения при конечном изменении объема газа можно вычислить интегрированием выражения (2.7), если есть функциональная зависимость давления от объема: О 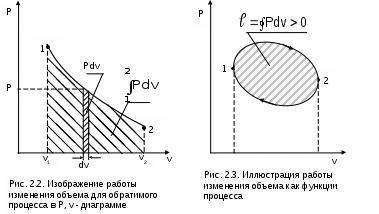 на соответствует площади под процессом в проекции на ось v в P,v- диаграмме (рис. 2.2). Поэтому P,v- диаграмму называют рабочей диаграммой. Выражения (2.6) и (2.7) справедливы для обратимого термодинамического процесса. Знак неполного дифференциала () в этих выражениях указывает на то, что работа расширения есть функция процесса. Она зависит от характера процесса, а ее интеграл по замкнутому контуру – работа кругового процесса (цикла) – не равен нулю (рис. 2.3) в отличие от полного дифференциала любого из параметров состояния (например, В технической термодинамике принято, что работа изменения объема положительна, когда тело совершает работу над внешней средой при увеличении его объема (dv>0), и отрицательна, когда внешняя среда совершает работу над телом при уменьшении его объема (dv<0). Основной единицей работы изменения объема является джоуль (Дж). Работа, отнесенная к одному килограмму вещества, 2.2. Теплота, теплоемкость, энтропия П 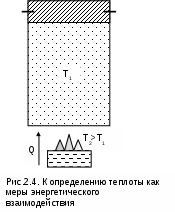 усть в цилиндре под поршнем (рис. 2.4) находится газовое термодинамическое тело. Закрепив поршень штифтами, исключим возможность механического взаимодействия тела с окружающей средой. Также исключим химическое, ядерное, электрическое и прочие взаимодействия тела с окружающей средой, оставив возможность только теплового энергетического взаимодействия. В результате теплового энергетического взаимодействия, которое обусловлено наличием разных температур у данного газа и окружающей среды, будет наблюдаться изменение температуры тела (в данном случае увеличение), т.е. энергия газа изменилась. Мерой любого энергетического взаимодействия является работа. Назовем работу данного примера тепловой работой, или, как принято говорить, теплотой. усть в цилиндре под поршнем (рис. 2.4) находится газовое термодинамическое тело. Закрепив поршень штифтами, исключим возможность механического взаимодействия тела с окружающей средой. Также исключим химическое, ядерное, электрическое и прочие взаимодействия тела с окружающей средой, оставив возможность только теплового энергетического взаимодействия. В результате теплового энергетического взаимодействия, которое обусловлено наличием разных температур у данного газа и окружающей среды, будет наблюдаться изменение температуры тела (в данном случае увеличение), т.е. энергия газа изменилась. Мерой любого энергетического взаимодействия является работа. Назовем работу данного примера тепловой работой, или, как принято говорить, теплотой.Теплота, или тепловая работа, – мера теплового энергетического взаимодействия тел. Она обусловлена при наличием разности температур между телами. Теплота имеет обозначения Q и q=Q/m – удельная теплота. Их единицы измерения такие же, как и у работы изменения объема (Дж) и (Дж/кг), поскольку природа их одинакова – мера энергетического взаимодействия. Если система состоит из нескольких тел, то ее теплота равна сумме теплот, подведенных к каждому телу. Она подчиняется закону суммирования, или аддитивности, как говорят математики. Количество передаваемой теплоты научились определять довольно точно в XYIII – XIX веках в результате развития калориметрии. Поскольку подвод или отвод теплоты связан, как правило, с изменением температуры тела, то первоначально и была установлена опытным путем эта взаимосвязь в виде выражения Q = CdT, (2.9) где Q – теплота; C – коэффициент пропорциональности, названный теплоемкостью. Теплоемкость есть количество теплоты, необходимое для нагрева тела на один градус (Дж/град): C =Q/dT . (2.10) Теплоемкость так же, как и теплота, обладает аддитивностью (свойством суммирования в зависимости от количества вещества). Отнесенная к одному килограмму массы вещества она называется удельной массовой теплоемкостью (Дж/(кг град)): с = Q/(mdT) = q/dT, (2.11) где q – удельная теплота. Так же как и любая другая работа, теплота есть функция процесса, о чем и свидетельствует знак неполного дифференциала . Следовательно, и теплоемкость есть функция процесса. На практике широко используются удельные теплоемкости для процессов при постоянном давлении cp – изобарная теплоемкость – и постоянном объеме cv – изохорная теплоемкость. Необходимо отметить, что теплоемкость реальных веществ – величина переменная. Она зависит от давления и от температуры вещества. Подробное изложение материала о теплоемкостях будет приведено в гл. 4 и 6. Вернемся к теплоте. Полное ее количество с использованием теплоемкости данного процесса определяется интегрированием выражения (2.9) или (2.11). 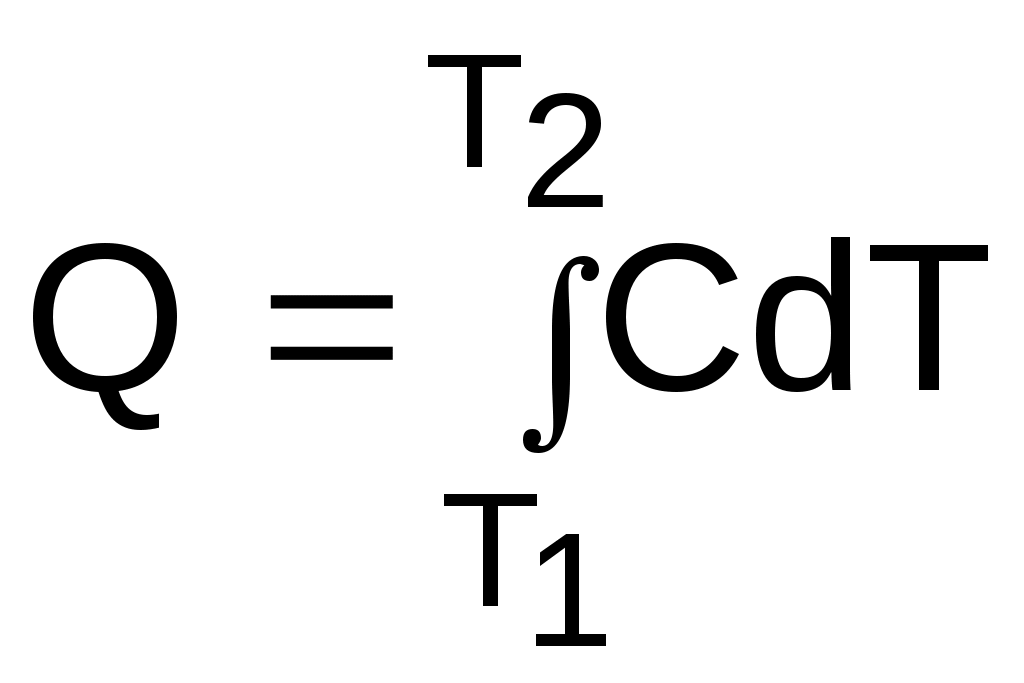 , (2.12) , (2.12)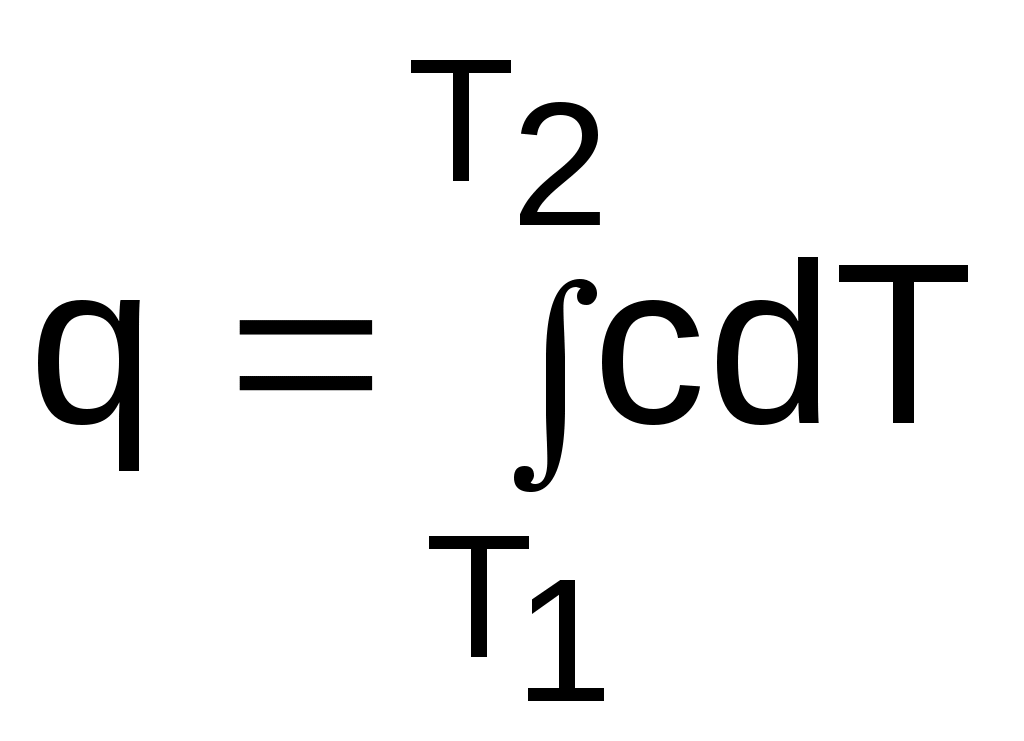 , (2.13) , (2.13)где С и с – полная и удельная массовая теплоемкости; Q и q – полная и удельная теплоты. Отметим, что разница температур в градусах Кельвина и Цельсия одинакова, то есть dT = d(273,15 + t) = dt. (2.14) Поэтому единицы измерения теплоемкостей и расчетные формулы теплоты могут иметь обозначения изменения температуры как в градусах Кельвина (Дж/(кг·К)) так и Цельсия (Дж/(кг·оС)): q = cdT = cdt, (2.15) с = q/dT = q/dt . (2.16) С помощью теплоемкости не всегда возможно рассчитать теплоту. Так при фазовых переходах вещества температура тела не изменяется (Т=const), но теплота фазового перехода не равна нулю (q0). Например, при постоянном атмосферном давлении плавление льда требует подвода теплоты, при этом температура жидкой и твердой фаз воды остается неизменной и равной 0 оС. В этом случае воспользоваться выражением (2.14) для определения теплоты нельзя, т.к. dt = 0, а c = . Кроме того, природа теплоты та же, что и природа любой работы – мера энергетического взаимодействия. Следовательно, теплота может быть рассчитана по формуле обобщенной работы как произведение некоторой силы Fx на изменение некоторой координаты перемещения dx в направлении действия данной силы: A = Fxdx . (2.17) Сила и координата перемещения должны являться функциями состояния – параметрами (аналогично Р и v для работы изменения объема =Pdv). При этом сила должна быть интенсивным параметром, а координата перемещения экстенсивным параметром состояния. Ни теплоемкость, ни изменение температуры в выражении (2.14) этим условиям не соответствуют. В 1865 г. Клиузиусом [1] было предложено понятие энтропии (в переводе с греческого – превращение), соответствующее выражению dS = Q/T . (2.18) Используя энтропию, можно получить расчетное выражение теплоты в виде Q = TdS . (2.19) Выражение (2.19) отвечает расчетному выражению теплоты как работы. При этом абсолютная температура Т и энтропия S являются параметрами состояния: Т – интенсивный параметр, S – экстенсивный. Абсолютная температура в выражении (2.19) выступает в роли силы, а энтропия в роли координаты перемещения под действием этой силы при совершении тепловой работы или теплоты. Исходя из вышеизложенного, дадим определение энтропии применительно к технической термодинамике. Энтропия – параметр состояния, соответствующий координате перемещения при действующей силе в виде абсолютной температуры, необходимый для расчета тепловой работы (теплоты). Принадлежность энтропии к параметрам состояния будет доказана в гл; 4, 6, 8. В этих главах также будет дана и методика определения численных значений энтропии идеальных газов и реальных веществ. В технической термодинамике понятие энтропии неразрывно связано с понятием теплоты: есть теплота – есть изменение энтропии, нет теплоты – нет изменения энтропии. В статистической термодинамике [4] энтропия выступает в другой роли – вероятностной оценки состояния термодинамической системы. В разделе математики "Теория вероятности" также пользуются понятием энтропии. Математики используют название энтропии для вероятностой оценки событий по аналогии со статистической термодинамикой, но в математике это понятие никакого отношения к теплоте не имеет. В дальнейшем, при изучении второго закона термодинамики, понятие энтропии будет иметь более широкое значение. Необходимо отметить, что значение имеет только изменение энтропии, абсолютная величина энтропии никакой физической сути не имеет. Поскольку энтропия – параметр состояния, она может быть определена любой парой независимых параметров состояния. Энтропия подчиняется закону сложения. Энтропия в расчете на один килограмм вещества называется удельной энтропией (Дж/(кг·К)): ds = Q/(mT) = q/T . (2.20) Изменение энтропии однозначно определяет знак теплоты. При увеличении энтропии (ds > 0) теплота подводится к системе (q > 0), при уменьшении энтропии (ds < 0) теплота отводится (q < 0). Используя понятие энтропии, теплоту легко графически показать в T,s- координатах (рис. 2.5). Для построения оси энтропий s в этом случае выбирают начало отсчета, соответствующее фиксированному состоянию вещества (любая пара независимых параметров состояния). Часто в качестве начала отсчета энтропии берется нормальное физическое состояние – 0 оС и 760 мм рт.ст. При этих значениях принимают, что sо = 0, тогда разность энтропий будет иметь численное значение, равное абсолютной величине энтропии (s=s-sо), которое может быть подсчитано для данного вещества на базе выражения (2.20), путем его интегрирования от нулевого до данного состояния вещества. Причем путь интегрирования никакой роли не играет, поскольку энтропия есть параметр состояния. На рис. 2.5 в виде линии 12 представлен процесс изменения состояния термодинамического тела. Заштрихованная площадка под элементарным участком процесса равняется произведению Tds и представляет элементарное количество теплоты q. Интегральная сумма таких площадок под линией 12 представляет полное количество теплоты, получаемое телом в процессе 12. 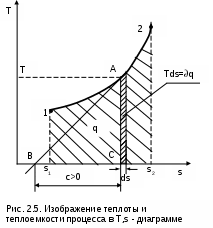 . (1.21) . (1.21)Так как площадь под кривой процесса в T,s- диаграмме соответствует количеству теплоты, она получила название тепловой диаграммы аналогично Р,v- диаграмме, называемой рабочей. В T,s- диаграмме можно графически показать теплоемкость в любой точке процесса. Например, для точки А теплоемкость будет в виде отрезка ВС, образованного касательной к точке А – АВ и проекцией точки А на ось энтропий – АС: с = ВС = TBC/AB = Tds/dT = q/dT . (1.22) Отрезок ВС носит название подкасательной. При этом теплоемкость положительна, если подкасательная расположена слева от точки (А), и отрицательная, если справа. 2.3. Внутренняя энергия Любая термодинамическая система обладает запасом энергии. Суммарная энергия системы складывается из суммы энергий различных видов, присущих соответствующим формам движения материи: тепловой, химической, ядерной и др. Понятие энергии неисчерпаемо как в макромир, так и в микромир. В дальнейшем будем рассматривать замкнутую термодинамическую систему, неподвижную относительно поверхности Земли и без учета сил ее гравитационного взаимодействия с Землей. Энергию такой термодинамической системы назовем внутренней энергией. Термодинамика не занимается общим запасом внутренней энергии тела, она имеет дело с изменением внутренней энергии тела (системы) при различных процессах механического и теплового энергетического взаимодействия тела и окружающей среды. При этом интерес представляет только изменяющаяся часть внутренней энергии тела или системы. Поэтому для расчета абсолютного значения внутренней энергии в термодинамике принимают условное ее нулевое значение при определенном фиксированном состоянии тела или системы. Относительно этого состояния ведется определение внутренней энергии тела (системы). При такой условности в расчетах может получиться, что внутренняя энергия тела будет иметь отрицательный знак. Однако это не значит, что внутренняя энергия тела отрицательная, просто эта энергия находится ниже выбранного уровня ее отсчета. В технической термодинамике рассматриваются процессы, происходящие в макросистемах (на уровне молекул), при отсутствии химических, ядерных, электрических, аннигиляционных и других явлений. Поэтому в термодинамике к внутренней энергии тела (системы) относятся кинетическая энергия беспорядочного теплового движения его молекул, потенциальная энергия связи этих молекул и энергия колебания атомов в них. Потенциальная составляющая внутренней энергии обусловливается работой дисгрегации – разъединения, идущей на увеличение (уменьшение) расстояния между молекулами, т.е. на совершение работы по преодолению сил их взаимного притяжения (отталкивания). Условно внутреннюю энергию можно представить в виде суммы двух слагаемых: U = K + P, (2.23) где U – внутренняя энергия тела (системы); K – кинетическая составляющая внутренней энергии, обусловленная движением микрочастиц; P – потенциальная составляющая внутренней энергии, обусловленная наличием сил взаимодействия (притяжения или отталкивания) между микрочастицами. Внутренняя энергия имеет единицу измерения джоуль (Дж). Она подчиняется закону сложения – аддитивная величина, обладающая экстенсивными свойствами, т.е. для сложной системы, состоящей из нескольких однородных тел, внутренняя энергия будет равна сумме внутренних энергий этих тел: U = U1 + U2 + U3 + ∙∙∙ + Un . (2.24) Для гомогенного (однородного) тела, разделив его внутреннюю энергию на массу тела, получим удельную внутреннюю энергию с единицей измерения джоуль на килограмм (Дж/кг), которая будет обладать интенсивными свойствами: u = U/m . (2.25) Кинетическая составляющая внутренней энергии находится в прямой зависимости от температуры тела, а потенциальная составляющая внутренней энергии тела зависит от расстояния между молекулами, т.е. от плотности или удельного объема вещества. Таким образом, внутренняя энергия оказывается функцией состояния вещества и сама является параметром состояния. Удельная внутренняя энергия однородного тела может быть определена любой парой независимых параметров состояния: u = f(Т,v); u = F(Т,P); u = f(P,v). (2.26) 2.4. Первый закон термодинамики для закрытой системы В технической термодинамике в основном рассматривают процессы изменения состояния термодинамического тела, находящегося только в тепловом и механическом взаимодействии с телами внешней среды. Ранее мы условились, что все процессы будем рассматривать применительно к закрытым термодинамическим системам (без обмена веществом с окружающей средой). Если термодинамическое тело (система) находится в покое или скорость его движения не меняется, т.е. не меняется его кинетическая энергия видимого движения, а также не меняется положение его центра тяжести по отношению к центру Земли, т.е. не меняется его потенциальная энергия в гравитационном поле Земли, то нет изменения запаса его механической энергии. Результатом его взаимодействия с внешней средой в этом случае является изменение его внутренней энергии. Внутренняя энергия может быть изменена за счет подвода (отвода) к телу теплоты (совершения тепловой работы) и за счет совершения над ним со стороны окружающей среды (или самим телом над окружающей средой) работы изменения объема (механической работы). И то и другое является мерой энергетического взаимодействая тела и внешней среды, мерой передачи телу энергии от внешних источников. Согласно закону сохранения энергии в этой системе изменение ее внутренней энергии будет равно сумме внешних тепловых и механических работ. Таким образом, аналитическое выражение первого закона термодинамики для замкнутой системы будет иметь следующий вид: U2 - U1 = Q - L', (2.27) где U2 - U1 – изменение внутренней энергии системы; Q – количество теплоты, полученное телом (системой) от внешней среды; L' – работа расширения, совершаемая телом (системой) над внешней средой. Штрих указывает на то, что это работа расширения действительного необратимого процесса. Подробное изложение различия работ расширения в обратимых и в необратимых процессах будет приведено в следующем разделе. В выражении (2.27) знак минус перед работой изменения объема обусловлен правилом знаков, согласно которому принято, что увеличение внутренней энергии тела (U2-U1>0) возможно за счет подводa к нему теплоты (Q имеет знак «плюс» согласно расчетному выражению dQ=TdS при подводе к телу теплоты (dS>0 и Q>0)) и за счет совершения над ним работы изменения объема со стороны внешней среды (L' – работа изменения объема самого тела, -L' – работа изменения объема внешней среды над телом согласно расчетному выражению для работы изменения объема обратимого процесса dL=PdV при совершении механической работы над телом со стороны окружающей среды (dV<0 и L<0), т.е. в этом случае -L>0). Очевидно, что изменение внутренней энергии может быть вызвано энергетическим взаимодействием тела с окружающей средой одного вида: или только механического, или только теплового. Из выражения (2.27) следует принцип эквивалентности работы расширения (механической работы) и теплоты (тепловой работы), т.е. одинаковость их природы, а соответственно и их единиц измерения. Вот некоторые из часто встречающихся соотношений: 1 ккал = 4,187 кДж; 1 кВт∙ч = 3600 кДж = 860 ккал. |
