пособие. ТТД ч1 учебное пособие. Техническая термодинамика

• Название: Техническая термодинамика
• Анкор: пособие
• Дата: 02.02.2023
• Размер: 4.15 Mb.
• Имя файла: ТТД ч1 учебное пособие.doc
• Тип: Учебное пособие; #917693
• страница: 17 из 19

Среднетермодинамической температурой Т_m называется частное от деления теплоты процесса на изменение его энтропии:

. (8.9)

В диаграмме Т,s- значению Т_m (рис.8.7) соответствует высота прямоугольника авсd, равновеликого площади 12сd.

Используя понятие среднетермодинамической температуры, представим в виде эквивалентного цикла Карно произвольный обратимый цикл 1234 (рис.8.8). Для этого процесс подвода теплоты в цикл 12 заменим изотермическим процессом ав со среднетермодинамической температурой T_1m, а процесс отвода теплоты 34 заменим изотермическим процессом cd со среднетермодинамической температурой T_2m. Полученный цикл Карно авсd имеет q₁ и q₂ равные подведенной и отведенной теплоте рассматриваемого цикла 1234, т.е. это эквивалентные циклы, для которых термический КПД определяется по формуле

.

В
дальнейшем понятие эквивалентного цикла Карно будет использоваться для сопоставления тепловой экономичности различных циклов теплоэнергетических установок.
8.1.3. Обратный цикл Карно

Цикл Карно с протеканием процессов против часовой стрелки называется обратным. Это цикл холодильных машин и тепловых насосов.

Для наглядности сравнения различных типов цикла Карно на рис.8.9 в диаграмме Т,s- представлены: а) цикл двигателя, б) цикл холодильной машины, в) цикл теплового насоса. Для всех циклов окружающая среда выступает в зависимости от их назначения в виде горячего или холодного источника теплоты с температурой Т_ос.

В отличие от цикла двигателя (рис.8.9,а), где окружающая среда выступает в качестве холодного источника теплоты, в цикле Карно холодильной машины (рис.8.9,б) окружающая среда является горячим источником теплоты.

В холодильной установке осуществляется обратный цикл Карно, в котором рабочее тело забирает теплоту q₂ от охлаждаемого тела с температурой Т_х и отдает теплоту q₁ в окружающую среду с температурой Т_оc > T_х. Для осуществления передачи теплоты от холодного тела к теплому затрачивается работа _t, которая, преобразуясь в теплоту q₁=_t+q₂, вместе с q₂ передается окружающей среде. При заданных температурах охлаждаемого тела и окружающей среды обратный цикл Карно будет самым экономичным циклом холодильной установки. Его холодильный коэффициент определяется только температурами Т_оc и T_х и рассчитывается как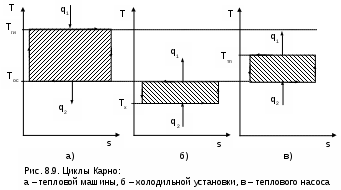


. (8.10)

В тепловом насосе тоже осуществляется обратный цикл Карно (рис.8.9,в), но в этом цикле окружающая среда выступает в роли холодного источника теплоты. При работе теплового насоса теплота внешней среды (т.е. отсутствует сжигание топлива и т.п.) q₂ за счет совершения работы _t передается потребителю теплоты с температурой Т_тп>Т_ос, при этом работа _t преобразуется в теплоту и общее количество теплоты, полученное потребителем, будет представлено величиной q₁=_t+q₂. Коэффициент преобразования теплоты, характеризующий эффективность цикла Карно теплового насоса, определяется только температурами Т_ос и Т_тп, и рассчитывается как

. (8.11)

Холодильный коэффициент (8.10) и коэффициент преобразования теплоты (8.11) в циклах Карно при заданной температуре окружающей среды Т_ос возрастают при увеличении Т_х и уменьшении Т_тп.

Обратимые циклы Карно холодильной машины и теплового насоса при постоянных температурах источников теплоты Т_оc и T_х или Т_ос и Т_тп имеют наибольшую экономичность по сравнению с другими циклами с такими же источниками теплоты.

Анализируя обратный цикл Карно, можно привести следующие формулировки второго закона термодинамики:

передать теплоту от холодного тела к горячему возможно только при затрате работы или другого компенсационного процесса;

самопроизвольный переход теплоты от холодного тела к горячему невозможен.

Осуществить на практике обратимый цикл Карно невозможно, поскольку в природе не существует обратимых процессов, но он является эталоном экономичности, к которому должны стремиться реальные циклы с изотермическими источниками теплоты. Поскольку большинство реальных циклов имеют источники теплоты с переменной температурой, то для получения этквивалентного цикла Карно при таких источниках теплоты пользуются понятием среднетермодинамической температуры и сравнивают его с эталонным циклом Карно (см. разд. 8.1.2).
8.1.4. Регенеративный (обобщенный) цикл Карно

Оказывается, что не только у цикла Карно термический КПД определяется температурами горячего и холодного источников теплоты. Имеется множество обратимых циклов с изотермическими источниками теплоты, для которых термический КПД будет таким же, как и у цикла Карно. Для таких циклов процессы перехода с одной изотермы на другую должны быть эквидистантными, при этом рабочее тело на процессе с уменьшением энтропии передает теплоту рабочему телу на процессе с увеличением энтропии, т.е. греет само себя за счет внутренней теплоты. Эти циклы называются регенеративными (регенерация – восстановление, возобновление, возмещение и т.п.) или обобщенными циклами Карно. Последнее название объясняется тем, что таких циклов может быть сколь угодно много, а цикл Карно является их частным случаем.

Для доказательства вышеприведенного утверждения рассмотрим регенеративный обратимый цикл 1234 с изотермическими источниками теплоты (рис.8.10) и сравним его термический КПД с КПД цикла Карно 12АВ, имеющего такие же температуры источников теплоты Т₁ и Т₂.

П 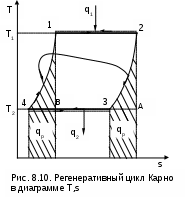одвод внешней теплоты q₁ к рабочему телу в регенеративном цикле осуществляется на процессе 12, а отвод внешней теплоты q₂ осуществляется на процессе 34. Теплота q_р с процесса 23 обратимо передается на процесс 41. Это внутренняя теплота, она называется теплотой регенерации, поскольку рабочее тело греет само себя. Теплота процесса 23 равна по модулю теплоте процесса 41, следовательно, в Т,s- диаграмме площади под этими процессами одинаковы, а сами процессы представляют собой эквидистантные кривые. Эти кривые могут иметь любую конфигурацию.

Поскольку в Т,s- диаграмме процесс 23 эквидистантен по горизонтали процессу 41, то отрезок 12 равен отрезку 34 и отрезку ВА. Следовательно, у обоих циклов одинаковые q₁ и q₂, а соответственно равны _t и η_t=1-Т₂/Т₁, т.е. цикл 1234 эквивалентен циклу Карно 12АВ.

Более простое доказательство равенства отрезков 12 и 34 а соответственно и равенство КПД этих циклов следует из равенства по модулю изменений энтропий горячего и холодного источников теплоты для всех обратимых циклов: s₁-s₂=-(s₃-s₄). Это будет показано при рассмотрении обратимого преобразования теплоты в работу.

Дадим определение регенеративного (обобщенного) цикла Карно.

Регенеративным (обобщенным) циклом Карно называется любой обратимый цикл, осуществляемый между двумя источниками теплоты с постоянными температурами.

Регенерация нашла широкое применение в паротурбинных и газотурбинных установках. Естественно, в реальных циклах невозможно осуществить обратимую передачу теплоты q_p c одного процесса рабочего тела на другой (в обратимом теплообменнике поверхность нагрева должна иметь бесконечно большую величину), но принцип регенеративного теплообмена позволяет частично приблизить КПД данного реального цикла к КПД цикла Карно, имеющего такие же источники теплоты.

8.1.5. Теорема Карно

Сади Карно доказал очень важное свойство предложенного им цикла, которое получило название теоремы Карно и было сформулировано им в следующем виде:

термический КПД обратимого цикла, осуществляемого между источниками теплоты с постоянными температурами, не зависит от свойств рабочего тела, при помощи которого этот цикл осуществляется.

Данное утверждение очевидно для цикла Карно с рабочим телом в виде идеального газа, поскольку его КПД зависит только от температур горячего и холодного источников теплоты (η_t=1-Т₂/Т₁). Однако КПД такого цикла Карно вывел на основании уравнений идеального газа для изотермических и адиабатных процессов. Определение энтропии реального газа как функции состояния нами пока дано голословно, без доказательств. Поэтому изображать цикл Карно в Т,s- диаграмме для реального газа и делать какие - либо заключения о его КПД применительно к реальным рабочим телам пока преждевременно.

Д
оказательство теоремы Карно ведется методом от противного. Принимаются два источника теплоты с постоянными температурами: горячий – с Т₁ и холодный – с Т₂. Используя эти источники теплоты, предположим, что две машины осуществляют обратимый цикл Карно (рис.8.11), который для первой машины соответствует циклу двигателя – прямой цикл, а для второй машины – циклу теплового насоса – обратный цикл. Причем в качестве рабочего тела в первой машине используется идеальный газ, а во второй – реальное вещество, например водяной пар. Обозначим КПД газового цикла как η_t, а КПД парового цикла – η_t^*.

Примем одинаковыми по модулю величины теплоты горячего источника Q₁ для обоих циклов, то есть сколько теплоты подводится в газовый цикл двигателя, столько же теплоты производится в паровом цикле теплового насоса. Таким образом, получается, что горячий источник теплоты в нашей системе, состоящей из двух машин, исключается.

Предположим, что теорема Карно не верна и КПД газового цикла больше, чем КПД парового цикла (η_t>η_t^*). В соответствии с этим предположением работа, произведенная газовым циклом, L будет больше работы L^*, затраченной на осуществление парового цикла:

L = Q₁η_t , L^* = Q₁η_t^*, ΔL = L - L^* = Q₁(η_t - η_t^*) > 0.

Таким образом оказалось, что в системе при использовании только одного холодного источника теплоты была получена работа. Это противоречит второму закону термодинамики, следовательно, η_t не может быть больше η_t^*.

Таким же способом можно доказать, что η_t^* не может быть больше η_t. Для этого достаточно поменять местами рабочие тела в машинах.

В результате проведенного анализа делаем вывод, что КПД обратимых циклов Карно рассматриваемых машин могут быть только одинаковыми, т.е. эти КПД не зависят от свойств рабочего тела. Это и требовалось доказать.
8.1.6. Термодинамическая шкала температур.

Теорема Нернста – третье начало термодинамики

Температура относится к интенсивным термодинамическим параметрам состояния тел. Определение ее осуществляется через экстенсивные свойства тел, например через изменение объема жидкости в бытовом термометре. Для таких термометров могут быть приняты различные равномерные температурные шкалы, в которых могут быть приняты одинаковыми значения температур только в двух опорных точках. При всех других значениях температур различные термометры будут давать различные показания.

Например, возьмем два жидкостных термометра с различными свойствами жидкостей в них (рис.8.12). В цилиндрических столбиках этих термометров можно добиться одинакового уровня при температуре t₀ путем их наполнения при данной температуре, при этом можно подобрать диаметры цилиндров таким образом, чтобы при температуре t₁ их уровни тоже были одинаковыми. Однако в этих цилиндрах при температурах, отличных от t₀ и t₁, уровни жидкостей совпадать не будут, из-за различных изменений объемов жидкостей с различными термодинамическими свойствами.

З 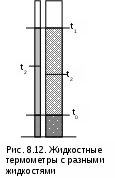ависимость единиц измерения температуры от свойств вещества, используемого в термометре, объясняет наличие многообразия температурных шкал: Цельсия, Реомюра, Фаренгейта и т.д. Все это затрудняет использование их показаний для выполнения расчетов и сопоставления термодинамических параметров различных веществ.

Теорема Карно позволила обосновать абсолютную термодинамическую шкалу температур, которая не зависит от свойств веществ.

П ринцип построения такой шкалы основан на создании последовательной цепочки циклов Карно, каждый из которых использует теплоту q₂ предыдущего цикла как теплоту q₁ для последующего цикла (рис.8.13). Например, в цикле 1234 совершается работа _t, а его отведенная теплота q₂ используется в виде подведенной теплоты q₁ в цикле 4356 и т.д. Приняв работу всех циклов одинаковой (_t=const), получим равенство температурных интервалов, в котором реализуется каждый цикл (T=const), поскольку все они осуществляются в одинаковых диапазонах изменения энтропии (s=const):

.

Получается, что это изменение температуры пропорционально работе цикла Карно.

Построенная на таком принципе температурная шкала будет абсолютной, т.е. не зависящей от свойств вещества, поскольку показатели экономичности цикла Карно не зависят от свойств рабочего тела. В таком термометре, используя любое вещество, совершив одинаковую работу, получим одинаковое изменение его температуры.

В международной системе единиц (СИ) в качестве единицы абсолютной – термодинамической шкалы температур – принят кельвин (название в честь Томсона лорда Кельвина, обосновавшего в 1848 г. абсолютную термодинамическую шкалу температур).

Кельвин – единица измерения температуры по термодинамической шкале, для которой тройной точке воды соответствует значение 273,16 К. Это число выбрано исходя из того, чтобы один градус Цельсия равнялся одному градусу Кельвина. Температура таяния льда при нормальном давлении на 0,01º ниже температуры тройной точки воды, следовательно, 0 ºС соответствует 273,15 К.

Однако практически реализовать обратимый цикл Карно невозможно, поэтому для измерения абсолютной температуры используют газовые термометры, в которых газ находится при низком давлении и подчиняется уравнению Клапейрона – Менделеева: Pv=RT. При постоянном объеме газа в этих термометрах абсолютная температура пропорциональна давлению, что позволяет измерить абсолютную температуру газа через его давление: T=Pv/R.

При значении температуры холодного источника 0 К для обратимого цикла Карно КПД равен единице. В этом случае вся подведенная теплота горячего источника должна превратиться в работу. В случае температуры холодного источника меньше 0 К в цикле Карно оказалось бы получено больше работы, чем подведено теплоты, что противоречит первому закону термодинамики. Таким образом, был сделан вывод о невозможном существовании тел с температурой меньше 0 К.

Вопрос о возможности существования тел с температурой равной 0 К относится к началу ХХ века. Занимаясь теоретическими и экспериментальными исследованиями в области очень низких температур, близких к 0 К, В.Нернст обнаружил, что при приближении к температуре 0 К теплоемкости всех веществ стремятся к нулю. Используя исследования Нернста, М.Планк показал, что вблизи абсолютного нуля все процессы должны протекать без изменения энтропии. На основании этого анализа Планк высказал предположение, что при температуре, равной 0 К для всех веществ, находящихся в равновесном состоянии, энтропия обращается в нуль. Эти утверждения Нернста и Планка составляют содержание третьего начала термодинамики.

Пользуясь третьим началом термодинамики, можно доказать, что абсолютный нуль температуры недостижим. На этом основании третий закон термодинамики может быть сформулирован в следующем виде:никаким способом невозможно охладить тело до температуры абсолютного нуля, т.е. абсолютный нуль температуры недостижим. Формулировку третьего начала термодинамики, близкую к этой, дал Нернст, поэтому она и получила название теоремы Нернста.

Утверждение о недостижимости абсолютного нуля температуры не связано со вторым законом термодинамики. Из этого утверждения лишь следует, что КПД цикла Карно всегда меньше единицы.
8.2. Энтропия реальных тел и ее изменение в необратимых

процессах. Объединенное уравнение первого и второго

законов термодинамики

Р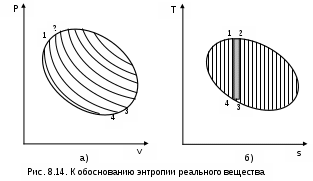
анее (см. разд. 3.1.4) было доказано, что энтропия идеального газа есть параметр состояния. Используя теорему Карно и учение об обратимых циклах, т.е. на базе второго закона термодинамики, можно доказать, что энтропия любого реального тела есть параметр состояния.

Для доказательства этого утверждения рассмотрим в Р,v- диаграмме произвольный внутренне обратимый (без трения) цикл (рис.8.14, а), который совершает реальное рабочее тело. При этом цикл может быть внешне необратимым, в данном случае наличие разности температур между рабочим телом и источником теплоты роли не играет. Разобьем наш цикл, расположенными бесконечно близко друг к другу, адиабатами 14, 23, и т.д. на бесконечно большое количество элементарных циклов. Каждый из этих циклов можно считать циклом Карно, поскольку отрезки, полученные при делении цикла адиабатами, при бесконечно большом количестве последних можно считать изотермами, т.е. отрезок 12 и отрезок 34 заменить изотермами и т.д.

Совокупность этих элементарных циклов Карно эквивалентна нашему циклу, поскольку подведенная и отведенная теплота, а соответственно и работы циклов будут одинаковы. Таким образом, наш цикл можно рассматривать как сумму бесконечного числа таких элементарных циклов Карно.

Для каждого элементарного цикла Карно, не зависимо от свойств рабочего тела, можно записать выражение термического КПД в виде

,

где q₁ и q₂ – количество подведенной и отведенной теплоты;

Т₁ и Т₂ – температуры подвода и отвода теплоты цикла.

Из этого выражения получаются равенства

или ,

при этом последнее выражение записано с учетом того, что отведенная теплота q₂ не взята по модулю (как это сделано в выражении термического КПД), т.е. второе слагаемое этого выражения отрицательное.

Для совокупности всех элементарных циклов Карно, т.е. для всего замкнутого процесса, который совершает реальное рабочее тело, можно записать выражение

, (8.12)

что соответствует интегралу по замкнутому контуру для нашего цикла в виде

. (8.13)

Выражение (8.13) впервые было получено Клаузиусом и получило название интеграла Клаузиуса. Равенство нулю интеграла по замкнутому контуру свидетельствует о том, что под интегралом находится выражение полного дифференциала. Выражение q/T есть полный дифференциал энтропии, т.е. q/T = ds, что позволяет записать выражение (8.13) в виде

. (8.14)

Выражение (8.14) свидетельствует о том, что энтропия определяет состояние реального тела, т.е. она является параметром состояния любого реального тела. Следовательно, после этого доказательства принадлежности энтропии реальных тел к параметру состояния мы можем изобразить наш цикл в T,s- диаграмме (рис.8.14, б).

Понятия энтропии, связанной с механической, электрической или с любой энергией упорядоченного движения, в технической термодинамике не существует. Оно появляется только тогда, когда происходит превращение этих видов энергии в теплоту. То есть есть теплота, есть и изменение энтропии. Являясь параметром состояния, энтропия, а точнее ее изменение, характеризует термодинамические процессы с точки зрения второго закона термодинамики.

Для обратимого процесса, используя первый закон термодинамики, изменение энтропии можно записать в виде выражения

. (8.15)

Для необратимого термодинамического процесса часть работы расширения за счет трения преобразуется в теплоту трения и усваивается телом. Поскольку в данном процессе будет присутствовать внешний и внутренний (за счет трения) подвод теплоты к телу, то и изменение энтропии (а следовательно, и изменение термодинамического состояния тела) будет определяться как внешней теплотой, так и теплотой трения. Для необратимого термодинамического процесса изменение энтропии тела можно представить в виде выражения

, (8.16)

где q = du + Pdv - l_тр = du + Pdv - q_тр – количество теплоты, полученное телом извне (внешняя теплота);

q_тр = l_тр – количество теплоты, полученное телом за счет потерь работы расширения на трение (теплота трения);

q* = q + q_тр = du + Pdv – полное количество теплоты, полученное телом (это выражение первого закона термодинамики для необратимого процесса).

Поскольку в реальном необратимом процессе теплота трения всегда величина положительная (q_тр>0), то для необратимого процесса справедливо соотношение

. (8.17)

Для обратимого процесса теплота трения отсутствует, что приводит к соотношению вида

. (8.18)

Выражения (8.17) и (8.18) можно рассматривать как аналитические выражения второго закона термодинамики для термодинамического тела.

И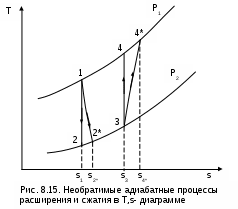
спользуя эти выражения, можно дать следующую формулировку второго закона термодинамики для тела – необратимость термодинамического процесса для тела приводит к увеличению изменения энтропии необратимого процесса по сравнению с изменением энтропии аналогичного обратимого процесса, при том же количестве подведенной внешней теплоты.

Такое увеличение энтропии тела для необратимого процесса, по сравнению с аналогичным обратимым, наглядно демонстрируется на примере адиабатных процессов (рис. 8.15). Адиабатные процессы широко используются в технике – процессы расширения газа или пара в турбине, сжатия воды в насосе или газа в компрессоре. Для обратимых процессов q=0 и ds=0, т.е. обратимая адиабата является изоэнтропой (процессы 12 и 34). В реальных адиабатных процессах всегда происходит увеличение энтропии, обусловленное наличием трения. Так, для необратимых адиабатных процессов 12* и 34* возрастание энтропии на величину s₂*-s₂ и s₄*-s₃ соответственно, обусловлено только теплотой трения этих процессов.

В связи с тем, что выражение q* = Tds* отражает второй закон термодинамики, объединив его с первым законом термодинамики, можно получить объединенное уравнение первого и второго законов термодинамики в виде выражений

Tds = du + Рdv; (8.19)

Tds = dh - vdР, (8.20)

где ds – изменение энтропии для любого процесса, как обратимого, так и для необратимого (звездочку при энтропии здесь не указывают).

Выражения (8.19) и (8.20) справедливы для любых процессов: обратимых и необратимых. Эти выражения используются для анализа термодинамических процессов и являются исходными для дифференциальных уравнений термодинамики в частных производных.

8.3. Изменение энтропии изолированной системы

Напомним, что изолированная система – это система без энергообмена с окружающей средой. Таким образом, речь пойдет об изменении энтропии системы, состоящей из нескольких тел, в результате энергообмена между ними.

Энтропия системы представляет собой сумму энтропий тел, составляющих эту систему, так как она подчиняется закону сложения (аддитивности) аналогично внутренней энергии и энтальпии.

, (8.21)

где S_с и S_i – полная энтропия системы и i-го тела, входящего в эту систему, Дж;

s_i – удельная энтропия i-го тела, Дж/кг;

m_i – масса i-го тела, кг.

В свою очередь изменение энтропии системы равняется алгебраической сумме изменений энтропий всех тел, составляющих систему:

. (8.22)

Рассмотрим, как изменяется энтропия изолированной термодинамической системы при протекании в ней различных обратимых и необратимых процессов.

8.3.1. Изменение энтропии изолированной системы

при теплообмене

Рассмотрим процесс обратимого теплообмена между двумя телами, имеющими одинаковую постоянную температуру Т₁ (рис. 8.16). В обратимом теплообмене отсутствует разница температур между телами. Первое тело (1т) отдает теплоту Q (процесс 12), и его энтропия уменьшается на величину ΔS₁ = Q/T₁. Второе тело (2т) согласно первому закону термодинамики получает то же количество теплоты (процесс 21), но с обратным знаком (-Q), и его энтропия увеличивается на величину ΔS₂ = - ΔS₁ = -Q/T₁, так как обратимый процесс получения теплоты идет по траектории 21, совпадающей с процессом отвода теплоты 12. Суммарное изменение энтропии этой системы

Δ
S_C = ΔS₁ + ΔS₂ = 0. (8.23)

Выражение (8.23) справедливо для любого случая обратимого теплообмена. Так, при переменной температуре двух тел в случае обратимого теплообмена между ними (рис.8.17) получаем изменение энтропии в этой системы тоже равное нулю:

ΔS_C = ΔS₁ + ΔS₂ = 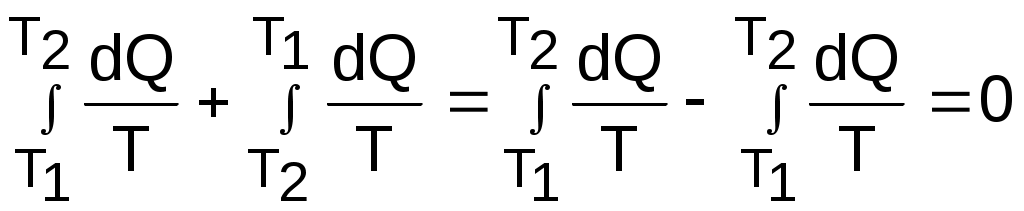. (8.24)

Таким образом, при обратимом теплообмене энтропия системы не изменяется.

Реальный процесс теплообмена между телами происходит при конечной разности температур и поэтому необратим.

Рассмотрим теплообмен между двумя телами, имеющими постоянные температуры Т₁ и Т₂ (рис.8.18). Первое тело отдает теплоту Q (процесс 12), а второе (процесс 34) получает теплоту - Q.

Изменение энтропии системы в этом случае будет больше нуля, так как Т₁>T₂, а Q>0:

ΔS_C = ΔS₁ + ΔS₂ = . (8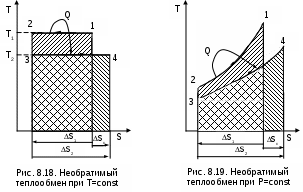.25)

А
налогичная ситуация будет и при необратимом теплообмене между телами с переменной температурой (рис. 8.19), такой процесс возможен в поверхностном теплообменнике.

Таким образом, при необратимом теплообмене энтропия системы возрастает.
8.3.2. Изменение энтропии изолированной системы

при преобразовании работы в теплоту и теплоты в работу

Преобразование механической работы в теплоту наглядно иллюстрируется необратимым процессом трения. Так, если при механическом взаимодействии двух тел с одинаковой температурой Т₁ есть трение, то эта работа трения преобразуется в теплоту трения – L_тр=Q_тр>0. Эта теплота будет воспринята каждым из тел (Q_тр=Q_тр1+Q_тр2), следовательно, возрастет энтропия каждого тела, а соответственно и всей системы.

Увеличение энтропии системы в этом случае можно аналитически показать на примере процесса, в котором температура обоих тел из-за трения увеличивается. Приняв теплоемкости обоих тел постоянными, увеличение энтропии этой системы можно рассчитать как

ΔS_с = ΔS₁ + ΔS₂ = , (8.26)

где m₁, m₂ – массы первого и второго тела;

с₁, с₂ – удельные теплоемкости первого и второго тела;

Т₂, Т₃ – температуры, до которых были нагреты первое и второе тело в результате трения.

Так как T₂>T₁ и T₃>T₁, а с₁>0 и с₂>0, то и ΔS_c>0. Иллюстрацией такого примера может служить добывание огня первобытным человеком путем вращения палочки, зажатой в отверстии деревянного предмета. Необходимо отметить, что преобразование работы трения в теплоту не обязательно должно сопровождаться увеличением температуры тел. Так, в случае трения друг о друга двух кусков льда, имеющих температуру 0 ºС, изменения температуры этих кусков льда не будет, а преобразование работы трения в теплоту будет проявляться в виде плавления льда.

Таким образом, необратимое преобразование механической работы в теплоту всегда приводит к увеличению энтропии системы.

Теперь проанализируем обратный предыдущему процесс преобразования теплоты в работу. В отличие от возможности полного преобразования работы в теплоту полностью преобразовать теплоту в работу невозможно, это было доказано в разд. 8.1.1 и 8.1.2.

И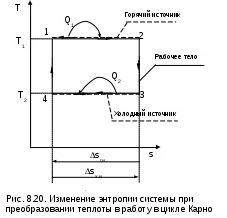
зменение энтропии изолированной системы при обратимом преобразовании теплоты в работу рассмотрим на примере цикла Карно (рис. 8.20). Такая система состоит из горячего (г.и.) и холодного (х.и.) источников теплоты и рабочего тела (р.т.). Изменение энтропии в такой системе соответствует выражению

ΔS_c=ΔS_г.и+ΔS_р.т+ΔS_х.и . (8.27)

Поскольку рабочее тело совершает замкнутый процесс (цикл), то изменение его энтропии равно нулю (ΔS_р.т=0). Процессы подвода теплоты к рабочему телу 12 и отвода теплоты от рабочего тела 34 обратимые, поэтому изменение энтропии горячего источника (отрезок 21) равно изменению энтропии холодного источника теплоты (отрезок 43), взятому с обратным знаком (ΔS_г.и = - ΔS_х.и). В результате получили, что изменение энтропии в этой системе

ΔS_c=ΔS_г.и+ΔS_р.т=0 . (8.28)
Этот вывод о неизменности энтропии системы (ΔSc=0) при обратимом преобразовании теплоты в работу справедлив для любого обратимого цикла, поскольку любой обратимый цикл можно представить в виде суммы элементарных обратимых циклов Карно.
П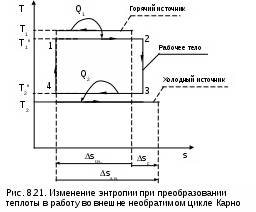
ри необратимом преобразовании теплоты в работу, когда есть разница температур между горячим источником теплоты и рабочим телом на процессе подвода теплоты и между рабочим телом и холодным источником теплоты на процессе отвода теплоты, энтропия системы возрастает (ΔS_c>0). Это наглядно иллюстрируется необратимым циклом Карно (рис. 8.21). В этом случае увеличение энтропии системы обусловлено большим по модулю значением изменения энтропии холодного источника по сравнению с изменением энтропии горячего источника теплоты.

В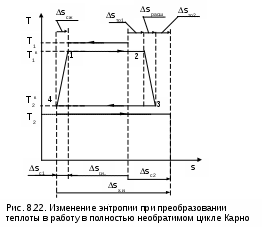
случае, когда кроме внешней необратимости (разности температур между телом, отдающим теплоту, и телом, получающим теплоту) присутствует внутренняя необратимость, вызванная наличием трения в реальных процессах, увеличение энтропии системы будет еще больше по сравнению с циклом, имеющим только внешнюю необратимость. Так, если для цикла Карно с внешней необратимостью (рис.8.21) добавить внутреннюю необратимость, вызванную трением на адиабатных процессах расширения и сжатия рабочего тела, получим полностью необратимый цикл Карно (рис.8.22). У такого цикла увеличение энтропии холодного тела будет еще больше, чем у цикла, изображенного на рис. 8.21, при одинаковых значениях Q₁, Т₁, Т₂, Т₁^к, Т₂^к. Расширение процесса отвода теплоты 34 по отношению к процессу подвода теплоты к рабочему телу 12, обусловленное наличием трения в адиабатных процессов 23 и 41, приводит к увеличению энтропии холодного источника теплоты в полностью необратимом цикле Карно по сравнению с внешне необратимым циклом Карно:

ΔS_c=ΔS_г.и+ΔS_х.и=ΔS_c1+ΔS_с2=ΔS_то1+ΔS_расш+ΔS_то2+ΔS_сж , (8.29)

где ΔS_то1 – увеличение энтропии системы за счет необратимости теплообмена между горячим источником теплоты и рабочим телом;

ΔS_расш – увеличение энтропии за счет необратимости процесса адиабатного расширения рабочего тела;

ΔS_то2 – увеличение энтропии системы за счет необратимости теплообмена между рабочим телом и холодным источником теплоты;

ΔS_сж – увеличение энтропии за счет необратимости процесса адиабатного сжатия рабочего тела.

Принцип возрастания энтропии в изолированной системе относится к любому необратимому циклу теплового двигателя, поскольку, используя понятие среднетермодинамической температуры, любой внутренне обратимый цикл рабочего тела можно представить в виде эквивалентного цикла Карно, а процессы горячего и холодного источников теплоты привести к эквивалентным изотермическим процессам.

8.3.3. Принцип возрастания энтропии изолированной системы

В дальнейшем будут рассмотрены и другие необратимые процессы (дросселирование, смешение и т.д.), которые могут протекать в изолированной системе. Все эти процессы сопровождаются возрастанием энтропии системы.

Проведенный анализ приводит к выводу, что для изолированной системы энтропия или остается постоянной, или возрастает:

ΔS_c ≥ 0. (8.30)

При этом если в системе происходят обратимые процессы то ΔSc=0, если необратимые – ΔSc>0. Этот вывод является одной из формулировок второго закона термодинамики: энтропия замкнутой изолированной системы не может уменьшаться.

Поскольку все реальные процессы необратимы, то в случае их прохождения в изолированной системе ее энтропия всегда будет увеличиваться.

Принцип возрастания энтропии имеет большое практическое значение.

1. Указывает на направление протекания процессов. Самопроизвольные процессы, приводящие систему к равновесному состоянию, идут в направлении возрастания энтропии системы. Следовательно, если система находится в неравновесном состоянии, то ее энтропия возрастает –ΔS_с >0.

2. Дает возможность судить о глубине самопроизвольных процессов. Такие процессы идут до достижения максимума энтропии системы – S_c=S_{c мах.} Следовательно, если система находится в равновесном состоянии, то ее энтропия не изменяется (ΔS_c=0).

3. Увеличение энтропии системы служит мерой необратимости протекающих в ней процессов, т.е. второй закон термодинамики дает не только качественную, но и количественную оценку процессов.

Третье значение принципа возрастания энтропии системы более полно будет раскрыто в следующей главе.

8.4. Получение работы в изолированной системе.

Эксергия в объеме и ее потери

Второй закон термодинамики позволяет охарактеризовать условия, при которых возможно получить работу в данной системе. Возможность получения работы в изолированной системе определяется ее неравновесностью. Таким образом, получение работы в системе определяется не запасом энергии в ней (в изолированной системе запас энергии не меняется), а наличием разности давлений, температур, электрических потенциалов и т.д.

В технической термодинамике рассматривается возможность получения механической работы за счет использования внутренней тепловой энергии тел. Поэтому исключим из рассмотрения химические и внутриатомные процессы, действие гравитационных, магнитных, электрических и других полей, а также изменение кинетической энергии видимого движения вещества.

В изолированной термодинамической системе возможно получение механической работы при наличии в ней механической (разность давлений) или термической (разность температур) неравновесности или того и другого одновременно. Например, имеем баллон со сжатым воздухом и тело, имеющее высокую температуру, оба объекта находятся в окружающей среде с постоянными параметрами. В баллоне имеется механическая неравновесность, что позволяет системе получить работу, для этого открывается вентиль баллона и устанавливается воздушная турбина (вертушка). У горячего тела имеется термическая неравновесность, это в свою очередь дает возможность получить работу с помощью теплового двигателя, в качестве холодного тела здесь выступает окружающая среда.

В обоих случаях возможность получения работы исчерпывается, когда система приходит в состояние термодинамического равновесия. Но система может прийти в состояние равновесия и без совершения полезной работы, в результате протекания в ней необратимых процессов. Например, можно выпустить воздух из баллона в атмосферу или охладить горячее тело за счет его взаимодействия с окружающей средой без совершения полезной работы.

Таким образом, при переходе системы из неравновесного состояния в равновесное величина полезной работы зависит от характера процесса такого перехода. Наибольшая работа получается в том случае, когда система переходит в равновесное состояние при протекании в ней только обратимых процессов. При протекании таких процессов отсутствуют потери возможной работы на трение и на необратимый теплообмен, а обратимые циклы имеют максимальный КПД, т.е. максимальная доля теплоты горячего источника превращается в работу.

Проанализировав вышеизложенное, можно сделать два важных вывода, которые имеют непосредственное отношение ко второму закону термодинамики.

1. В изолированной системе возможно получить работу только в том случае, если она не находится в состоянии термодинамического равновесия. Работоспособность системы исчерпывается при достижении в ней равновесного состояния.

2. Наибольшая возможная работа может быть получена при переходе системы из неравновесного состояния в равновесное, при протекании в ней только обратимых процессов.

8.4.1. Эксергия в объеме

В технической термодинамике наибольший интерес представляет возможность получения работы в системе, состоящей из тел и внешней среды, находящихся в неравновесном состоянии. Окружающая среда в большинстве энергетических установок выступает в качестве холодного источника теплоты: водоемы для ТЭС и АЭС, окружающий воздух для ДВС и ГТУ и т.п. Тела, не находящиеся в равновесном состоянии с окружающей средой: продукты сгорания органического топлива, тепловыделяющие элементы ядерных реакторов и т.п. –, представляют собой горячие источники теплоты, т.е. они выступают в роли потенциальных источников работы. Для оценки максимально возможного количества полезной работы, которое может быть получено в таких системах, в 1955 г. югославским ученым З. Рантом было введено понятие эксергии [5, 6].

Эксергией в объеме называется максимально возможная полезная работа постоянной массы вещества в закрытой системе. Она может быть получена при переходе данного вещества (тела) из неравновесного состояния в состояние равновесия с окружающей средой только по обратимым процессам.

Для иллюстрации понятия эксергии в объеме рассмотрим газообразное тело в цилиндре под поршнем (рис. 8.23). Тело имеет параметры P₁, T₁, окружающая среда имеет параметры P_ос, T_ос. Пусть эта система находится в неравновесном состоянии, т.е. P₁ ≠ P_ос и T₁ ≠ T_ос. В соответствии с определением эксергии в такой системе получается максимальная полезная работа при обратимом переходе тела из начального состояния в состояние полного термодинамического равновесия с окружающей средой.

Таким образом, эксергии будет соответствовать работа на штоке поршня при обратимом переходе тела из первоначального состояния (I с.) с параметрами Р₁, Т₁, U₁, S₁ в состояние его термодинамического равновесия с окружающей средой (II с.), когда его давление и температура будут такими же, как и у окружающей среды, Р_ос, Т_ос, а внутренняя энергия и энтропия тела будут определяться как функция этих параметров – U_ос=F(Р_ос,Т_ос), S_ос=f(Р_ос,Т_ос).

А налитическое выражение для определения эксергии получается из выражения первого закона термодинамики для тела, находящегося в закрытой системе, при совершении телом обратимых процессов.

Первый закон термодинамики для обратимого процесса имеет вид

Q = U_ос - U₁ + L. (8.31)

Количество теплоты, подведенное к телу в нашем примере, можно рассчитать через параметры его состояния на основании следующих положений.

Поскольку система состоит только из нашего тела и окружающей среды, то количество теплоты, подведенное к телу, равно взятому с обратным знаком количеству теплоты, отданному окружающей средой – Q = -Q_ос (в соответствии с первым законом термодинамики).

В системе происходят только обратимые процессы, следовательно, в соответствии со вторым законом термодинамики изменение энтропии такой системы равно нулю – ΔS_с=ΔS_т+ΔS_ос=0, а изменение энтропии тела равно изменению энтропии окружающей среды, взятому с обратным знаком – ΔS_т=-ΔS_ос.

Температура окружающей среды не изменяется, следовательно, теплоту окружающей среды можно представить в виде выражения, соответствующего изотермическому процессу:

Q_ос = T_ос ΔS_ос. (8.32)

Теплоту, полученную телом, можно рассчитать по выражению (8.32), взяв его с обратным знаком и выразив изменение энтропии окружающей среды через изменение энтропии самого тела:

Q = - Q_ос = - T_осΔS_ос = T_осΔS_т = T_ос(S_ос - S₁), (8.33)

где - S₁, S_ос – энтропия тела в начальном состоянии и в состоянии равновесия с окружающей средой (при Р_ос и Т_ос).