пособие. ТТД ч1 учебное пособие. Техническая термодинамика

• Название: Техническая термодинамика
• Анкор: пособие
• Дата: 02.02.2023
• Размер: 4.15 Mb.
• Имя файла: ТТД ч1 учебное пособие.doc
• Тип: Учебное пособие; #917693
• страница: 18 из 19

При изменении объема тело совершает работу L, но всю эту работу как полезную рассматривать нельзя. Часть работы расширения тела L расходуется на перемещение внешней среды, т.е. в нашем примере при движении поршня он перемещает внешнюю среду. Эта работа называется внешней, а так как давление внешней среды не изменяется, то она может быть подсчитана в виде выражения

L_вн = P_ос (V_ос - V₁), (8.34)

где V₁ и V_ос – объем тела при начальных параметрах и при давлении и температуре окружающей среды.

Таким образом, максимальная полезная работа будет представлена в виде разности работы расширения тела и внешней работы:

L_max.п = Е = L - L_вн = Q - (U_ос - U₁) - L_вн =

= T_ос(S_ос - S₁) - (U_ос - U₁) - P_ос (V_ос - V₁). (8.35)

После деления правой и левой частей выражения (8.35) на массу тела получается расчетное выражение удельной максимально полезной работы, которое и является аналитическим выражением эксергии постоянной массы вещества в закрытой системе:

e = (u₁ - u_ос) - T_ос(s₁ - s_ос) + P_ос(v₁ - v_ос). (8.36)

В выражении (8.36) параметры начального состояния тела в разностях поставлены на первое место для лучшего восприятия формулы. Из выражения (8.36) видно, что эксергия при неизменном состоянии внешней среды является функцией состояния вещества, т.е. ее можно представить в виде

e = u₁ - T_ос s₁ + P_ос v₁ - const, (8.37)

где постоянная определяется состоянием внешней среды.

Эксергию в объеме можно представить графически в виде площади в термодинамических диаграммах Р,v и Т,s.

На рис. 8.24 и 8.25 эксергия идеального газа, имеющего параметры P₁, T₁, v₁, u₁, s₁, представлена в виде площади 1а2b1.

В данном примере обратимый переход идеального газа из первоначального состояния (точка 1) в состояние равновесия с окружающей средой (точка 2) осуществляется по обратимой адиабате 1а при s₁=const и обратимой изотерме а2 при Т_ос=const.

В P,v- диаграмме площади под обратимыми процессами 1а и а2 представляют работу изменения объема данного газа. Площадь под адиабатой 1а равна изменению внутренней энергии идеального газа в интервале температур Т₁ и Т_ос, т.е. пл.1аа'1'1=l_1а=u₁-u_ос. Площадь под изотермой а2 равна теплоте этого процесса, т.е. пл.а22'а'а= l_а2 = =q_а2=T_ос(s_ос-s₁). Полная работа изменения объема газа на процессе 1а2 будет представлена в виде алгебраической суммы этих площадей, т.е. l_1а2=пл.1аа'1'1+пл.а22'а'а=u₁-u_ос-T_ос(s₁-s_ос). При графическом суммировании этих площадей в диаграмме Р,v необходимо учитывать отрицательный знак работы в процессе сжатия газа а2 (штриховка этой площади выполнена на рис.8.24 в противоположном направлении по отношению к процессу расширения газа 1а).

Д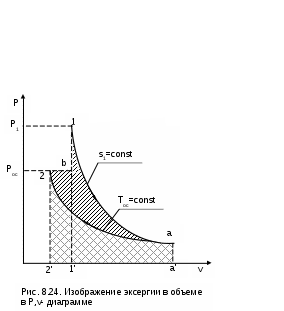
ля получения эксергии необходимо из работы изменения объема газа процесса 1а2 вычесть внешнюю работу e=l_1а2-l_вн. Расчетное выражение внешней работы газа соответствует величине l_вн=P_ос(v_ос-v₁). Внешняя работа, взятая с обратным знаком, в диаграмме Р,v соответствует площади под изобарным процессом 2в, т.е. -l_вн=P_ос(v₁-v_ос)= =пл.2b1'2'2 (работа процесса 2b положительная). В итоге получили, что эксергии газа, имеющего параметры точки 1, в Р,v- диаграмме соответствует работа изменения объема процесса 1а2в и площадь под ним:

пл.1а2b1 = e = (u₁ - u_ос) - T_ос(s₁ - s_ос) + P_ос(v₁ - v_ос).

В
диаграмме Т,s эксергию идеального газа, имеющего параметры точки 1, можно показать в виде площади, перенеся процесс 1а2b из Р,v- диаграммы в диаграмму Т,s (рис.8.25).

Площадь под изохорой v₁=const процесса d1 соответствует изменению внутренней энергии идеального газа в интервале темератур Т₁ и Т_ос, т.е. пл.11'd'd1=u₁-u_ос. Площадь под изотермой Т_ос=const процесса а2 соответствует его теплоте, т.е. пл.а1'2'2а=q_а2=T_ос(s_ос-s₁). Площадь фигуры 2вbb’2’2 соответствует работе изменения объема изобарного процесса 2в, т.е. пл. 2вbb’2’2=l_2d=Р_ос(v₁-v_ос).

В результате алгебраического сложения площадей под процессом d1a2b в диаграмме Т-s получили пощадь фигуры 1a2b1, которая соответствует величине эксергии, т.е.

пл.1a2b1 = e =(u₁ - u_ос) - T_ос (s₁ - s_ос) + P_ос (v₁ - v_ос).
Показать эксергию в объеме для газа в виде площади в диаграммах Р,v и Т,s можно, используя и другие обратимые процессы перехода газа из неравновесного состояния в состояние равновесия с окружающей средой. Обязательным условием такого перехода яляется обратимость всех процессов.

8.4.2. Практическое значение эксергии

Ранее была рассмотрена эксергия газового тела при переходе его в состояние равновесия с окружающей средой по обратимым процессам. В этом случае газ сам выступает в роли рабочего тела.

В теплоэнергетике большое значение имеет использование термической неравновесности источника работы (горячее тело) и внешней среды (холодное тело) посредством рабочего тела, совершающего замкнутый процесс изменения состояния – цикл. В этом случае источник работы может иметь любые физические свойства. В теплоэнергетических установках это, как правило, газообразные продукты сгорания топлива, тепловыделяющие элементы или первичный теплоноситель (жидкий или газообразный) атомного реактора. В таких установках рабочее тело совершает цикл, источник работы служит теплоотдатчиком, а внешняя среда – теплоприемником.

В теплоэнергетике термодинамический анализ термической неравновесности источника работы и внешней среды с использованием понятия эксергии может быть практически использован в следующих направлениях:

1) для определения максимально полезной работы – эксергии, которая может быть получена в системе при использовании определенного количества первичного теплоносителя (источника работы);

2) для определения влияния необратимости на полезную работу;

3) для выбора рациональных циклов теплоэнергетических установок.

Последовательно рассмотрим эти направления применительно к наиболее характерным случаям.

8.4.2.1. Определение эксергии источников работы, имеющих

термическую неравновесность

Первоначально рассмотрим источник работы с постоянной температурой (бесконечной теплоемкостью), имеющей большее значение, чем температура внешней среды. Примером такого источника работы являются тепловыделяющие элементы в кипящем ядерном реакторе, вырабатывающем насыщенный водяной пар при постоянном давлении.

Для определения эксергии этого источника работы (теплоты) необходимо рассмотреть термодинамическую систему, которая должна включать в себя: горячий источник теплоты с постоянной температурой Т₁ (источник работы), внешнюю среду с постоянной температурой Т_ос (холодный источник теплоты) и рабочее тело (рис.8.26).

В рассматриваемой системе, при использовании количества теплоты Q₁, передаваемого от горячего источника теплоты рабочему телу, максимально полезная работа, или эксергия, может быть получена только при неизменной энтропии системы (ΔS_c = 0), т.е. при прохождении в ней только обратимых процессов. Выполнение этого условия возможно только при осуществлении в нашей системе обратимого цикла Карно (рис. 8.26) в интервале температур Т₁ и Т_ос. Только в этом случае в нашей системе не будет протекать никаких необратимых процессов, не будет возрастания энтропии системы и не будет потерь возможной работы.

Следовательно, максимально полезная работа – эксергия, получаемая в этом случае, будет соответствовать работе обратимого цикла Карно 1234: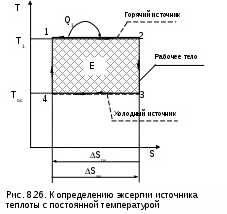


. (8.38)

Множитель (T₁-T_ос)/T₁ в выражении 8.38 представляет термический КПД данного цикла Карно, он называется эксергетической температурой. Всегда целесообразно иметь большее значение эксергетической температуры, поскольку в этом случае эксергия источника работы также будет иметь большее значение.

В случае если источник работы имеет конечную теплоемкость и температуру выше, чем температура окружающей среды, и находится в механическом равновесии с внешней средой (Р=Р_ос), он может перейти в состояние термического равновесия с внешней средой при его охлаждении по изобаре Р=const.

Н а практике существует множество источников работы такого типа: продукты сгорания органического топлива, горячие газы, пары, жидкости и т.п.

Рассмотрим определение эксергии таких источников работы на примере продуктов сгорания топлива, охлаждающихся от температуры Т₁ до температуры окружающей среды Т_ос при постоянном атмосферном давлении Р_ос=const (рис.8.27). Для получения работы в этом случае, как и в первом, необходимо, чтобы кроме источника работы система включала внешнюю среду с постоянной температурой Т_ос и рабочее тело. Получение максимально полезной работы в этой системе также возможно только при протекании в ней обратимых процессов, т.е. при отсутствии увеличения энтропии системы (ΔS_c = 0). В соответствии с этим условием рабочее тело должно совершать цикл 1231, поскольку только в этом случае изменение энтропии продуктов сгорания (процесс 12) будет равно изменению энтропии внешней среды (процесс 23) с обратным знаком. Максимально полезная работа, или эксергия, источника работы в этом случае будет равна площади 1231. Любой другой цикл рабочего тела не будет полностью обратимым и даст меньшую работу.

8.4.2.2. Определение влияния необратимости на полезную работу в изолированной системе

Как было установлено ранее, любая необратимость связана с возрастанием энтропии изолированной системы. Рассмотрим, как различные виды необратимости влияют на возможность получения полезной работы в изолированной системе.

Необратимый теплообмен

Необратимый теплообмен обусловлен наличием разности температур между телами.

Рассмотрим в T,S- диаграмме сначала случай необратимого теплообмена между двумя телами с постоянными температурами Т₁ и Т₂ (рис. 8.28). Кроме указанных тел система включает в себя окружающую среду с постоянной температурой Т_ос, которая при оценке эксергии используется в качестве охладителя. Как было установлено ранее, энтропия такой системы возрастет на величину

, (8.39)

где Q – теплота, полученная телом с температурой Т₂ от тела с температурой Т₁.

Отличие эксергии первого тела от второго (потеря эксергии) в этом случае будет представлено разницей работ обратимых циклов Карно (Е₁=пл.16521 и Е₂=пл.34753)

. (8.40)

Эта потеря эксергии в T,S- диаграмме представляет площадь

-ΔE=T_осΔS_c=пл.674'1'6.

П
оскольку энтропия системы в нашем примере увеличивается (ΔS_c>0), то в результате необратимости теплообмена эксергия тела с меньшей температурой будет меньше, чем эксергия тела с большей температурой. Следовательно, наличие необратимости теплообмена приводит к снижению работоспособности системы, т.е. к потере возможной работы системы (эксергии).

В случае необратимого теплообмена между телами с переменной температурой (рис. 8.29) будет аналогичный результат. Здесь доказательств не требуется, так как любой процесс подвода и отвода теплоты в обратимом цикле в T,S- диаграмме можно представить в виде изотермического процесса со среднетермодинамической температурой. На рис.8.29 эксергии тел и уменьшение эксергии вследствие необратимого теплообмена представляют следующие площади:

Е₁=пл.12561, Е₂ = пл.34753, -ΔЕ = Т_осΔS_c = пл.674'1'6.

Полученное выражение применимо ко всем необратимым процессам. Сформулированное положение, что потеря возможной работы системы (эксергиии) представляет собой произведение абсолютной температуры окружающей среды на увеличение энтропии системы, вызванное необратимостями происхдящих в ней процессов, носит название теоремы Гюи – Стодолы в честь ученых, установивших эту закономерность. Аналитическое выражение этой теоремы имеет вид

-ΔE = T_ос ΔS_c , (8.41)

где -ΔE – потеря максимально возможной работы системы - эксергии;

Т_ос – абсолютная температура окружающей среды;

ΔS_c – возрастание энтропии системы за счет необратимости процессов.

Справедливость теоремы Гюи–Стодолы в дальнейшем будет многократно подтверждена.

Необратимость, обусловленная преобразованием работы

в теплоту путем трения

Р 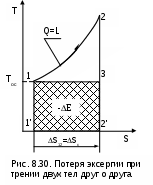ассмотрим пример преобразования работы в теплоту трения и оценим влияние этой необратимости на получение возможной работы в изолированной системе.

Предположим, что две металлических пластины трутся друг о друга. Перемещение этих пластин вызвано затратой механической работы в изолированной системе. В результате трения пластины нагреваются, т.е. механическая работа преобразуется в теплоту трения. Обозначим механическую работу, которая преобразовалась в теплоту трения, величиной L=Q и рассмотрим эту ситуацию в диаграмме T,S (рис. 8.30). Поскольку пластины восприняли (внутреннюю) теплоту трения, то их энтропия увеличилась, следовательно, увеличилась и энтропия данной изолированной системы – ΔS_c=S₂-S₁>0. Если теплоту трения Q этих пластин использовать даже в обратимом цикле, где охладителем является окружающая среда, то полученная максимально возможная работа в этой системе будет соответствовать эксергии источника теплоты в виде этих нагретых пластин – Е=пл.1231. Эта максимально возможная работа будет меньше теплоты трения на величину площади 132'1'1, которая соответствует произведению T_осΔS_c. Следовательно, необратимость процесса преобразования работы в теплоту трения привела к потере возможной работы, которая тоже может быть определена по теореме Гюи–Стодолы (-ΔL=L-E=T_осΔS_c).

Необратимость при расширении газа в вакуум

Рассмотрим жесткий сосуд, имеющий объем V и разделенный перегородкой на две части (рис.8.31, а). Одну часть сосуда с объемом V₁ занимает газ при температуре Т_ос, равной температуре окружающей среды, в другой части сосуда – абсолютный вакуум. Поскольку газ и окружающая среда имеют одинаковые температуры, такая термодинамическая система находится в равновесном состоянии. Если убрать перегородку (рис.8.31, б), произойдет расширение газа в вакуум, в результате чего газ займет весь объем сосуда V. Это типичный необратимый процесс, сопровождающийся увеличением энтропии системы и потерей возможной работы (эксергии).

П
олучим расчетное выражение для изменения энтропии в такой системе при расширении газа в вакуум и убедимся, что энтропия системы возрастет.

Поскольку процесс расширения газа быстротечен, считаем, что теплообмен газа с окружающей средой отсутствует, т.е. Q=0. При расширении газа объем сосуда не изменяется и механической работы он не совершает, т.е. L=0. В соответствии с первым законом термодинамики (Q=U₂-U₁+L) при Q=0 и L=0 изменения внутренней энергии газа в такой системе нет, т.е. U₂=U₁. Применительно к идеальному газу нет и изменения температуры в такой системе, Т₂=Т₁. Таким образом, изменение энтропии системы равно изменению энтропии газа, т.к. теплообмен газа с окружающей средой отсутствует, а изменение энтропии идеального газа может быть рассчитано по изотермическому процессу в виде выражения

. (8.42)

Поскольку при расширении газа его объем увеличивается, то в соответствии с уравнением (8.42) энтропия системы возрастает.

Определить потерю максимально возможной работы (эксергии) при расширении идеального газа в вакуум можно, заменив в нашей системе перегородку поршнем со штоком (рис.8.31, б) осуществив обратимое изотермическое расширение газа. Таким образом, газ будет совершать такой же изотермический процесс, как и в первом случае, но на штоке поршня будет получена полезная механическая работа. В соответствии с первым законом термодинамики применительно к газу эта работа равна теплоте (L=Q), поскольку изменения внутренней энергии идеального газа в изотермическом процессе расширения нет. Рассчитать эту работу можно по формуле изотермического процесса:

. (8.43)

В соответствии с первым законом термодинамики для всей термодинамической системы эта работа должна быть равна теплоте, полученной газом в обратимом процессе изотермического расширения от окружающей среды, т.е. -Q_ос=Q=L. Другими словами, полезная работа в нашей системе была получена за счет подвода теплоты к газу от внешней среды. При осуществлении такого расширения газа в вакуум энтропия окружающей среды уменьшится на такую же величину, на какую увеличится энтропия газа:

, (8.44)

т.е. изменение энтропии в нашей системе

ΔS_c = ΔS_газ + ΔS_оc = 0 ,

следовательно, в ней протекают только обратимые процессы.

В случае полностью необратимого расширения газа в вакуум вся возможная полезная работа (8.43) теряется. Оценить потерю этой работы, как любого необратимого процесса, позволяет теорема Гюи–Стодолы, выражение которой получается из уравнений (8.42) и (8.43):

.

Необратимость при диффузионном смешении газов

с одинаковыми температурами и давлениями

Смешение двух различных газов, имеющих одинаковые температуры и давления, это тоже необратимый процесс. Рассмотрим такой процесс на примере двух различных газов, находящихся в сосуде объемом V, разделенном перегородкой на две части с объемами V₁ и V₂ (см. рис.8.32, а). В этих частях сосуда находятся разные газы при одинаковых давлениях P и температурах, равных температуре окружающей среды T_ос. Для упрощения анализа процесса смешения будем считать, что оба газа идеальные.

Если убрать перегородку, то произойдет типично необратимый процесс диффузионного смешения газов с возрастанием энтропии системы. В соответствии с законом Дальтона каждый газ при расширении ведет себя так, как будто другого газа в сосуде нет. При этом в конце процесса смешения каждый газ будет занимать весь объем сосуда V, а парциальные давления газов будут определяться выражениями

.

К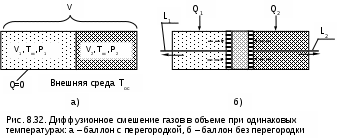
ак и при расширении в вакуум, диффузионное смешение газов в нашем примере будет происходить без теплообмена с окружающей средой (Q=0) и без совершения работы изменения объема (L=0). Следовательно, в соответствии с первым законом термодинамики изменения внутренней энергии в нашей системе нет (U_см-(U₁+U₂)=0). Поскольку внутренняя энергия идеального газа зависит только от температуры, а температура обоих газов до смешения была одинакова, то и после смешения температура газа останется прежней, т.е. наш процесс смешения будет изотермическим.

Изменение энтропии в такой системе будет соответствовать изменению энтропии газов, поскольку теплообмен газов с окружающей средой отсутствует. Рассчитать изменение энтропии системы можно по формулам изотермических процессов расширения для каждого газа:

. (8.45)

Очевидно, что в процессе диффузионного смешения газов энтропия системы возрастает.

Для того чтобы оценить потерю возможной работы в диффузионном процессе смешения газов, проведем теоретически обратимый процесс диффузионного смешения газов. Для этого заменим перегородку в сосуде с газами двумя полупроницаемыми поршнями со штоками (см. рис.8.32, б). Левый поршень проницаем только для первого газа, а правый поршень – только для второго газа. В результате такого процесса смешения между поршнями образуется смесь газов. При этом на левый поршень действует справа давление (парциальное) только второго газа, на правый поршень действует слева давление (парциальное) первого газа. Поршни будут двигаться в противоположных направлениях, передавая через штоки полезную работу L₁ и L₂ в окружающую среду.

В соответствии с первым законом термодинамики для всей термодинамической системы эти работы должны быть равны теплоте, полученной каждым газом в обратимых процессах их теплообмена с окружающей средой при осуществлении процесса смешения, т.е. L₁=Q₁ и L₂=Q₂. Следовательно, внутренняя энергия каждого газа и всей системы в процессе смешения не изменится, а так как температуры газов одинаковы, то обратимый процесс диффузионного смешения газов будет изотермическим. Работу такого изотермического расширения газов можно рассчитать по формуле



. (8.46)

Изменение энтропии газов в этом процессе будет определяться выражением

,

а изменение энтропии окружающей среды – выражением, в котором теплота, подведенная к газам для окружающей, среды имеет противоположный знак:

.

В результате получилось, что изменение энтропии системы при таком диффузионном смешении газов равно нулю.

.

Следовательно, рассматриваемый процесс обратимый.

Для необратимого диффузионного процесса смешения газов, используя выражения (8.45) и (8.46), получаем очередное подтверждение теоремы Гюи–Стодолы, в соответствии с которой потеря возможной полезной работы за счет необратимости определяется выражением

.

Необратимое преобразование теплоты в работу

при источнике работы с постоянной температурой

Обратимое преобразование теплоты в работу при источнике работы с постоянной температурой рассмотрено в разд. 8.4.2.1. В системе, включающей в себя такой источник теплоты и окружающую среду, обратимое преобразование теплоты в работу соответствует осуществлению идеального цикла Карно, для которого окружающая среда выступает в роли холодного источника теплоты.

В реальных условиях преобразование теплоты в работу сопровождается необратимыми процессами, обусловленными необходимостью наличия разности температур при передаче теплоты от одного тела к другому. Кроме этого присутствует трение (в широком его понимании) при осуществлении реальных процессов рабочим телом в цикле теплового двигателя, в результате чего часть работы преобразуется в теплоту трения.

Рассмотрим необратимое преобразование теплоты в работу при источнике работы с постоянной температурой на примере полностью необратимого цикла Карно, в котором окружающая среда выступает в роли холодного источника теплоты. Такая система включает в себя источник работы с постоянной температурой и внешнюю среду с постоянной температурой, рабочее тело совершает необратимый цикл Карно (рис.8.33). Внешняя необратимость цикла обусловлена разностью температур между горячим телом и рабочим телом (ΔT₁=T₁-T₁^к), и рабочим телом и окружающей средой (ΔT₂=T₂^к-T_ос). Внутренняя необратимость цикла обусловлена наличием трения в процессах адиабатного расширения 23 и сжатия 41.

В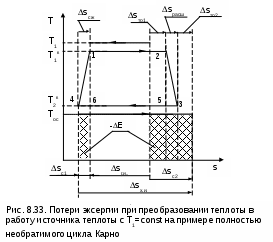
нешняя необратимость за счет ΔT₁ приводит к увеличению энтропии системы на величину S_то1. Внутренняя необратимость увеличивает изменение энтропии системы на величины S_расш и S_сж, что соответствует разности энтропий отрезков 34 и 12. Внешняя необратимость ΔT₂ приводит к увеличению энтропии системы на величину S_то2. Другими словами, увеличение энтропии холодного источника теплоты ΔS_х.и по сравнению с горячим источником теплоты ΔS_г.и обусловлено внешней необратимостью (ΔT₁), внутренней необратимостью адиабатных процессов расширения и сжатия и внешней необратимостью (ΔT₂). В итоге имеем увеличение энтропии нашей системы в виде разности энтропий горячего и холодного источников теплоты, соответствующей величине

ΔS_c = ΔS_г.и+ ΔS_х.и = ΔS_c1+ ΔS_c2.

Потери максимально полезной работы – эксергии – -ΔE нашего источника теплоты будут определяться разностью работ обратимого цикла Карно и полностью необратимого цикла Карно 12341. В соответствии с теоремой Гюи–Стодолы эти потери работы на рис.8.33 равны сумме заштрихованных площадей.

-ΔE = T_ос ΔS_С.

Необходимо отметить, что не вся теплота трения адиабатных процессов расширения и сжатия теряется. Она усваивается рабочим телом, повышая его работоспособность, что проявляется в увеличении работы цикла 12341 по сравнению с работой цикла 12561, в котором отсутствует внутренняя необратимость. Теплота трения адиабатных процессов расширения и сжатия рабочего тела соответствует площадям под процессами 23 и 41 в T,S- диаграмме. Часть этой теплоты трения, соответствующей сумме площадей треугольников 2352 и 1641, преобразуется в работу цикла, а остальная часть передается внешней среде, что и приводит к увеличению энтропии системы за счет внутренней необратимости.

Для оценки полезного использования теплоты трения во внутренне необратимых циклах вводится понятие коэффициента возврата потерь теплоты трения. Это отношение той части теплоты трения, которая используется для получения работы в цикле, к теоретической работе данного внутренне обратимого цикла. Для нашего примера он определяется отношением площадей (см. рис.8.33):

. (8.47)

Необратимое преобразование теплоты в работу

при источнике работы с конечной теплоемкостью

Получение максимально возможной работы (эксергии) от источника теплоты (работы) с конечной теплоемкостью было рассмотрено в разд. 8.4.2.1. Однако осуществить обратимый цикл, позволяющий получить эксергию этого источника работы, практически невозможно.

Рассмотрим пример (рис.8.34) необратимого преобразования теплоты в работу для источника работы, в виде продуктов сгорания органического топлива (процесс АВ), изобарно охлаждающихся от температуры горения топлива до температуры окружающей среды. Для упрощения анализа оценки необратимостей примем, что получение работы в нашем примере будет осуществляться рабочим телом по внутренне обратимому циклу Карно 12341, имеющему температуру отвода теплоты из цикла, равную температуре окружающей среды. Внешнюю необратимость цикла Карно ограничим только разностью температур п
ри передаче теплоты от источника теплоты АD к рабочему телу 12.

Эксергия продуктов сгорания топлива соответствует площади криволинейного треугольника АВСА. Поскольку для передачи теплоты от источника работы к рабочему телу необходима разность температур между ними, то продукты сгорания топлива в процессе DВ будут охлаждаться за счет окружающей среды и в получении работы участвовать не могут. Площадь треугольника ВD4B соответствует потере эксергии за счет необратимого процесса охлаждения уходящих газов в окружающей среде. Оценить потерю этой эксергии можно и через увеличение энтропии системы. Для этого количество теплоты, полученной окружающей средой от уходящих газов, покажем в виде площади под изотермой 4Е, т.е.

Qух=пл.BDD'B'B=пл.E4D'E'E.

В результате такого необратимого охлаждения газов энтропия системы возрастет на величину отрезка Е'В' = ΔS_ух, а потеря эксергии за счет этой необратимости может быть представлена в виде

-ΔE_ух = T_осΔS_ух = пл.ЕВВ'Е'Е = пл.BD4B .

Передача теплоты с процесса АD к рабочему телу на процесс 12 также обусловлена внешней необратимостью. Рабочее тело получает теплоту, соответствующую площади под изобарой AD и равную площади под изотермой 12. В результате этой необратимости изменение энтропии холодного источника теплоты цикла Карно (процесс 43) будет больше, чем изменение энропии горячего источника теплоты (процесс AD) и произойдет увеличение энтропии системы на величину отрезка А'2'=ΔS_то. Необратимость этого теплообмена приведет к потере эксергии, определяемой как

-ΔE_то = T_осΔS_то = пл.С32'А'С .

Общее увеличение энтропии системы в нашем примере будет представлять сумму

ΔS_с = ΔS_ух + ΔS_то,

а общая потеря эксергии источника работы соответствует выражению

-ΔE = (-ΔE_ух) + (-ΔE_то) = T_осΔS_с.

Методы оценки тепловой экономичности реальных циклов

тепловых машин

При осуществлении любого реального необратимого цикла его работа всегда меньше эксергии источника теплоты. Отношение работы, полученной в цикле, к эксергии источника теплоты начального состояния называется эксергетическим КПД.

. (8.48)

Для полностью обратимого цикла эксергетический КПД равен единице. Для необратимого цикла эксергетический КПД показывает, какую долю потенциально возможной работы – эксергии – данного источника теплоты удалось преобразовать в полезную работу цикла.

Для примера, приведенного на рис.8.34, эксергетический КПД представляет отношение площадей:

.

Работу цикла можно представить в виде разности эксергии источника теплоты и ее потерь за счет необратимостей:



Метод оценки экономичности цикла тепловой машины посредством расчета потерь эксергии источника теплоты и определения эксергетического КПД цикла называется эксергетическим методом.

Этот метод позволяет детально оценить потери полезной работы во всех необратимых процессах цикла тепловой машины [5, 6].

Поскольку теорема Гюи–Стодолы -ΔE=T_осΔS_с представляет универсальное выражение для расчета потери эксергии в любом необратимом процессе, а увеличение эксергии системы за счет необратимостей процессов фактически определяет потерю эксергии, то величина ΔS_с выступает в роли оценки экономичности цикла тепловой машины. Метод оценки экономичности цикла тепловой машины, основанный на расчете увеличения энтропии системы за счет необратимостей реальных процессов, протекающих в цикле, называется энтропийным методом. Этот метод позволяет оценить, какую долю в общее увеличение энтропии системы вносит каждый необратимый процесс цикла тепловой машины. Анализ увеличения энтропии системы за счет каждого необратимого процесса и цикла в целом позволяет с помощью энтропийного метода проводить термодинамическую оптимизацию циклов тепловых машин. Для увеличения экономичности цикла необходимо стремиться к снижению увеличения энтропии системы и делать это целесообразно в тех процессах, где увеличение энтропии системы наибольшее.

На практике экономичность циклов тепловых машин оценивают с помощью метода теплового баланса с применением коэффициента использования теплоты, представляющего отношение работы цикла к полной теплоте внешнего источника:

, (8.49)

где L – работа цикл;,

Q_т – теплота внешнего источника (теплота продуктов сгорания топлива и т.п.).

В нашем примере величине Q_т соответствует площадь под процессом АВ, а L=пл.12341. Часть теплоты Q_т не участвует в получении работы и выбрасывается в окружающую среду в виде теплоты уходящих газов Q_ух (площадь под процессом DB). Другая часть теплоты Q_т на процессе AD передается рабочему телу, которое совершает работу L и передает окружающей среде теплоту Q₂, соответствующую площади под процессом 43. Исходя из первого закона термодинамики, для нашей системы можно записать:

L = Q_т - Q_ух - Q₂ . (8.50)

Выражение (8.50) получило название теплового баланса. В этом выражении величины Q_ух и Q₂ представляют потери теплоты Q_т в окружающую среду. Необходимо отметить, что потерь теплоты в окружающую среду в реальном цикле может быть больше: через поверхность парогенератора, регенеративные теплообменники и т.п.

Для нашего примера коэффициент использования теплоты можно представить выражением

. (8.51)

В
качестве использования этого выражения для оптимизации температуры уходящих газов Т_D и соответственно температуры подвода теплоты в цикл Карно Т₁ рассмотрим их влияние на потери теплоты в окружающую среду Q_ух и Q₂ (рис.8.35).

Для упрощения анализа разность температур ΔТ=Т_D-Т₁ будем считать постоянной, т.е. в качестве переменной величины достаточно рассматривать только Т_D=Т_ух. С увеличением Т_ух от минимальной величины, равной Т_ух.min=Т_ос+ΔТ, до максимальной – Т_ух.max=Т_A, потери теплоты с уходящими газами будут увеличиваться от Q_ух=Q_ух.min до Q_ух.max=Q_т, а потери теплоты от рабочего тела Q₂ будут уменьшаться от Q₂=Q_2max до Q_2min=0. Получается, что суммарные потери теплоты в окружающую среду Q_ух+Q₂ имеют минимум. При минимальном значении суммы Q_ух+Q₂, в соответствии с выражением (8.51), будет наибольший коэффициент использования теплоты нашего цикла. Следовательно, оптимальная температура уходящих газов будет соответствовать температуре Т_ух.опт на графике рис.8.35.

Аналогичную оптимизацию температуры уходящих газов можно выполнить на основании эксергетического или энтропийного метода. При этом в качестве критериев оптимального решения применяются величины минимальных потерь эксергии и минимального увеличения энтропии системы.

Все три метода оценки тепловой экономичности циклов тепловых машин имеют практическое применение. Метод теплового баланса наиболее простой, поэтому он широко используется в производственной практике. Эксергетический и энтропийный методы более трудоемкие в расчетной части, но они позволяют детально оценить любую необратимость каждого процесса и ее влияние на тепловую экономичность как всего теплового двигателя, так и отдельного его элемента. При этом можно выполнить расчет только отдельного необратимого процесса для оценки его необратимости, что невозможно в методе теплового баланса, который требует полного расчета всего цикла теплового двигателя. Кроме этого, балансовый метод может дать максимальную величину коэффициента использования теплоты (даже равного единице) при нулевом значении работы цикла (цикл ГТУ, цикл противодавленческой ПТУ), что делает его в этом случае непригодным для оценки экономичности тепловой машины. О таких ситуациях подробно рассказано в [1, 5, 6].

На основании вышеизложенного, эксергетический и энтропийный методы имеют практическое применение в теплоэнергетике в следующих случаях:

1) для оценки необратимостей реальных процессов во всех элементах тепловых машин;

2) при оценке тепловой экономичности тепловых двигателей;

3) при проведения оптимизации параметров рабочих тел и выборе оптимальных схем и циклов тепловых машин.