мой курсач. Техническое задание 2 Описание и обоснование разрабатываемой конструкции 3
 Скачать 274.13 Kb. Скачать 274.13 Kb.
|
5.3. Геометрический расчёт кинематики проектируемой конструкцииПо проведенным кинематическому и прочностному расчетам можно сделать расчет геометрических параметров зубчатых колес (см. рис.2.) , входящих в проектируемы привод. 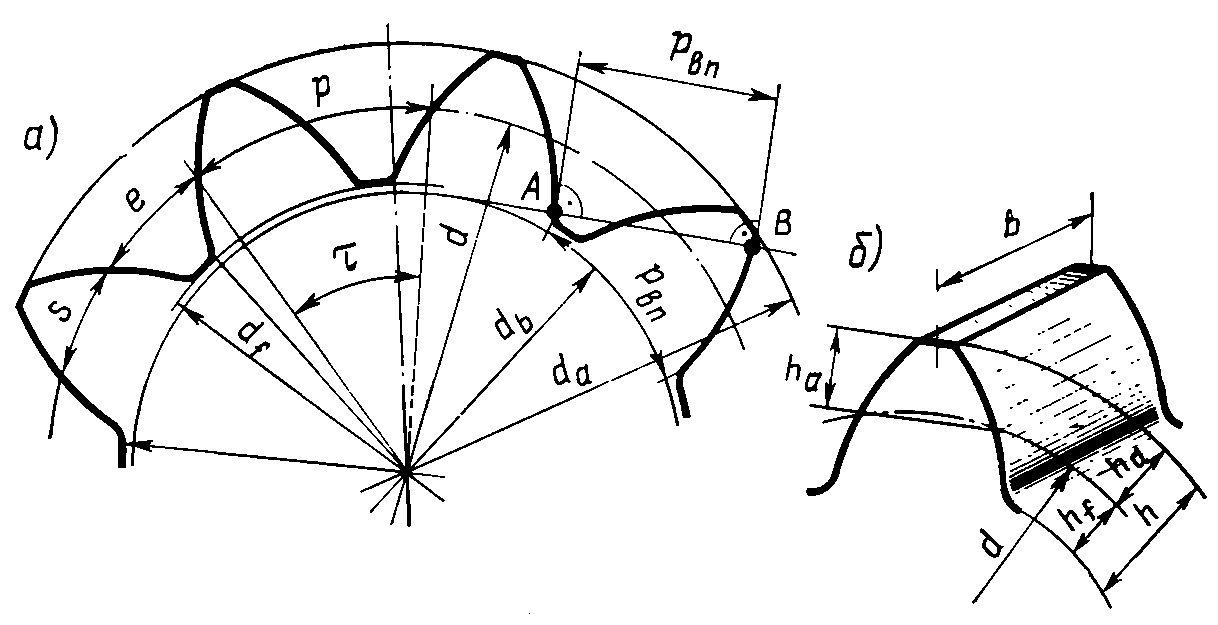 Рис.2. Делительный диаметр d1=m·Z1/cosβ=m·Z1 т.к. колесо прямозубое, то β=0 (22) Диаметр вершин зубьев da=m·z/cosβ+2·m· (ha+x12)=m· (z+2) т.к. ha=1, x12=0 (23) Диаметр впадин df=m·z/cosβ-2·m· (ha+c-x12)=m(z-2-2·c); Так как m≤0.5, то c=0.5. (24) Ширина колес b2 = ψbm·m, (25) где ψbm – коэффициент, равный отношению ширины зубчатого венца к модулю, ψbm =10. Ширина шестерни b1 = b2 + 1,5m (26) Делительное межосевое расстояние aω=0.5·m·(Z1+Z2)/cosβ=0.5·m·(Z1+Z2) (27) Таблица 5.
На этом этапе можно изобразить кинематическую схему редуктора, а также начать предварительную разметку привода. 6. Проектировочный расчет валов и опорЦелесообразно выделить наиболее нагруженный вал в редукторе и выполнить расчёт для него. Самыми нагруженными валами являются последние валы: пятый (выходной) и четвёртый. Расчёт проведём для четвёртого (предпоследнего) вала. 6.1. Проектировочный расчет валаМомент кручения равен 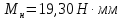 Назначим материал Сталь 45. Диаметр валика определяется из условия  (28) (28)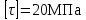 - среднее значение касательных напряжений для стальных валов. - среднее значение касательных напряжений для стальных валов.Расчет диаметра всех валов дает:
Из технологических соображений и по условию ТЗ назначаем диаметры валов из стандартного ряда по ГОСТ 12081-72:
6.1.1. Расчет вала на статическую прочностьДля расчёта выберем предпоследний вал, как наиболее нагруженный. При расчете принимаем:
Из этого следует, что общая длина вала 46 мм Расчет сил, действующих на вал, ведем по формулам:  , (29) , (29)где d – диаметр начальной окружности колеса или шестерни Принимаем d, равным диаметру делительной окружности, т. к. x = 0 Mкр – крутящий момент на валу  , (30) , (30)где α = 20 Значения сил, приложенных к валу:
Изобразим расчетную схему для вала:  Рис.3. Проекции сил, приложенных к валу на плоскость ZX:  Рис.4. Проекции сил, приложенных к валу на плоскость ZY:  Рис.5. Для определения неизвестных реакций X1, X2, Y1, Y2 составим системы уравнений равновесия вала: Плоскость ZX:  Плоскость ZY: 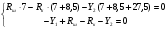 В результате решения уравниний находим:
Эпюры моментов, действующих на вал (все моменты показаны в [Н∙мм]):  Рис.6. 6.1.2. Определение эквивалентных напряженийСогласно энергетической теории:  (31) (31) Определим эквивалентное напряжение в сечении, где действуют окружная и радиальная силы. Здесь действуют изгибающие моменты: в плоскости OZY (25,76 Н*мм) и в плоскости OZX (110 Н*мм), не стоит забывать про крутящий момент (65,55 Н*мм). Найдем нормальное напряжение: 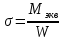 (32) (32)где:  осевой момент сопротивления изгибу в горизонтальной или вертикальной плоскости; осевой момент сопротивления изгибу в горизонтальной или вертикальной плоскости;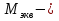 изгибающий момент в сечении. изгибающий момент в сечении.Формула для расчета осевого момента сопротивления изгибу для круглого сечения имеет вид: 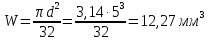 (33) (33)Рассчитаем эквивалентный момент в сечении, где действуют силы:  (34) (34)Определим напряжение изгиба: 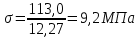 Касательное напряжение рассчитаем по формуле: 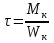 (35) (35)где 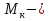 крутящий момент, крутящий момент, момент сопротивления кручению; момент сопротивления кручению; (36) (36)Определим напряжение изгиба: 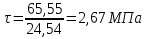 Таким образом, напряжение в опасном сечении: 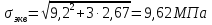 Переходим к сравнению напряжения с допускаемым. Должно выполняться условие 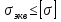 где 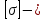 допустимое напряжение. допустимое напряжение.Вал при работе совершает вращательные движения, а значит, находится под действием переменной нагрузки, цикл нагружения – симметричный. При таком цикле изменения напряжений, допускаемое напряжение определяется по формулам: 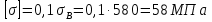 (37) (37)где:  предельная несущая способность материала. предельная несущая способность материала.Материалом вала назначим высокоуглеродистую сталь 45, для которой  (обработка стали: нормализация и улучшение). (обработка стали: нормализация и улучшение). 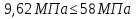 Неравенство прочности выполняется, значит, выбранный материал подходит. Определим коэффициент запаса: 
Для ограничения упругого мертвого хода:  мм, (38) мм, (38)где 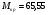 Н*мм – крутящий момент, Н*мм – крутящий момент,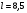 мм – рабочая длина вала, мм – рабочая длина вала, МПа – модуль упругости при сдвиге, МПа – модуль упругости при сдвиге,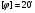 - допускаемое значение угла закручивания вала - допускаемое значение угла закручивания валаС учётом проведённых расчетов и значения диаметра вала выбранного двигателя, назначаем диаметры валов из стандартного ряда по ГОСТ 12081-72:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
