Роль статистики в бизнесе. Лекция+1+ВВЕДЕНИЕ+РОЛЬ+СТАТИСТИКИ+В+БИЗНЕСЕ. Тема 1 введение роль статистики в бизнесе 1 Статистические методы в управлении Статистика
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
ТЕМА 3 АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ 3.1 Абсолютные величины Статистическая величина – это количественная оценка свойств изучаемого явления. Статистика при помощи статистических показателей характеризует размер изучаемых явлений, их способности, закономерности развития. Статистические показатели характеризуются по ряду признаков. Статистический признак – это свойство, качество, отличительная черта единицы совокупности. Основная классификация признаков в статистикие
Статистические величины подразделяются на: абсолютные; относительные; средние. Абсолютные величины отражающие уровень развития какого-либо явления (например, величина экспорта/импорта i-го товара в j-ю страну). Абсолютные величины обозначаются – Х, а их общее количество статистической совокупности – N.  Абсолютные величины  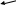   суммарные (характеризуют итоговые значения признака по определенной совокупности объектов статистического наблюдения) например, экспорт Казахстана за 2000-2010 годы индивидуальные (характеризуют размеры признака у отдельных единиц совокупности) например, экспорт Казахстана 2010 года   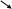 моментные отражает уровень развития на определенную дату (например: экспортная цена на нефть) ∑≠  интервальные отражает уровень развития явления за определенный интервал времени (например: величина экспорта за месяц, квартал)   «+» «-» (убытки, убыль, потери) Широко распространены в таможенной статистике следующие виды единиц измерения: натуральные, подразделяющиеся на простые (например, штуки, тонны, метры) и сложные (составные), представляющие собой комбинацию двух разноименных величин (например, киловатт-час); условно-натуральные (например, алкогольные напитки учитываются в дкл 100% спирта, а различные виды топлива соизмеряют по условному топливу с теплотворной способностью 7000 ккал/кг или 29,3 МДж/кг); стоимостные, позволяющие соизмерить в денежной форме товары, которые нельзя соизмерить в натуральной форме (тенге, доллары США и т.д.). Количество единиц с одинаковым значением признака обозначается f и называется частота. Очевидно, что суммируя число всех величин с одинаковыми значениями признака, получаем N, то есть: 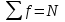 3.2 Относительные величины Относительная величина – это результат деления (сравнения) двух абсолютных величин.  сравниваемый показатель      показывает во сколько раз   показатель, с которым производится сравнение 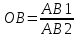 Относительные показатели выражаются в следующих формах: коэффициентная (база сравнения 1); процентная (база сравнения 100); промилльная (база сравнения 1000). Выбор той или иной формы относительной величины зависти от ее абсолютного значения: если сравниваемая величина больше базы сравнения в 2 раза и более, то выбирают форму коэффициента; если относительная величина близка к единице, то, как правило, ее выражают в процентах (например, сравнив величины экспорта Казахстана в 2016 и 2015 годах, которые составили 304,5 и 243,6 млрд. долл. Соответственно, можно сказать, что экспорт в 2016 году составляет 125% от 2015 года [304,5/243,6*100%]; если относительная величина значительно меньше единицы (близка к нулю), ее выражают в промилле (например, в 2016 году Казахстан экспортировал в страны-СНГ всего 4142 тыс. т нефтепродуктов, в том числе в Грузию 10,7 тыс. т, что составляет 0,0026 [10,7/4142], или 2,6% от всего экспорта нефтепродуктов в страны СНГ). Различают относительные величины: динамики; структуры; координации; сравнения; интенсивности. Относительная величина динамики характеризует изменение какого-либо явления во времени. Она представляет собой отношение значений одной и той же абсолютной величины в разные периоды времени 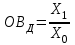 где, цифры означают: 1 – отчетный или анализируемый период, 0 – прошлый или базисный период. Критериальным значением относительного показателя динамики служит единица (100%), то: если ОВД 1, то имеет место рост (увеличение) явления во времени; если ОВД = 1 – стабильность; если ОВД < 1 – наблюдается спад (уменьшение) явления. Разновидностями относительной величины динамики являются относительная величина планового задания и выполнения плана. Относительная величина планового задания – это отношение уровня, запланированного на предстоящий период, к уровню показателя, достигнутого в предыдущем периоде. 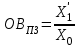 где, 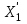 – планируемое значение; – планируемое значение; 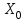 – базисное значение признака. – базисное значение признака.Например, таможенное управление перечислило в государственный бюджет в 2016 году 160 млрд. тенге, а на следующий год запланировали перечислить 200 млрд. тенге, значит ОВпз = 200/160 = 1,25, то есть плановое задание для таможенного управления на 2016 год составляет 125% от предыдущего года. Относительная величина выполнения плана – это отношение фактически достигнутого уровня в текущем периоде к уровню планируемого показателя на этот же период:  Например, на январь-ноябрь 2016 года таможенные органы запланировали перечислить в республиканский бюджет 1,955 трлн. тенге, но фактически перечислили 2,59 трлн. тенге, ОВВП = 2,59/1,955 = 1,325, или 132,5%, то есть плановое задание выполнили на 132,5%. Относительная величина структуры (доля) – это отношение какой-либо части объекта (совокупности) ко всему объекту. 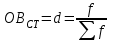 Относительная величина координации – это отношение какой-либо части объекта к другой его части, принятой за основу.  Например, импорт Казахстана в 2016 году составил 163,9 млн. долл., а экспорт 304,5 млн. долл., тогда сравнив его с экспортом, получим:  = 163,9/304,5 = 0,538, который показывает соотношение между двумя составными частями внешнеторгового оборота, то есть величина импорта Казахстана в 2016 году составляет 53,8% от величины экспорта. = 163,9/304,5 = 0,538, который показывает соотношение между двумя составными частями внешнеторгового оборота, то есть величина импорта Казахстана в 2016 году составляет 53,8% от величины экспорта.Относительная величина сравнения – характеризует отношение одноименных показателей, соответствующих одному и тому же периоду или моменту времени, но к различным объектам или территориям.  где, А,Б – сравниваемые объекты. Например, экспорт США составил 904,393 млрд. долл., а экспорт Казахстана 243,569 млрд. долл. ОВС = 904,393/243,569 = 3,71 ОВС =243,569/904,393 = 0,26 Относительная величина интенсивности – характеризует степень насыщенности или развития данного явления в определенной среде, является именованным показателем.  где, 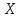 – один признак объекта; – один признак объекта; 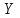 – другой признак этого же объекта. – другой признак этого же объекта.Например, Среднегодовая численность населения Республики Казахстан в 2016 г. составила 17194055 человек, число родившихся – 400694 человек, число умерших – 131231человек Определим коэффициент рождаемости: 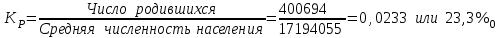 Таким образом, рождаемость детей в Казахстане в расчёте на 1000 человек населения составляла в 2016 году 23,3 человека. ТЕМА 4 ОПИСАНИЕ ДАННЫХ: ОБОБЩАЮЩИЕ ПОКАЗАТЕЛИ 4.1 Виды средних величин и порядок их вычисления Одна из основных задач бизнес-статистики состоит в надлежащей обработке набора данных (информации). У бизнес-статистики есть много других задач: получение и хранение информации, выработка различных прогнозов, оценка их достоверности и т.д. ни одна из этих целей не достижима без обработки данных. Поэтому первым, чем стоит заняться – это статистическими методами обработки информации. В сложных ситуациях один из самых эффективных способов «увидеть всю картину» заключается в обобщении, т.е. использовании одного или нескольких отобранных или рассчитанных значений для характеристики набора данных. Одна из целей статистики состоит в том, чтобы свести набор данных к одному числу (или двум, или нескольким), которое выражает наиболее фундаментальные свойства данных. Такой представленный одним числом показатель называется типическим значением, или центром. Существуют три вида такой обобщающей меры. 1. Среднее, которое можно вычислять только для имеющих содержательный смысл чисел (для количественных данных). 2. Медиана, или серединная точка, которую можно вычислять как для упорядоченных категорий (порядковые данные), так и для чисел. 3. Мода, или наиболее часто встречающаяся категория, которую можно вычислять для неупорядоченных категорий (для номинальных данных), для упорядоченных категорий и для чисел. Средняя величина – обобщающий показатель, выражающий типичные размеры количественно варьирующихся признаков качественно однородных явлений. Средняя величина характеризует общий уровень этого признака, отнесенный к единице этой совокупности.           взвешенные простые степенные - средняя арифметическая; - средняя гармоническая; - средняя геометрическая; - средняя квадратическая Средние величины структурные - мода; - медиана Общая формула степенной средней имеет вид:  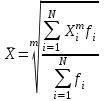 где, 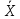 –степенная средняя; –степенная средняя; – меняющиеся величины признака (варианты); – меняющиеся величины признака (варианты); – число вариант (наблюдений); – число вариант (наблюдений);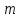 – показатель степени средней; – показатель степени средней; 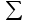 –знак суммирования; –знак суммирования; – частоты (весы) соответствующих вариантов. – частоты (весы) соответствующих вариантов.Правило: при 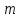 = 1 получаем среднюю арифметическую; = 1 получаем среднюю арифметическую;при 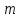 = -1 – среднюю гармоническую; = -1 – среднюю гармоническую;при 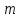 = 0 – среднюю геометрическую; = 0 – среднюю геометрическую;при 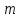 = 2 – среднюю квадратическую; = 2 – среднюю квадратическую;Чем выше показатель степени m, тем больше значение средней величины (если индивидуальные значения признака варьируют). В итоге, можно построить следующее соотношение, которое называется правилом мажорантности средних:  ≤ ≤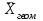 ≤ ≤ ≤ ≤ Средняя арифмитическая- самый распространённый вид средний. Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объём признака в совокупности сохраняется неизменным.Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности. Исходя из определения, формула средней арифметической постой величины имеет вид:  Пример. Вычислить среднюю заработную плату работников таможенного поста, где заняты 5 человек: 45000 тг, 50000 тг, 55000 тг, 60000 тг,65000 тг. При расчёте средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчёт средней величины производится по сгруппированным данным. В этом случае речь идёт об использовании средней арифметической взвешенной, которая имеет вид:  где, i - число групп. Например. Рассчитать, среднее число оформленных ГДТ за день, согласно исходной информации таблицы. Таблица – Распределение дней работника таможни по числу оформленных ГДТ в марте
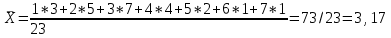 (оформленных работником, за день ГТД). Если при группировке значения осредняемого признака заданы интервалами, то при расчёте средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, то есть исходят из предположения о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспортным путём исходя из сущности, свойств признака и совокупности. При отсутствии возможности экспортной оценки значения признака в открытых интервалах, для нахождения недостающей границы открытого интервала применяют размах (разность между значениями конца и начала интервала) соседнего интервала (принцип «соседа»). Например. Рассчитать среднюю величину таможенной стоимости товара. Таблица – Распределение товаров по величине таможенной стоимости.
По условным данным можно минимальной величиной таможенной стоимости считать 0 тыс.долл., тогда первый интервал будет от 0 до 5 тыс.долл., а максимальную величину определить затруднительно, поэтому воспользуемся принципом «соседа» - интервал будет от 30 до 45 тыс.долл. Средняя величина таможенной стоимости равна:  тыс. дол. тыс. дол.Средняя арифметическая величина обладает свойствами: Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю. Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшиться во столько же раз. Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то средняя величина возрастёт или уменьшится на это же число. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа. Среднюю называют обратной средней арифметической – средняя гармоническая. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Её формулу можно вывести из базовой формулы, подставив m=-1: 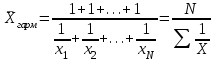 Вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая – со скоростью 100км/ч, вторая – 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость: 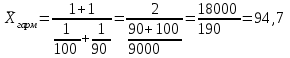 км/ч км/чВ статической практике чаще всего используется гармоническая взвешенная, формула которой имеет вид: 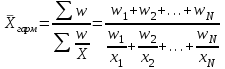 где, 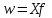 Данная формула используется в тех случаях, когда веса (или объёмы явлений) по каждому признаку не равны. В исходном соотношении для расчёта средней известен числитель, но неизвестен знаменатель. Например.Необходимо узнать среднюю цену реализованных товаров:
При расчёте средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идёт о разных товарах), но известны суммы реализаций этих различных товаров. 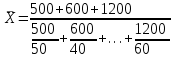 Среднегеометрическая величина даёт возможность сохранить в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Для определения средней геометрической простой применяется формула: 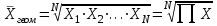 Для определения средней геометрической взвешенной применяется формула:  Среднегеометрические величины наиболее часто используются: при анализе темпов роста экономических показателей; для определения равноудалённой величины от максимального и минимального значений признака (например между 100 и 10000000). Например. Страховая компания заключает договоры на оказание клиентам различных услуг медицинского страхования. В зависимости от категории медицинского учреждения, ассортимента услуг, конкретного рискового случая страховая сумма может измениться от 100 до 10 000 долл. в год. 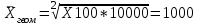 Главной сферой применения средней квадратической в силу пятого свойства средней арифметической величины является измерение вариации признака в совокупности. Средние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической. Формула простой среднейквадратической:  Формула взвешенной средней квадратической: 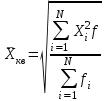 Например, диаметры корзин подсолнуха представлены в таблице, мм
Средняя величина диаметра равна 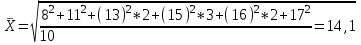 мм ммМода и медиана - структурные и описательные средние. Структурные средние применяются для изучения внутреннего строения и структуры рядов распределения значений признака. В практике эти величины применяются при определении покупательского спроса на отдельные товары, при определении качества товаров, при регистрации цен и др., т.е. в основном в маркетинговой деятельности. Мода – это есть варианта, у которой частота (вес) наибольший. Модальная величина в дискретном ряду находится просто – по наибольшей частоте. Например, организация регистрирует причину брака каждый раз при появлении изделия недопустимого качества.
Мо = блок питания Несколько сложнее определение моды в интервальном ряду. В этих случаях необходимо моду находить расчетным путем по формуле: 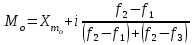 где, 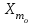 – нижняя граница модального интервала – нижняя граница модального интервала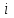 – разность между верхней и нижней границей модального интервала – разность между верхней и нижней границей модального интервала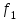 – частота интервала, предшествующая модальному – частота интервала, предшествующая модальному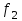 – частота модального интервала – частота модального интервала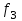 – частота интервала, следующего за модальным – частота интервала, следующего за модальнымПример, на основании группировочных данных о торговой площади магазинов произведем расчет моды из интервального ряда Группировочные данные по торговой площади магазинов
 кв.м. кв.м.Следовательно, из этой группы больше всего магазинов имеют торговую площадь 145,8 кв.м. Медианой называется серединная варианта упорядоченного вариационного ряда, расположенного в возрастающем или убывающем порядке. Если ряд нечетный – медиана является центральным членом и делит вариационный ряд пополам.  161 Пример, А) Дан нечетный вариационный ряд выработки продукции одним работником, шт.: 156 158 160 166 168 172 Центральным членом (медианой) данного ряда является выработка продукции одним работником – 161 шт.. Если ряд четный – медиана определяется следующим образом: серединные два члена вариационного ряда складываются и делятся пополам. Б) Дан четный вариационный ряд выработки продукции одним работником, шт.: 155 156 158 160 161 166 168 172  Порядковый номер медианы определяется по формуле: 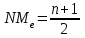 Пример, Необходимо дать среднюю характеристику среднего дохода группы людей, насчитывающей 100человек, из которых 99 имеют доходы в интервале от 100 до 200 долл. в месяц, а месячные доходы последнего составляют 50000 долл. в месяц. №п/п 1 2 3 4 … 50 51 … 99 100 доход (долл.) 100 104 104 107 .. 162 164 … 200 50000  т.е. медиана равная в данном случае 163 долл. позволяет дать объективную оценку уровня дохода 99% данной совокупности людей. Расчет медианы интервального ряда производится по формуле:  где,  – нижняя граница медианного интервала – нижняя граница медианного интервала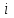 – разность между верхней и нижней границей медианного интервала – разность между верхней и нижней границей медианного интервала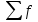 – сумма частот интервального ряда – сумма частот интервального ряда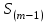 – сумма накопленных частот в интервалах предшествующих медианному – сумма накопленных частот в интервалах предшествующих медианному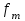 – частота медианного интервала – частота медианного интервалаПример, В интервальном ряду даны группы семей по среднемесячному доходу на 1 человека. Определить медиана.
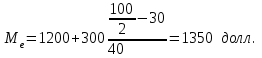 Следовательно, 50% семей имеют доход на одного человека не более 1350 долл., а 50% имеют доход на одного человека более 1350 долл. Свойство медианы: сумма абсолютных величин линейных отклонений от 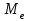 минимальна. минимальна.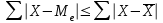 Пример, Филиалы торговой фирмы «Элегант» расположены на расстоянии 10, 30, 70, 90, 100 км от нее. Где построить склад фирмы для оптимального снабжения филиалов?
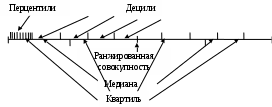
 =60 км. =60 км.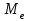 =70 км =70 кмТ.о. оптимальным вариантом является медианное расстояние 70 км, т.к. 150<160 км на 10 км. 4.2 Вычисление границ процентных и долевых сегментов Медиана определяет середину (по количеству точек) совокупности. Однако часто возникает необходимость найти другие разбиения, например, такое, что левее границы разбиения находится 90%-ов значений, а правее 10%-ов. Подобные задачи можно решать с помощью функций квартиль, дециль и персентиль. Квартиль представляет собой значение признака, делящее ранжированную совокупность на 4 равновеликие части.     Кваритиль (Q)    Q2=Мe Q3 (верхний) определяющий ¼ часть совокупности с наибольшими значениями признака Q1 (нижний) определяющий ¼ часть совокупности с наименьшими значениями признака   Q1 – mах значение Х для первых 25% единиц образования, но min для последних 75% 25% от 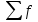 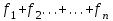 =25% выборки =25% выборкиНапример, №п/п 3 8 15 20 25  1 5 1 3 6 1 5 1 3 625% от 16 объектов = 4 Q1=8 Q3=25 Д  ля расчета квартилей по интервальному вариационному ряду используют формулы: 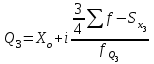 где,  – нижняя граница квартильных интервалов – нижняя граница квартильных интервалов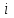 – величина интервала – величина интервала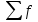 – сумма частот – сумма частот 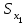 – накопленная частота интервала, предшествующего нижнему квартилю – накопленная частота интервала, предшествующего нижнему квартилю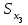 – накопленная частота интервала, предшествующего верхнему квартилю – накопленная частота интервала, предшествующего верхнему квартилю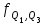 – частоты квартильного интервала – частоты квартильного интервалаДециль – делит совокупность на десять равных частей. Формулы для децелей в интервальном вариационном ряду записываются следующим образом:  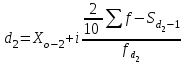 Дан интервальный ряд распределения 50 работников по росту. Определить верхний и нижний квартиль и первых два дециля.
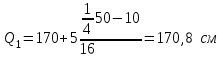 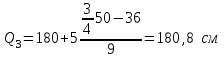  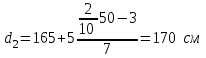  |