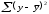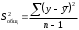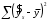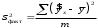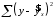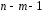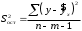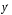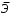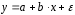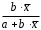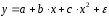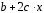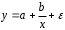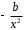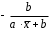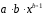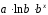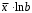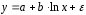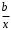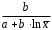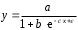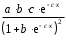Роль статистики в бизнесе. Лекция+1+ВВЕДЕНИЕ+РОЛЬ+СТАТИСТИКИ+В+БИЗНЕСЕ. Тема 1 введение роль статистики в бизнесе 1 Статистические методы в управлении Статистика
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
10.2 Линейная модель парной регрессии и корреляции Рассмотрим простейшую модель парной регрессии – линейную регрессию. Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида 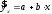 или или 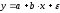 . . Уравнение вида 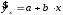 позволяет по заданным значениям фактора позволяет по заданным значениям фактора 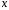 находить теоретические значения результативного признака, подставляя в него фактические значения фактора находить теоретические значения результативного признака, подставляя в него фактические значения фактора 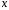 . .Построение линейной регрессии сводится к оценке ее параметров – 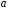 и и 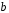 . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 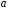 и и 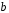 , при которых сумма квадратов отклонений фактических значений результативного признака , при которых сумма квадратов отклонений фактических значений результативного признака 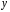 от теоретических от теоретических 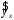 минимальна: минимальна: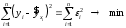 Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рисунок 2): 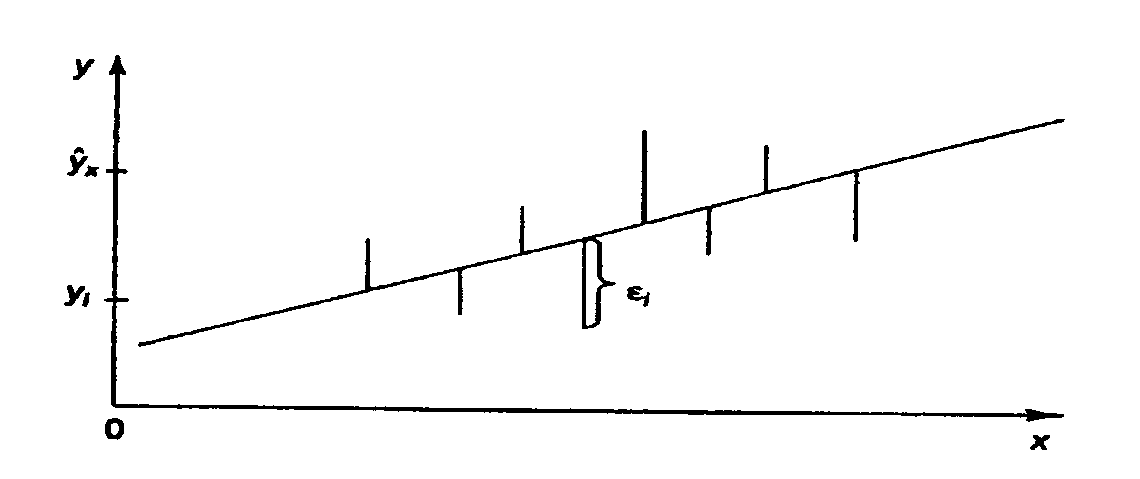 Рисунок 2 – Линия регрессии с минимальной дисперсией остатков Как известно из курса математического анализа, чтобы найти минимум функции (2), надо вычислить частные производные по каждому из параметров 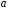 и и 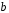 и приравнять их к нулю. Обозначим и приравнять их к нулю. Обозначим 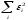 через через  , тогда: , тогда: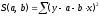 . .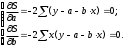 После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров 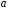 и и 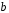 : : Решая систему уравнений (4), найдем искомые оценки параметров 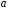 и и 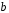 . Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (4): . Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (4):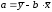 , , 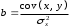 , , где 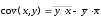 – ковариация признаков – ковариация признаков 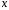 и и 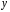 , ,  – дисперсия признака – дисперсия признака 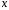 и и 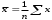 , , 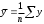 , , 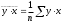 , ,  . .Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности. Параметр 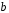 называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу его измерения. называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу его измерения.Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях. Формально 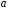 – значение – значение 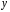 при при 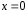 . Если признак-фактор . Если признак-фактор 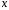 не может иметь нулевого значения, то вышеуказанная трактовка свободного члена не может иметь нулевого значения, то вышеуказанная трактовка свободного члена 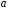 не имеет смысла, т.е. параметр не имеет смысла, т.е. параметр 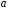 может не иметь экономического содержания. может не иметь экономического содержания. Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 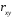 , который можно рассчитать по следующим формулам: , который можно рассчитать по следующим формулам: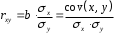 Линейный коэффициент корреляции находится в пределах: 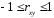 . Чем ближе абсолютное значение . Чем ближе абсолютное значение 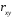 к единице, тем сильнее линейная связь между факторами (при к единице, тем сильнее линейная связь между факторами (при 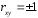 имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной. имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 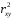 , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака 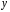 , объясняемую регрессией, в общей дисперсии результативного признака: , объясняемую регрессией, в общей дисперсии результативного признака: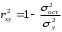 , , где 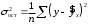 , , 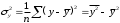 . .Соответственно величина 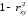 характеризует долю дисперсии характеризует долю дисперсии 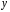 , вызванную влиянием остальных, не учтенных в модели, факторов. , вызванную влиянием остальных, не учтенных в модели, факторов.После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации: 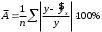 . . Средняя ошибка аппроксимации не должна превышать 8–10%. Оценка значимости уравнения регрессии в целом производится на основе 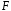 -критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели. -критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной 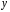 от среднего значения от среднего значения  раскладывается на две части – «объясненную» и «необъясненную»: раскладывается на две части – «объясненную» и «необъясненную»: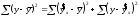 где 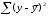 – общая сумма квадратов отклонений; – общая сумма квадратов отклонений; 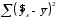 – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); 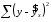 – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов. – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.Схема дисперсионного анализа имеет вид, представленный в таблице 1 (  – число наблюдений, – число наблюдений, 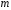 – число параметров при переменной – число параметров при переменной 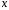 ). ).Таблица 1 – Дисперсионный анализ
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину 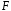 -критерия Фишера: -критерия Фишера: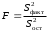 Фактическое значение 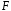 -критерия Фишера (9) сравнивается с табличным значением -критерия Фишера (9) сравнивается с табличным значением  при уровне значимости при уровне значимости 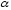 и степенях свободы и степенях свободы 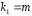 и и 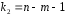 . При этом, если фактическое значение . При этом, если фактическое значение 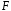 -критерия больше табличного, то признается статистическая значимость уравнения в целом. -критерия больше табличного, то признается статистическая значимость уравнения в целом.Для парной линейной регрессии 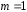 , поэтому , поэтому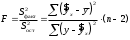 . . Величина 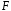 -критерия связана с коэффициентом детерминации -критерия связана с коэффициентом детерминации 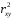 , и ее можно рассчитать по следующей формуле: , и ее можно рассчитать по следующей формуле: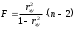 . . В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: 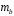 и и 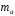 . .Стандартная ошибка коэффициента регрессии определяется по формуле: 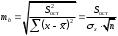 , , где 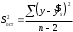 – остаточная дисперсия на одну степень свободы. – остаточная дисперсия на одну степень свободы.Величина стандартной ошибки совместно с 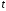 -распределением Стьюдента при -распределением Стьюдента при 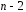 степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала. степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение 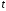 -критерия Стьюдента: -критерия Стьюдента: 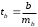 которое затем сравнивается с табличным значением при определенном уровне значимости которое затем сравнивается с табличным значением при определенном уровне значимости 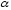 и числе степеней свободы и числе степеней свободы 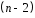 . Доверительный интервал для коэффициента регрессии определяется как . Доверительный интервал для коэффициента регрессии определяется как 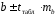 . Поскольку знак коэффициента регрессии указывает на рост результативного признака . Поскольку знак коэффициента регрессии указывает на рост результативного признака 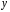 при увеличении признака-фактора при увеличении признака-фактора 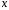 ( (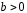 ), уменьшение результативного признака при увеличении признака-фактора ( ), уменьшение результативного признака при увеличении признака-фактора (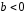 ) или его независимость от независимой переменной ( ) или его независимость от независимой переменной (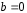 ) (рисунок 3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, ) (рисунок 3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например,  . Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть. . Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.Стандартная ошибка параметра 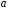 определяется по формуле: определяется по формуле: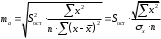 . . 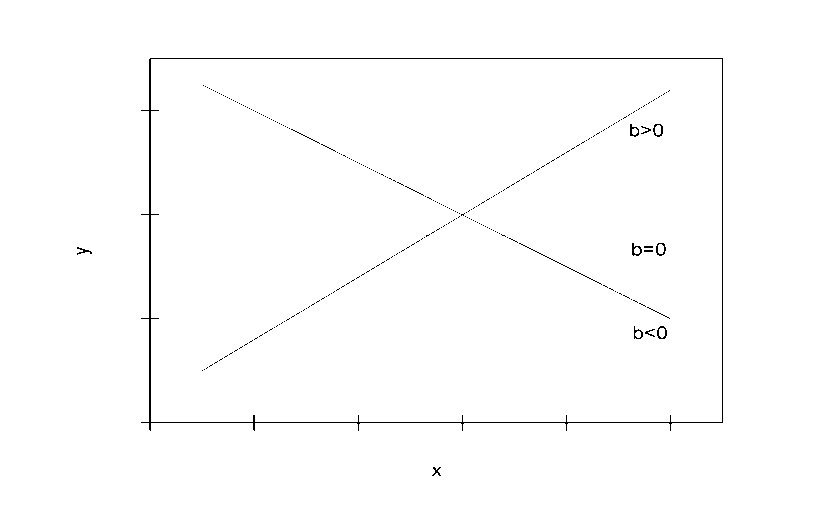 Рисунок 3 – Наклон линии регрессии в зависимости от значения параметра 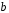 . .Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется 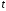 -критерий: -критерий: 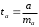 , его величина сравнивается с табличным значением при , его величина сравнивается с табличным значением при 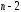 степенях свободы. степенях свободы.Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции 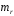 : :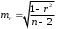 Фактическое значение 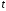 -критерия Стьюдента определяется как -критерия Стьюдента определяется как 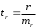 . .Существует связь между 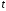 -критерием Стьюдента и -критерием Стьюдента и 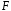 -критерием Фишера: -критерием Фишера: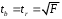 В прогнозных расчетах по уравнению регрессии определяется предсказываемое 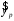 значение как точечный прогноз значение как точечный прогноз 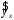 при при 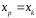 , т.е. путем подстановки в уравнение регрессии , т.е. путем подстановки в уравнение регрессии 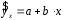 соответствующего значения соответствующего значения 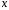 . Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки . Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки 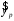 , т.е. , т.е. 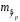 , и соответственно интервальной оценкой прогнозного значения , и соответственно интервальной оценкой прогнозного значения 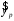 : :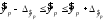 где 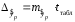 , а , а 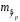 – средняя ошибка прогнозируемого индивидуального значения: – средняя ошибка прогнозируемого индивидуального значения: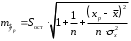 . . 10.3 Нелинейные модели парной регрессии и корреляции Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например – полиномы различных степеней – 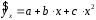 , , 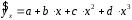 ; ;– равносторонняя гипербола – 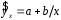 ; ;– полулогарифмическая функция – 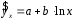 . .Регрессии, нелинейные по оцениваемым параметрам, например – степенная – 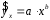 ; ;– показательная – 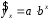 ; ;– экспоненциальная – 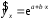 . .Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции. Парабола второй степени 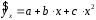 приводится к линейному виду с помощью замены: приводится к линейному виду с помощью замены:  . В результате приходим к двухфакторному уравнению . В результате приходим к двухфакторному уравнению 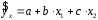 , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений: , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений: А после обратной замены переменных получим 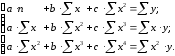 Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. Равносторонняя гипербола 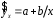 может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы (например, кривая А.В. Филлипса), расходов на непродовольственные товары от доходов или общей суммы расходов (например, кривые Э. Энгеля) и в других случаях. Гипербола приводится к линейному уравнению простой заменой: может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы (например, кривая А.В. Филлипса), расходов на непродовольственные товары от доходов или общей суммы расходов (например, кривые Э. Энгеля) и в других случаях. Гипербола приводится к линейному уравнению простой заменой: 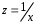 . Система линейных уравнений при применении МНК будет выглядеть следующим образом: . Система линейных уравнений при применении МНК будет выглядеть следующим образом: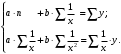 Аналогичным образом приводятся к линейному виду зависимости 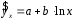 , , 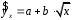 и другие. и другие.Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся). К внутренне линейным моделям относятся, например, степенная функция – 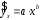 , показательная – , показательная – 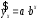 , экспоненциальная – , экспоненциальная –  , логистическая – , логистическая –  , обратная – , обратная – 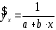 . .К внутренне нелинейным моделям можно, например, отнести следующие модели: 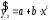 , , 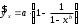 . .Среди нелинейных моделей наиболее часто используется степенная функция 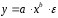 , которая приводится к линейному виду логарифмированием: , которая приводится к линейному виду логарифмированием: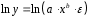 ; ;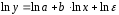 ; ; , ,где 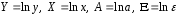 . Т.е. МНК мы применяем для преобразованных данных: . Т.е. МНК мы применяем для преобразованных данных: а затем потенцированием находим искомое уравнение. Широкое использование степенной функции связано с тем, что параметр 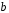 в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид: в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид: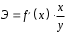 . . Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора 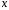 , то обычно рассчитывается средний коэффициент эластичности: , то обычно рассчитывается средний коэффициент эластичности: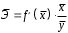 . . Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах. Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции: 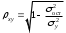 , , где 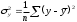 – общая дисперсия результативного признака – общая дисперсия результативного признака 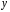 , , 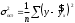 – остаточная дисперсия. – остаточная дисперсия.Величина данного показателя находится в пределах: 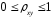 . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии. . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака 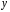 , объясняемую регрессией, в общей дисперсии результативного признака: , объясняемую регрессией, в общей дисперсии результативного признака: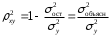 , , т.е. имеет тот же смысл, что и в линейной регрессии; 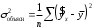 . .Индекс детерминации 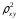 можно сравнивать с коэффициентом детерминации можно сравнивать с коэффициентом детерминации 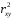 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина 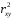 меньше меньше 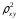 . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.Индекс детерминации используется для проверки существенности в целом уравнения регрессии по 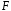 -критерию Фишера: -критерию Фишера: , , где 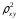 – индекс детерминации, – индекс детерминации,  – число наблюдений, – число наблюдений, 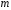 – число параметров при переменной – число параметров при переменной 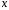 . Фактическое значение . Фактическое значение 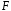 -критерия (1.23) сравнивается с табличным при уровне значимости -критерия (1.23) сравнивается с табличным при уровне значимости 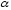 и числе степеней свободы и числе степеней свободы 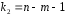 (для остаточной суммы квадратов) и (для остаточной суммы квадратов) и 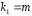 (для факторной суммы квадратов). (для факторной суммы квадратов).О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае, вычисляется по формуле (8). ЛЕКЦИЯ 11 ИНДЕКСЫ И ИХ ИСПОЛЬЗОВАНИЕ В БИЗНЕС-СТАТИСТИКЕ
11.1 Индексы, их общая характеристика и сфера применения Индекс – это относительная величина, показывающая во сколько раз уровень изучаемого явления в данных условиях отличается от уровня этого же явления в других условиях. Различие условий проявляется во времени, пространстве, а также в выборе в качестве базы сравнения какого-либо условного уровня. Индексы выражаются относительными числами (К, %, %0). Индексы классифицируются: по степени охвата: индивидуальные индексы; общий (сводный) индекс. по базе сравнения: динамические: базисные; цепные; б) территориальные. по виду весов (соизмерителей): с постоянными весами; с переменными весами. по форме построения: агрегатные; средние: среднеарифметические; среднегармонические. по характеру объекта исследования: индексы количественных (объемных) показателей; индексы качественных показателей. по составу явления: индексы переменного состава называют отношение двух средних уровней; индексы фиксированного (постоянного) состава есть средний из индивидуальных индексов. по периоду исчисления: годовые; квартальные; месячные; недельные. 11.2 Индивидуальные индексы Индивидуальные индексы (i) служат для характеристики изменения отдельных элементов сложного явления. Индивидуальные индексы получают при сравнении уровня изучаемого явления в данных условиях с уровнем этого же явления в других условиях. Индивидуальные индексы: индивидуальный индекс физического объема продукции отражает изменение выпуска продукции: 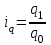 где 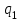 и и 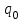 – количество продукции данного вида в натуральном выражении в отчетном и базисном периодах. – количество продукции данного вида в натуральном выражении в отчетном и базисном периодах.индивидуальный индекс цен характеризует изменение цен по одному виду продукции и определяется по формуле: 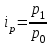 где p1 и p0 – цена за единицу продукции в отчетном и базисном периодах. индивидуальный индекс себестоимости характеризует изменение себестоимости по одному виду продукции и определяется по формуле: 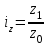 где 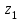 и и 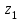 – себестоимость за единицу продукции в отчетном и базисном периодах. – себестоимость за единицу продукции в отчетном и базисном периодах.индивидуальный индекс производительности труда характеризует изменение производительности труда по одному виду продукции и определяется по формуле: 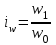 где 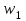 и и 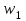 – производительность труда за единицу продукции в отчетном и базисном периодах. – производительность труда за единицу продукции в отчетном и базисном периодах.индивидуальный индекс товарооборота характеризует изменение товарооборота по одному виду продукции и определяется по формуле: 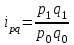 где 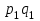 и и 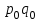 – производительность труда за единицу продукции в отчетном и базисном периодах. – производительность труда за единицу продукции в отчетном и базисном периодах.индивидуальный индекс затрат на производство характеризует изменение затрат на производство по одному виду продукции и определяется по формуле: 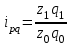 где 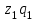 и и 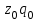 – затрат на производство за единицу продукции в отчетном и базисном периодах. – затрат на производство за единицу продукции в отчетном и базисном периодах.11.3 Сводная форма индексов Сводными индексами называются относительные числа, характеризующие соотношения между такими совокупностями величин экономических явлений, которые непосредственно в своей натуральной форме несоизмеримы. Основной формой сводных индексов является агрегатная. Агрегатный индекс – это сложный относительный показатель, в котором непосредственно сравниваются суммы произведений двух величин. Одна из них изменяется – это индексируемая величина, а другая остается неизменной и в числителе, и в знаменателе – это вес индекса. Индексируемой величиной является признак, изменение которого изучается. Вес индекса – это величина, служащая для целей соизмерения индексируемых величин. При выборе веса индекса придерживаются следующих правил: 1) если строится индекс количественного показателя, то веса берутся за базисный период; 2) при построении индекса качественного показателя используются веса отчетного периода. Общие (сводные индексы): общий индекс физического объема продукции: 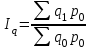 где 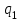 и и 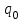 – количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; – количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; 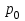 – цена единицы продукции (отдельного вида) в базисном периоде. – цена единицы продукции (отдельного вида) в базисном периоде.общий индекс цен: Для характеристики среднего изменения цен на потребительские товары используют индекс цен, предложенный Э. Ласпейресом (индекс Ласпейреса): 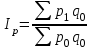 где 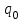 – потребительская корзина (базовый период); – потребительская корзина (базовый период); 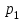 и и 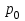 - соответственно цены отчетного и базисного периодов. - соответственно цены отчетного и базисного периодов.Если количество набора продуктов принимается на уровне отчетного периода ( 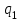 ), то в этом случае индекс цен именуется индексом Пааше: ), то в этом случае индекс цен именуется индексом Пааше: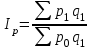 общий индекс стоимости: 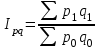 общий индекс себестоимости продукции: 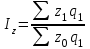 общий индекс издержек производства: 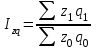 ТЕМА 13 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ЭФФЕКТИВНОСТИ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ 13.1 Реализация решений 13.2 Организация и контроль выполнения решений 132.3 Оценка эффективности решений 13.1 Организация должна иметь механизм реализации принимаемых решений и состоять из следующих процедур: - разработка плана реализации решения; управление реализацией; контроль выполнения решения; оценка результатов реализации. Выделяют две группы людей: те, кто готовит решение (Р) – имеет преимущественно аналитическо-логический стиль мышления (АЛ) те, кто его реализуют (Н) – имеет интуитивно-синтетический стиль мышления (ИС) Люди из первой группы должны определить: - что нужно сделать; - как и кому надо это делать; - что следует предпринять, когда есть четкие указания по двум предыдущим вопросам, но решение не реализуется. Основные причины неудач при реализации решений: - руководство организации слабо знакомо с терминологией и логикой теории принятия решений; - в ряде случаев набор альтернатив, предоставляемых руководителям для выбора, не соответствует их запросам (неточно понятная цель, неточный критерий, наличие неутонченных, но важных факторов); - многие трудности возникают из-за того, что руководители среднего и нижнего уровней не имеют прав в выдаче разрешений на проведение анализа о деятельности подразделения, даже своего уровня иерархии. 13.2 Процесс организации выполнения решения включает три взаимосвязанных этапов: доведение задач до сознания исполнителей; подготовку исполнителей для выполнения задания; побуждение исполнителей к его добросовестному выполнению Заключительным этапом разработки и реализации решения является контроль Контроль – это одна из функций управления, представляющая собой процесс обеспечения достижения целей, поставленных организацией, обеспечения реализации принятых управленческих решений. Основная причина необходимости контроля – это неопределенность, являющаяся неотъемлемым элементом будущего и присущая любому управленческому решению, выполнение которого предполагается в будущем. Содержание контроля проявляется в выполняемых им функциям: диагностики состояния дел; ориентирования; стимулирования; корректировки действий; распространения передового опыта; осуществление авторского надзора Процесс контроля включает четыре стадии: 1) установление норм деятельности; 2) сбор данных о фактических результатах; 3) сравнение и оценка фактического и ожидаемого итогов выполнения; 4) разработка и реализация корректирующих действий 13.3 В теории принятия решений иногда под УР – понимается внутренняя мыслительная деятельность субъекта управления по разрешению проблемной ситуации. Управленческие действия – внешне наблюдаемые процессы деятельности управленческих работников по обеспечению выполнения УР. Эффективность – результат чего-либо Эффект – это достигаемый результат в его материальном, денежном, социальном и других выражениях. Соотношение эффекта и затрат характеризует эффективность какой-либо деятельности или явления. Эффективность – это относительный эффект, результативность процесса или операции, определяемый как отношение эффекта к затратам, обусловившим его появление. Эффективность деятельности организации складывается из эффективности УР, способности к производству качественной продукции, эффективности ее сбыта, имиджа и т.д. Эффективность УР – это ресурсная результативность, полученная по итогам разработки и реализации управленческих решений. Классификация Эффективности УР: организационная эффективность УР – это факт достижения организацией целей меньшим числом работников или за меньшее время; социальная эффективность УР – это факт достижения целей для большего числа работников с меньшими финансовыми затратами; экономическая эффективность УР – это соотношение стоимости прибавочного продукта, полученного в результате реализации УР, и затрат на его разработку и реализацию Эффективность УР зависит от: уровня неопределенности внешней среды; характера деятельности ЛПР К эффективным управленческим решениям относятся решения обоснованные, выполняемые и легко принимаемые к исполнению, а к неэффективности наоборот. В состав качественных показателей эффективности разработки УР могут быть включены: - своевременность предоставления проекта; степень научной обоснованности решений; многовариантность расчетов; применение технических средств; ориентация на изучение и использование прогрессивного отечественного и зарубежного опыта; расходы, связанные с разработкой проектов решений; численность занятых в разработке решений; стоимость и сроки реализации проектов и др. Количественная оценка эффективности УР во многом затруднена из-за специфических особенностей управленческого труда, которые заключаются в следующем: управленческий труд, преимущественно творческий, трудно поддающийся нормированию и учету из-за различных психофизиологических возможностей людей; фактические результаты, как затраты на реализацию конкретного решения, далеко не всегда можно учесть количественно из-за отсутствия соответствующей документации и т.д. |