Роль статистики в бизнесе. Лекция+1+ВВЕДЕНИЕ+РОЛЬ+СТАТИСТИКИ+В+БИЗНЕСЕ. Тема 1 введение роль статистики в бизнесе 1 Статистические методы в управлении Статистика
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
ТЕМА 5 ИЗМЕНЕНИЕ СТЕПЕНИ РАЗБРОСА: ДИСПЕРСИЯ И СТАНДАРТНОЕ ОТКЛОНЕНИЕ Абсолютные показатели вариации Чтобы дать представление о величине варьирующего признака недостаточно исчислить средний показатель. Кроме средней необходим показатель, характеризующий вариацию признака. Вариация – это изменение значения признака у отдельных единиц совокупности. Вариация обусловлена действием различных факторов на развитие отдельных единиц совокупности. Чем более разнообразно условие, тем больше его вариация. Степень близости индивидуальных значений признака (вариант) к средней измеряется рядом абсолютных, средних и относительных статистических показателей. К ним относятся: размах вариации; среднее линейное отклонение; дисперсия; среднее квадратическое отклонение; коэффициент вариации. Для всех показателей вариации общим является следующие: если показатель вариации близко к нулю (т.е. индивидуальные значения признака мало отличаются друг от друга), то средняя арифметическая будет надежной характеристикой данной совокупности; если же ряд распределения характеризуется значительным рассеиванием (величина показателя вариации сильно отличается от нуля, является большой), то средняя арифметическая будет ненадежной и ее практическое применение будет ограничено. Размах вариации – это разность между наибольшим и наименьшим значением признака в изучаемой совокупности:  Размах вариации не отражает отклонений всех значений признака – это его недостаток. Он исчисляется при контроле качества продукции для определения систематически действующих причин на производственный процесс. Для измерения отклонения каждой варианты от средней величины в ряду распределения или в группировке применяется среднее линейное отклонение 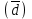 Среднее линейное отклонение 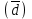 – это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней: – это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней: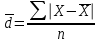 (простое) (простое)  (взвешенное) (взвешенное)Среднее линейное отклонение показывает, на сколько в среднем каждое значение признака отклоняется от средней величины. Эта величина всегда именованная и измеряется в тех же величинах, в которых даны статистические показатели. Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признаков совокупности. Средние линейные отклонения применяются на практике для анализа состава рабочих, ритмичности производства, равномерности поставок материалов и т.д. Наибольшее применение в практике статистических работ находит показатель – дисперсия признака или средний квадрат отклонений, или квадрат среднего квадратического отклонения (  ). ). Дисперсия (  ) – представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.: ) – представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.: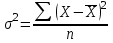 (простая) (простая) 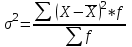 (взвешенная). (взвешенная).Корень квадратный из дисперсии представляет среднее квадратическое отклонение ( 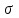 ): ):  . .Среднее квадратическое отклонение ( ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической  (простое) (простое) 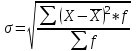 (взвешенное). (взвешенное).Среднее квадратическое отклонение дает обобщенную характеристику признака совокупности и показывает во сколько раз в среднем колеблется величина признака совокупности. Среднее квадратическое отклонение по величине всегда больше среднего линейного отклонения: 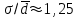 . .Среднее квадратическое отклонение используется: при определении значений ординат кривой нормального распределения; в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик; при оценке границ вариации признака в однородной совокупности. Среднее квадратическое отклонение является мерой надежности средней величины: чем оно меньше, тем точнее средняя арифметическая. Относительные показатели вариации Для сравнения вариации в разных совокупностях рассчитываются относительные показатели вариации. К ним относятся: 1. Коэффициент вариации – это отношение среднеквадратического отклонения к среднеарифметическому, рассчитывается в процентах: 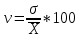 . .Коэффициент вариации позволяет судить об однородности совокупности: – < 17% – абсолютно однородная; – 17–33%% – достаточно однородная; – 35–40%% – недостаточно однородная; – 40–60%% – это говорит о большой колеблемости совокупности. 2. Коэффициент осцилляции – это отношение размаха вариации к средней, в процентах. Отражает относительную колеблемость крайних значений признака вокруг средней.  . .3. Линейный коэффициент вариации характеризует долю усредненного значения абсолютного отклонения от средней величины. 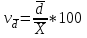 . .Виды дисперсии В зависимости от того, как представлена статистическая совокупность одним элементом или несколькими, различают следующие виды дисперсии: – общая дисперсия; – средняя внутригрупповая дисперсия; – межгрупповая дисперсия. Общая дисперсия( 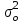 ) характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина определяется по формуле: ) характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина определяется по формуле: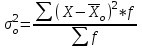 где 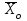 – общая средняя арифметическая всей исследуемой совокупности. – общая средняя арифметическая всей исследуемой совокупности.Средняя внутригрупповая дисперсия ( 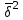 ) свидетельствует о случайной вариации, которая может возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от признака-фактора, положенного в основу группировки. Данная дисперсия рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным группам ( ) свидетельствует о случайной вариации, которая может возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от признака-фактора, положенного в основу группировки. Данная дисперсия рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным группам (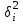 ), затем рассчитывается средняя внутригрупповая дисперсия ), затем рассчитывается средняя внутригрупповая дисперсия 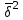 : :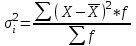   Межгрупповая дисперсия (  ) (дисперсия групповых средних) характеризует систематическую вариацию, т.е. различия в величине исследуемого признака, возникающие под влиянием признака-фактора, который положен в основу группировки. Эта дисперсия рассчитывается по формуле: ) (дисперсия групповых средних) характеризует систематическую вариацию, т.е. различия в величине исследуемого признака, возникающие под влиянием признака-фактора, который положен в основу группировки. Эта дисперсия рассчитывается по формуле: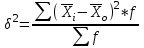 где 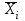 - средняя величина по отдельной группе. - средняя величина по отдельной группе.Все три вида дисперсии связаны между собой: общая дисперсия равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии: 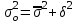 Данное соотношение отражает закон, который называют правилом сложения дисперсий. Общая дисперсия складывается из двух слагаемых, одно из которых измеряет вариацию внутри частей совокупности, а вторая – различия (вариацию) между этими частями (представленными средними). Благодаря правилу сложения дисперсий можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки. Отношение межгрупповой дисперсии к общей дает коэффициент детерминации: 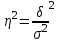 Он показывает, какая часть вариации результативного признака обусловлена факторными признаками, положенными в основание группировки.  - корреляционное эмпирическое отношение, которое показывает тесноту связи между результатом и факторным группировочным признаком. - корреляционное эмпирическое отношение, которое показывает тесноту связи между результатом и факторным группировочным признаком.Если 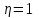 – связь между факторами полная, т.к. вариация результативного признака обусловлена факторным группировочным признаком. – связь между факторами полная, т.к. вариация результативного признака обусловлена факторным группировочным признаком.Если  – связь отсутствует. – связь отсутствует.ЛЕКЦИЯ 6 ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ 6.1 Понятие о выборочном наблюдении и его теоретические основы Выборочное наблюдение есть такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, затем отобранная часть изучается, а далее результаты распространяются на всю исходную совокупность. Цель выборочного наблюдения – по отобранной части единиц дать характеристику всей совокупности единиц. Генеральная совокупность – это совокупность, из которой производится отбор. Все обобщающие показатели данной совокупности называются генеральными. Выборочная совокупность – это совокупность отобранных единиц. Все ее обобщающие показатели получили название выборочных. Между характеристиками выборочной совокупности и параметрами генеральной совокупности существует некоторое расхождение, которое называют ошибкой. Общая величина возможной ошибки выборочной совокупности слагается из: ошибки регистрации (несовершенство измерительных приборов, недостаточная квалификация наблюдателя, неточность подчетов и т.д.) и ошибки репрезентативности представляют собой расхождение между величиной полученных по выборке показателей и величиной этих показателей, которые были получены при проведенном с одинаковой степенью точности сплошным наблюдением. Для каждого конкретного выборочного наблюдения величина ошибки может быть определена по соответствующим формулам. В статистике приняты следующие условные обозначения: N – объем генеральной совокупности (число входящих в нее единиц); п – объем выборочной совокупности (число обследованных единиц); – генеральная средняя (среднее значение признака в генеральной совокупности); – выборочная средняя; р – генеральная доля (доля единиц, обладающих данным значением признака, в общем числе единиц генеральной совокупности); w – выборочная доля; – генеральная дисперсия; S2 – выборочная дисперсия; – среднее квадратическое отклонение признака в генеральной совокупности; S – среднее квадратическое отклонение признака в выборочной совокупности. Основные этапы проведения выборочного наблюдения определение нужного объема выборки и способа отбора; проведение отбора; обобщение данных и расчет выборочных характеристик; расчет ошибок выборки; распространение выборочных характеристик на генеральную совокупность. 7.2 Виды выборки, способы отбора и ошибки выборочного наблюдения По способу отбора (способу формирования) выборки единиц из генеральной совокупности распространены следующие виды выборочного наблюдения: простая случайная выборка (собственно-случайная); типическая (стратифицированная); серийная (гнездовая); механическая; комбинированная; ступенчатая. Простая случайная выборка (собственно-случайная) есть отбор единиц из генеральной совокупности путем случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности. Отбор проводится методом жеребьевки или по таблице случайных чисел. Типическая (стратифицированная) выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц. Для серийной (гнездовой) выборки характерно то, что генеральная совокупность первоначально разбивается на определенные равновеликие или неравновеликие серии (единицы внутри серий связаны по определенному признаку), из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение. Механическая выборка представляет собой отбор единиц через равные промежутки (по алфавиту, через временные промежутки, по пространственному способу и т.д.). При проведении механического отбора генеральная совокупность разбивается на равные по численности группы, из которых затем отбирается по одной единице. Комбинированная выборка основана на сочетании нескольких способов выборки. Многоступенчатая выборка есть образование внутри генеральной совокупности вначале крупных групп единиц, из которых образуются группы, меньшие по объему, и так до тех пор, пока не будут отобраны те группы или отдельные единицы, которые необходимо исследовать. Выборочный отбор может быть: повторным (вероятность выбора любой единицы не ограничена). Данный вид выборки очень редко можно встретить в социально-экономической жизни; бесповторным (выбранная единица в исходную совокупность не возвращается). Основной задачей при выборочном исследовании является определение ошибок выборки. Принято различать среднюю и предельную ошибки выборки. Расчет предельной ошибкиповторной случайной выборки: - предельная ошибка для средней  - предельная ошибка для доли 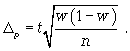 где t – нормированное отклонение – «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки и определяется по таблице значений интегральной функции Лапласа при заданной вероятности. Расчет предельной ошибки бесповторной случайной выборки: - предельная ошибка для средней 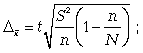 - предельная ошибка для доли 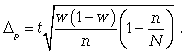 Для типической выборки величина стандартной ошибки зависит от точности определения групповых средних. Так, в формуле предельной ошибки типической выборки учитывается средняя из групповых дисперсий, т.е.  При серийной выборке величина ошибки выборки зависит не от числа исследуемых единиц, а от числа обследованных серий (s) и от величины межгрупповой дисперсии: 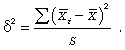 Серийная выборка, как правило, проводится как бесповторная, и формула ошибки выборки в этом случае имеет вид:  где – межсерийная дисперсия; s – число отобранных серий; S – число серий в генеральной совокупности. Все вышеприведенные формулы применимы для большой выборки. Кроме большой выборки используются так называемые малые выборки (n < 30), которые могут иметь место в случаях нецелесообразности использования больших выборок. Теория малых выборок была разработана английским статистиком Стьюдентом в начале 20 века. В 1908 г. он выявил специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При n больше 100 дают такие же результаты, что и таблицы интеграла вероятностей Лапласа, при 30< n < 100 различия получаются незначительные. Поэтому на практике к малым выборкам относятся выборки объемом менее 30 единиц. При расчете ошибок малой выборки необходимо учесть два момента: 1) формула средней ошибки имеет вид  2) при определении доверительных интервалов исследуемого показателя в генеральной совокупности или при нахождении вероятности допуска той или иной ошибки необходимо использовать таблицы вероятности Стьюдента, где Р = S (t, n), при этом Р определяется в зависимости от объема выборки и t. В статистических исследованиях с помощью формулы предельной ошибки можно решать ряд задач. 1. Определять возможные пределы нахождения характеристики генеральной совокупности на основе данных выборки. Доверительные интервалы для генеральной средней можно установить на основе соотношений где – генеральная и выборочная средние соответственно; – предельная ошибка выборочной средней. Доверительные интервалы для генеральной доли устанавливаются на основе соотношений 2. Определять доверительную вероятность, которая означает, что характеристика генеральной совокупности отличается от выборочной на заданную величину. Доверительная вероятность является функцией от t, где Доверительная вероятность по величине t определяется по специальной таблице. 3. Определять необходимый объем выборки с помощью допустимой величины ошибки: Чтобы рассчитать численность п повторной и бесповторной простой случайной выборки, можно использовать следующие формулы: 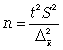 (для средней при повторном способе); (для средней при повторном способе);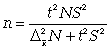 (для средней при бесповторном способе); (для средней при бесповторном способе);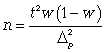 (для доли при повторном способе); (для доли при повторном способе);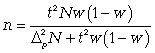 (для доли при бесповторном способе). (для доли при бесповторном способе). |
