Роль статистики в бизнесе. Лекция+1+ВВЕДЕНИЕ+РОЛЬ+СТАТИСТИКИ+В+БИЗНЕСЕ. Тема 1 введение роль статистики в бизнесе 1 Статистические методы в управлении Статистика
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
ТЕМА 9 МОДЕЛИРОВАНИЕ СЕЗОННЫХ КОЛЕБАНИЙ Уровни временного ряда являются суммой двух составляющих: систематической (детерминированной, регулярной); случайной (нерегулярной, непредсказуемой), не зависящей от времени Регулярная составляющая, в общем случае, может складываться из тренда, циклической компоненты и сезонной компоненты. Однако, регулярная составляющая не обязательно должна включать все три компоненты. Случайная (нерегулярная) компонента. Экономисты разделяют факторы, под действием которых формируется нерегулярная компонента, на 2 вида: Факторы резкого, внезапного действия (например, стихийные бедствия, эпидемии и др.), как правило, вызывает более значительные отклонения по сравнению со случайными колебаниями – иногда такие отклонения называют катастрофическими колебаниями. Текущие факторы вызывают случайные колебания, являющиеся результатом действия большого числа побочных причин. Влияние каждого из текущих факторов незначительно, но ощущается их суммарное воздействие. Цель сезонной декомпозиции и корректировки временного ряда состоит в том, чтобы разложить ряд на составляющие: тренд, сезонную компоненту и нерегулярную составляющую. В общем случае временной ряд можно представить из четырех различных компонент: Сезонной компоненты (обозначается St, где t обозначает момент времени) Тренда (Tt) Циклической компоненты (Ct) Случайной, нерегулярной компоненты (Et) Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который, к тому же, меняется от цикла к циклу. Тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (TtCt) (для простоты обозначений далее TtCt—>Tt). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако можно выделить два основных способа, с помощью которых они могут взаимодействовать – аддитивно и мультипликативно. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов. Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели следующий
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент. Общий вид мультипликативной модели выглядит так:
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (E) и случайной (E) компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты. Построение аддитивной и мультипликативной моделей сводится к расчету значений T , S и E для каждого уровня ряда. Процесс построения модели включает в себя следующие шаги. Выравнивание исходного ряда методом скользящей средней. Расчет значений сезонной компоненты S Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (T+E) в аддитивной или (T·E) в мультипликативной модели. Аналитическое выравнивание уровней (T+E) или (T·E) и расчет значений T с использованием полученного уравнения тренда. Расчет полученных по модели значений (T+E) или (T·E). Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок E для анализа взаимосвязи исходного ряда и других временных рядов. ТЕМА 10 СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СВЯЗЕЙ МЕЖДУ ЯВЛЕНИЯМИ И ИХ ИСПОЛЬЗОВАНИЕ ДЛЯ УПРАВЛЕНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИМИ ПРОЦЕССАМИ Современная наука об обществе объясняет суть явлений через изучение взаимосвязей явлений. Объем продукции предприятия связан с численностью работников, стоимостью основных фондов и т. д. Различают два типа взаимосвязей между различными явлениями и их признаками: функциональную или жестко детерминированную и статистическую или стохастически детерминированную. Функциональная связь – это вид причинной зависимости, при которой определенному значению факторного признака соответствует одно или несколько точно заданных значений результативного признака. Стохастическая связь – это вид причинной зависимости, проявляющейся не в каждом отдельном случае, а, в общем, в среднем, при большом числе наблюдений. Например, изучается зависимость роста детей от роста родителей. В семьях, где родители более высокого роста, дети в среднем ниже, чем родители. И, наоборот, в семьях, где родители ниже ростом, дети в среднем выше, чем родители. Еще один пример: потребление продуктов питания пенсионеров зависит от душевого дохода: чем выше доход, тем больше потребление. Однако такого рода зависимости проявляются лишь при большом числе наблюдений. Корреляционная связь – это неполная вероятностная зависимость между результативным и факторным признаками, которая проявляется только в массе наблюдений; каждому отдельному значению факторного признака Xможет соответствовать множество различных значений результативного (У). Задачами корреляционного анализа являются: изучение степени тесноты связи 2-х и более явлений; отбор факторов, оказывающих наиболее существенное влияние на результативный признак; 3) выявление неизвестных причинных связей. Исследование корреляционных зависимостей включает ряд этапов: постановка цели исследования; сбор информации; спецификация модели - построение регрессионной модели, т. е. нахождение аналитического выражения связи; расчет параметров модели оценку адекватности модели, ее экономическую интерпретацию и практическое использование. Корреляционная связь между признаками может возникать различными путями. Важнейший путь – причинная зависимость результативного признака (его вариации) от вариации факторного признака. Например, X– балл оценки плодородия почв, У – урожайность сельскохозяйственной культуры. Здесь ясно, какой признак выступает как независимая переменная (фактор), а какой как зависимая переменная (результат). Очень важно понимать суть изучаемой связи, поскольку корреляционная связь может возникнуть между двумя следствиями общей причины. Здесь можно привести множество примеров. Так, классическим является пример, приведенный известным статистиком начала XX в. А.А.Чупровым. Если в качестве признака Xвзять число пожарных команд в городе, а за признак У - сумму убытков в городе от пожаров, то между признаками X и У в городах обнаружится значительная прямая корреляция. В среднем, чем больше пожарников в городе, тем больше убытков от пожаров. В чем же дело? Данную корреляцию нельзя интерпретировать как связь причины и следствия, оба признака – следствия общей причины – размера города. В крупных городах больше пожарных частей, но больше и пожаров, и убытков от них за год, чем в мелких. Современный пример. Сразу после 17 августа 1998 г. резко возросли цена валюты и объем покупки валюты частными лицами. Здесь также нельзя рассматривать эти два явления как причину и следствие. Общая причина – обострение финансового кризиса, приведшее к росту курсовой стоимости валюты и стремлению населения сохранить свои накопления в твердой валюте. Такого рода корреляцию называют ложной корреляцией. Корреляция возникает и в случае, когда каждый из признаков и причина, и следствие. Например, при сдельной оплате труда существует корреляция между производительностью труда и заработком. С одной стороны, чем выше производительность труда, тем выше заработок. С другой – высокий заработок сам по себе является стимулирующим фактором, заставляющим работника трудиться более интенсивно. По направлению выделяют связь прямую и обратную, по аналитическому выражению – прямолинейную и нелинейную. В начальной стадии анализа статистических данных не всегда требуются количественные оценки, достаточно лишь определить направление и характер связи, выявить форму воздействия одних факторов на другие. 10.1 Парная регрессия и корреляция Парная регрессия представляет собой регрессию между двумя переменными – 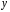 и и 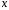 , т. е. модель вида: , т. е. модель вида: , ,где 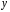 – зависимая переменная (результативный признак); – зависимая переменная (результативный признак); 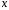 – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными 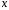 и и 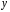 нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина 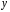 складывается из двух слагаемых: складывается из двух слагаемых: , ,где 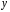 – фактическое значение результативного признака; – фактическое значение результативного признака; 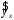 – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; – теоретическое значение результативного признака, найденное исходя из уравнения регрессии;  – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.Случайная величина  называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных. называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака 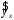 , подходят к фактическим данным , подходят к фактическим данным 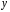 . .К ошибкам спецификации относятся неправильный выбор той или иной математической функции для 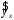 и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.Наряду с ошибками спецификации могут иметь место ошибки выборки, которые имеют место в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии. Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем, статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например, в результате наличия скрытых доходов. Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. В парной регрессии выбор вида математической функции  может быть осуществлен тремя методами: может быть осуществлен тремя методами:графическим; аналитическим, т.е. исходя из теории изучаемой взаимосвязи; экспериментальным. При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рисунке 1: 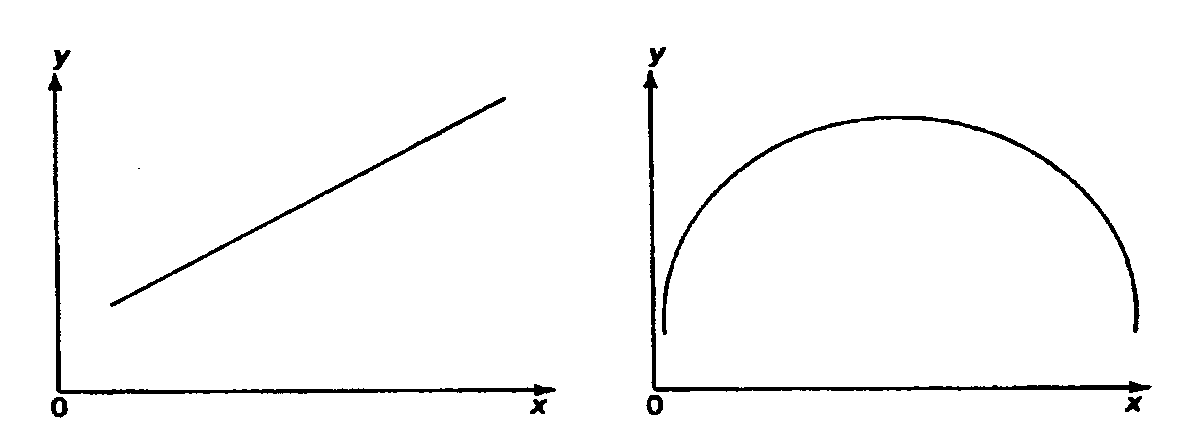 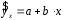 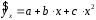 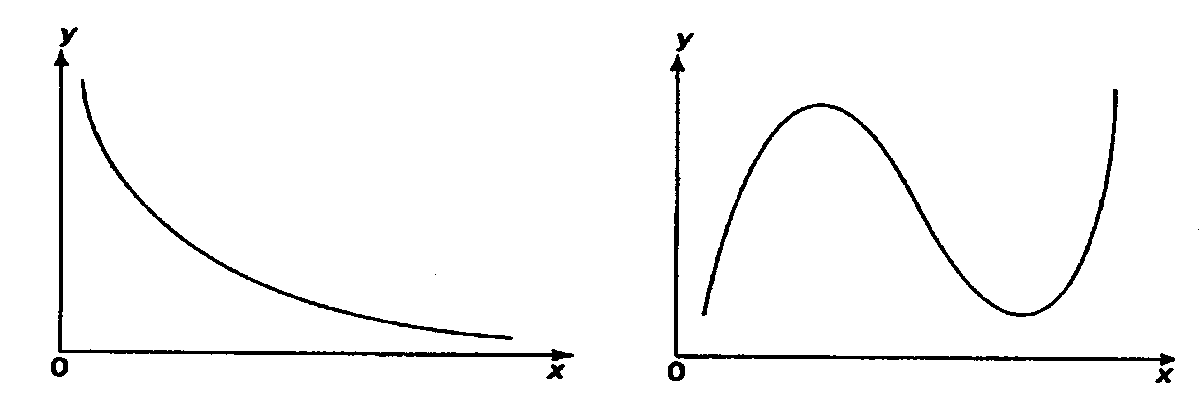 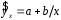 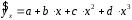  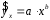 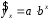 Рисунок 1 – Основные типы кривых, используемые при количественной оценке связей между двумя переменными Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков. При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии  , рассчитанной при разных моделях. , рассчитанной при разных моделях.Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии 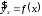 , то фактические значения результативного признака совпадают с теоретическими , то фактические значения результативного признака совпадают с теоретическими  , т.е. они полностью обусловлены влиянием фактора , т.е. они полностью обусловлены влиянием фактора 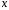 . В этом случае остаточная дисперсия . В этом случае остаточная дисперсия 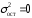 . .В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии, факторов. Иными словами, имеют место отклонения фактических данных от теоретических 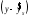 . Величина этих отклонений и лежит в основе расчета остаточной дисперсии: . Величина этих отклонений и лежит в основе расчета остаточной дисперсии: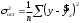 . .Чем меньше величина остаточной дисперсии, тем меньше влияние не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным. Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной 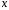 . Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при . Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при 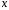 должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени  , то требуется объем информации уже не менее 14 наблюдений. , то требуется объем информации уже не менее 14 наблюдений. |
