Роль статистики в бизнесе. Лекция+1+ВВЕДЕНИЕ+РОЛЬ+СТАТИСТИКИ+В+БИЗНЕСЕ. Тема 1 введение роль статистики в бизнесе 1 Статистические методы в управлении Статистика
 Скачать 0.92 Mb.
|
ТЕМА 12 ВЫБОР АЛЬТЕРНАТИВ12.1 Метод анализа иерархии12.1.1 Общее описаниеЦель метода анализа иерархий обоснование выбора наилучшей из предлагаемых альтернатив, характеристики которых являются векторами с разнородными, в том числе и с нечетко определенными, отдельными компонентами. Суть метода анализа иерархий заключается в поэтапном решении следующих взаимосвязанных частных задач: построение иерархической структуры показателей (признаков); оценивание значимости отдельных частных показателей для каждого уровня иерархии; сравнение имеющихся альтернатив и выбор наилучшей из них. В результате должна быть выражена относительная степень (интенсивность) взаимодействия элементов в иерархии. Метод анализа иерархии включает процедуры синтеза множественных суждений, базирующихся на результатах парных сравнений, которые затем выражаются численно, оценки приоритетности (важности) критериев (отдельных показателей), а также оценки альтернативных решений и нахождения наилучшего из них. Полученные результирующие значения являются оценками в шкале отношений, что соответствует жестким оценкам. Исходным материалом, на основании которого ЛПР может получить достаточное, четкое и ясное представление о превосходстве одного элемента над другим, являются интуиция и субъективные оценки, несмотря на то, что суждения и их интенсивность характеризуют выражение внутренних чувств и склонностей конкретных экспертов.. Суждения расширяют рамки общения, укрупняя элементы, имеющиеся на определенном уровне иерархии. Изложенное дает представление об основных принципах метода анализа иерархий. Подробнее эти принципы будут изложены в дальнейшем, при детальном рассмотрении процедур. 12.1.2 Основные этапы метода анализа иерархийМетод анализа иерархий включает следующие основные этапы, значимость которых различна для разных задач и ситуаций. 1. Описание проблемы и определение цели исследований. 2. Построение иерархии, начиная с вершины (цели с точки зрения управления), через промежуточные уровни (критерии, от которых зависят последующие уровни), к самому нижнему уровню (который обычно является перечнем альтернатив). 3. Построение матриц влияния элементов верхнего (предыдущего) уровня на элементы нижнего (следующего) уровня (для каждого из нижних уровней) по одной матрице для каждого элемента, примыкающего сверху уровня. В полной простой иерархии любой элемент воздействует на каждый элемент примыкающего сверху уровня. Элементы каждого уровня сравниваются друг с другом относительно степени их воздействия на элемент предыдущего уровня и получают квадратную матрицу суждений. Реальные иерархические структуры весьма редко бывают полными простыми иерархиями и их, в ряде случаев, целесообразно декомпозировать на подуровни. Парные сравнения проводятся в терминах определения степеней доминирования (предпочтения) одного из элементов над другим, которые затем выражаются в целых числах (табл. 3.1 для величин суждений). Если элемент А доминирует над элементом Б, то клетка, соответствующая строке А и столбцу Б, заполняется целым числом, а клетка, соответствующая строке Б и столбцу А, заполняется обратным к нему числом (дробью). Если элемент Б доминирует над элементом А, то происходит обратное. Если считается, что элементы А и Б одинаковы, то в обе позиции ставится единица. 4. На этапе 3 для получения каждой матрицы требуется n(n1)/2 суждений (парных сравнений). Результатом этапа 3 (сравнения значимости влияния элементов следующего уровня на элементы предыдущего уровня) является набор квадратных матриц N1, N2, , Nk с элементами (aij,i, j = 1, 2,…, n), где k число элементов предыдущего уровня иерархии, n число элементов следующего уровня иерархии. Если иерархическая структура не является полной простой иерархией, то возможно уменьшение количества сравнений, т. е. упрощение процесса получения результатов парных сравнений. Таблица 1
5. После проведения всех парных сравнений для элементов соседних уровней (получения набора матриц) следует вычислить весовые коэффициенты дуг. Для каждой из матриц Ni определяется нормализованный вектор локальных приоритетов, со следующими компонентами:  (1)где n размерность матрицы; aji элемент j-ой строки матрицы. Таким образом, мат рице Ni сопоставляется вектор ai . Нормирование компонент осуществляется путем деления каждой компоненты вектора ai на сумму всех компонент этого вектора:  (2)Нормированный вектор bi соответствует весовым коэффициентам дуг, соединяющих i-й элемент предыдущего уровня со всеми элементами следующего уровня. Если ввести в рассмотрение матрицу влияний элементов нижнего уровня на элементы предыдущего уровня Bl, где l номер уровня иерархии, то векторы bi будут являться ее столбцами. 6. После получения данных (обработки матриц суждений Ni по формулам (1) и (2)) следует определить их согласованность. Степень согласованности для каждой матрицы приближенно вычисляется следующим способом: суммируется каждый столбец матрицы суждений, и сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца на вторую компоненту и т. д. Полученные числа суммируются и получается величина 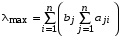 (3)Используя отклонение  от n, находят индекс согласованности (ИС), сравнивая который с соответствующими средними значениями для случайных элементов, получают отношение согласованности (ОС).Средние согласованности для случайных матриц различного порядка
7. Этапы 3, 4, 5 и 6 проводятся для всех уровней иерархии. 8. Производится поэтапная оценка весовых коэффициентов элементов каждого следующего уровня иерархии:  где Ci1 вектор весовых коэффициентов элементов предыдущего уровня, а Bi - матрица влияний элементов нижнего уровня на элементы предыдущего уровня, состоящая из векторов, полученных по формуле (2); i номер уровня иерархии. 9. Согласованность всей иерархии можно найти, перемножая каждый индекс согласованности на приоритет соответствующего критерия и суммируя полученные числа. Затем результат делится на выражение такого же типа, но со случайным индексом согласованности, соответствующим размерам каждой взвешенной приоритетами матрицы. Приемлемым является отношение согласованности около 10 % или менее. В противном случае качество суждений следует улучшить, изменив способ, следуя которому задаются вопросы при проведении парных сравнений. Если это не помогает улучшить согласованность, то, вероятно, задачу следует более точно структурировать, т. е. сгруппировать аналогичные элементы под более значащими критериями. Потребуется возврат к этапу 2, хотя пересмотра могут потребовать только сомнительные части иерархии. Замечания: 1. При проведении оценок следует иметь в виду все сравниваемые элементы. Для получения обоснованных численных сравнений не следует сравнивать более чем 7±2 элементов, так как в таком случае погрешность, обусловленная приближенностью метода, мало меняет результат для каждой относительной величины. Для неполной иерархии, разделяемой на частичные иерархии, это условие обычно выполняется. 2. Работы с более широким классом объектов следует осуществлять посредством иерархической декомпозиции. Элементы группируются (в качестве первой оценки) в сравниваемые классы приблизительно из семи элементов в каждом. Элемент с наивысшим весом в классе также включается в следующий класс элементов с большими весами и как своеобразный стержень между двумя классами придает однородность шкале. Процедура повторяется многократно, пока все элементы не будут взвешены. Сложная математика не может «улучшить» то, что ЛПР не хочет менять. | ||||||||||||||||||||||||||||||||||||||||||||||