Линейная алгебра. Тема Действительные числа
 Скачать 2.01 Mb.
|
|
Тема 8. Парабола Определение 9.16. Геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой, именуется параболой. у2 = 2 px — каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси OX. Исследуем форму параболы. 1. Найдем точки пересечения с осями. OX , OY : y = 0, х = 0, О(0; 0). Определение 9.17. Точка О называется вершиной параболы. 2. Из вида уравнения следует, что линия симметрична относительно оси OX . 3. x ∈ [0; + ∞). Следовательно, кривая расположена правее оси OY . Построим данную кривую (рис. 9.11). 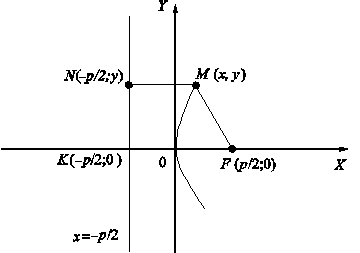 Рис. 9.11 Если парабола симметрична относительно OY и имеет вершину в начале координат, то ее каноническое уравнение имеет вид x2 = 2 py (рис. 9.12). 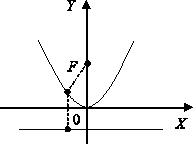 Рис. 9.12 Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 180–181. 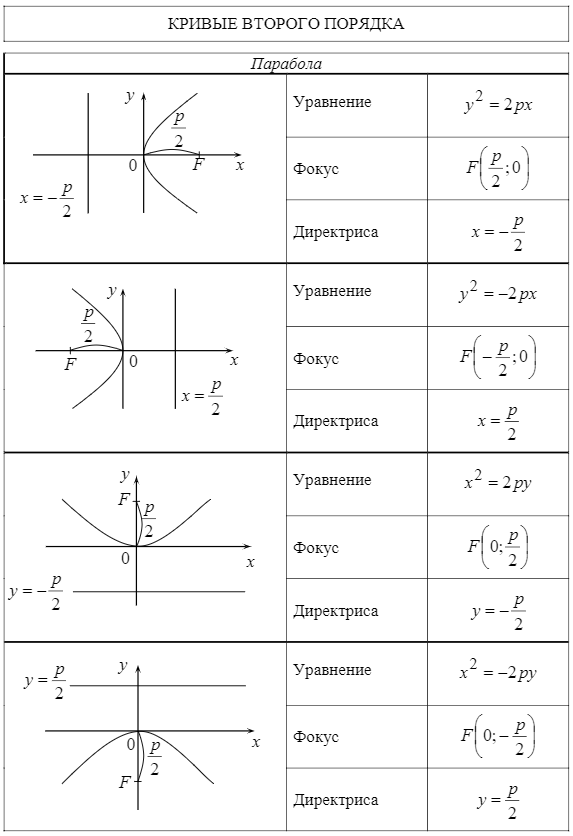 Цит. по: Высшая математика в схемах и таблицах / Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 25. 4.53. Парабола с вершиной в начале координат проходит через точку A (2; 4) и симметрична относительно оси Ox. Найти фокус и уравнения параболы и ее директрисы. Решение Так как парабола проходит через точку O (0; 0) и симметрична относительно оси Ox, то ее уравнение y2 = 2 px. Подставляя координаты точки А в это уравнение, т.е. 42 = 2p × 2, найдем параметр p = 4. Следовательно, уравнение параболы y2 = 8 x. Уравнение ее директрисы x = –2, фокус параболы F (2; 0) ( рис. 9.14 ) . 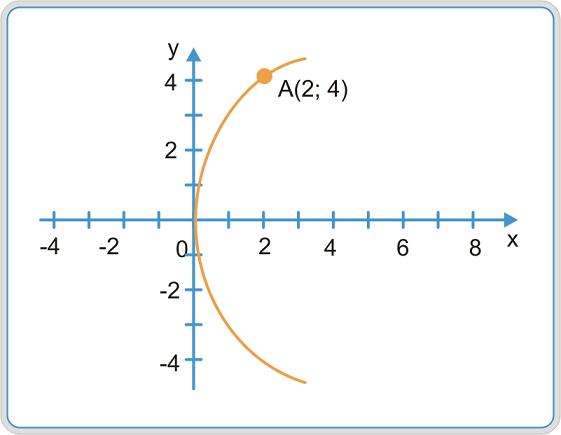 Рис. 9.14 4.54. Через точку А (3; –1) провести такую хорду параболы  которая делилась бы в данной точке пополам.Решение Для построения параболы представим ее в виде  т.е. вершина параболы (2; –3). Уравнение прямой (хорды), проходящей через точку А (3; –1) в соответствии с имеет вид: y + 1 = k ( x – 3). Точки пересечения хорды с параболой определяются системой: 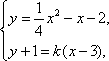 решение которой, после исключения y , сводится к уравнению:  или x 2 – 4( k + 1) x + 4(3 k – 1) = 0. (*)По условию точка А (3; –1) делит хорду пополам, следовательно,  где x1 и x2 — корни уравнения (*).По теореме Виета x1 + x2 = 4( k + 1), следовательно, 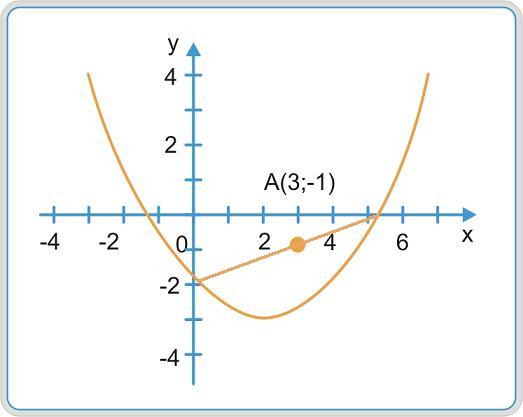 или xA = 2( k + 1) = 3, откуда  и уравнение хорды:  или x – 2 y – 5 = 0 (рис. 9.15). Рис. 9.15 |