Линейная алгебра. Тема Действительные числа
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
Тема 5. Свойства операций над матрицами В), если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.Теорема 8.16.Любую невырожденную квадратную матрицу с помощью элементарных преобразований можно привести к единичной матрице того же порядка. Применяя ту же последовательность элементарных преобразований к единичной матрице, можно получить обратную матрицу к данной. Обычно элементарные преобразования производят над данной матрицей и единичной одновременно. Для этого составляют расширенную матрицу, в левой части которой стоит исходная матрица, а в правой -единичная матрица того же порядка. С помощью элементарных преобразований в левой части создают единичную матрицу, параллельно в правой части автоматически создается обратная матрица. Пример 8.17. Пусть дана матрица Составим расширенную матрицу:  Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. -2-е изд., стер. -М.: КНОРУС, 2008. -С. 134–137.
Цит. по: Высшая математика в схемах и таблицах / Н.С. Знаенко. -Ульяновск: ООО «Вектор-С», 2008. -С. 9. Пример. Для матрицы  найти обратную матрицу найти обратную матрицу Решение:  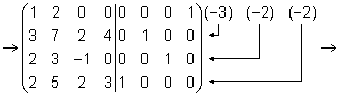 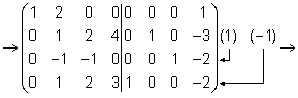    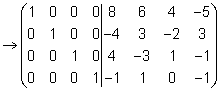 . .Итак, 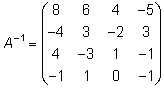 . .Мы проверили ранее, что | A | ≠ 0, следовательно, A имеет обратную матрицу. Запишем рядом с матрицей A матрицу E размерности 4 × 4 и приведем (A / E) к ступенчатому виду Гаусса. Легко сделать проверку умножением матриц A × A –1 = A –1 × A = E . Цит. по: Математика [Электронный ресурс]: учебный курс / Г.А. Питерцева. -Электронный курс. -М: МИЭМП, 2007. - Режим доступа к курсу: http://e-college.ru. - П. 6.7. Приведем основные свойства операций над матрицами.  Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. -2-е изд., стер. -М.: КНОРУС, 2008. -С. 129–130. Тема 6. Системы линейных уравнений
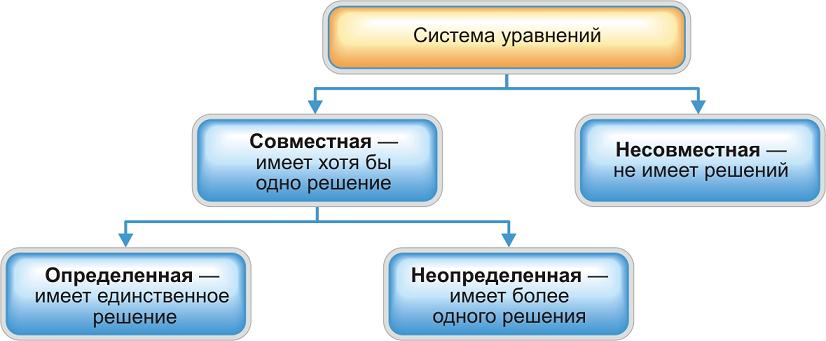
Цит. по: Высшая математика в схемах и таблицах / Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 13. Системы линейных уравнений Определение 8.40. Система вида  называется системой m линейных уравнений с n неизвестными, где x1, x2, …, xn — неизвестные, aij , i = Определение 8.41. Если все свободные члены равны нулю, то система называется однородной, и неоднородной — в противном случае. Определение 8.42. Решением системы называется совокупность из n чисел с1, с2, …, сn, при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств. Определение 8.43. Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае. Определение 8.44. Совместная система называется определенной, если она имеет единственное решение, и неопределенной — в противном случае. При изучении систем исследуют три вопроса: 1) совместна система или нет; 2) если система совместна, то является ли она определенной или неопределенной; 3) нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной. Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 142. Тема 7. Матрица системы Система m линейных уравнений с n переменными имеет вид 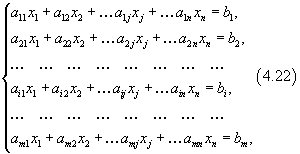 или в краткой записи с помощью знаков суммирования: В матричной форме система (4.22) имеет вид AX = B, (4.24) где  называются соответственно матрицей системы, матрицами-столбцами переменных и свободных членов. В векторной форме система (4.22) имеет вид где 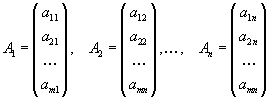 - векторы-столбцы при переменных x1 , х2, ..., хn; В - вектор-столбец свободных членов. - векторы-столбцы при переменных x1 , х2, ..., хn; В - вектор-столбец свободных членов.Если число уравнений равно числу переменных, т.е. m = n, и квадратная матрица А - невырожденная (|A | ≠ 0), то система (4.22) имеет единственное решение: X = A –1B. (4.26) Рассмотрим систему 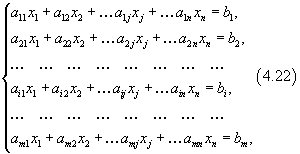 в общем виде, когда число уравнений m не равно числу переменных, т.е. m ≠ n. Расширенной матрицей системы называется матрица (A \ В), полученная из матрицы системы А добавлением к ней столбца свободных членов этой системы, т.е. 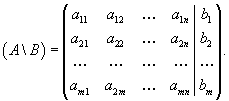 Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы ( A \ В) этой системы. Результаты исследования системы (4.22) приведены в виде схемы (рис. 4.3). 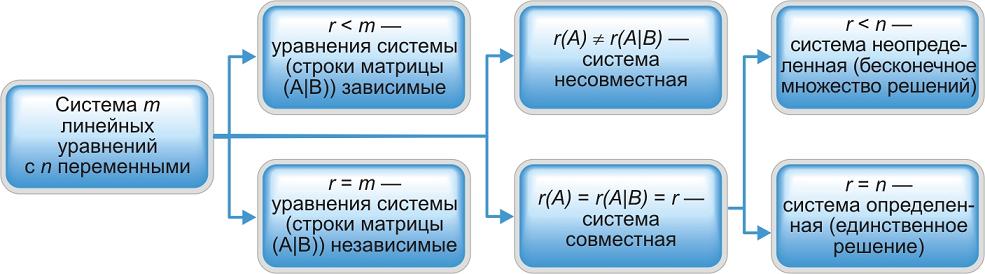 Рис. 4.3 Пусть r < n; r переменных x1 , х2 , …, xr , называются основными (или базисными), если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные n - r переменных называются неосновными (или свободными). Решение системы (4.22), в котором все n - r неосновных переменных равны нулю, называется базисным. Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным. Совместная система m линейных уравнений с n переменными (m < n) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее числа сочетаний Цит. по: Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. - М.: Высшее образование, 2009. - (Основы наук) - С. 110, 112–113. Решение произвольных систем линейных неоднородных уравнений Пусть дана неоднородная система m линейных уравнений с n неизвестными  Предположим, что система совместна, т. е. r (A ) =  Первые r уравнений системы линейно независимы. Остальные выражаются через них. Следовательно, их можно отбросить.  Определение 8.45. Переменные, коэффициенты при которых образуют минор, отличный от нуля (базисный минор), называются базисными переменными (x1 , x2 , …, xr ). Остальные переменные xr + 1 , …, xn называются свободными. Дадим свободным переменным произвольные числовые значения xr+ 1 = сr+ 1 , xr+ 2 = с r+ 2 , …, xn = cn . Запишем систему в виде  Мы получили систему из r линейных уравнений с r неизвестными, определитель которой отличен от нуля. Она имеет единственное решение.  - общее решение. - общее решение.Определение 8.46. Выражение базисных переменных через свободные называется общим решением системы. Определение 8.47. Решение системы, полученное из общего при конкретных значениях свободных переменных, называется частным решением. Частных решений у системы бесконечно много, все они содержатся в общем решении. Определение 8.48. Частное решение, полученное из общего, когда свободные переменные равны нулю, называется базисным решением системы. Определение 8.49. Базисное решение, координаты которого неотрицательны, называется опорным решением системы. Пример 8.21.  Переменные х1 и х2 - базисные, х3 и х4 - свободные. 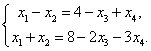 Сложим уравнения и результат разделим на 2. Вычтем из второго уравнения первое и результат разделим на 2. Получим 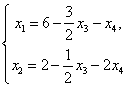 - общее решение. Из него можно получить частные и базисное решения.  - частное решение, полученное при х3 = 2 и х4 = 1. 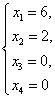 - базисное решение при х3 = х4 = 0. Оно же является опорным. Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 147–149. |

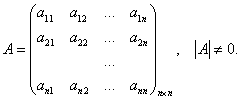
 -матрица, присоединенная к матрице А ;
-матрица, присоединенная к матрице А ;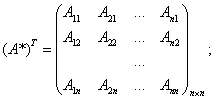



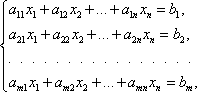
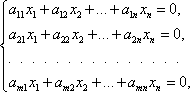 — однородная система
— однородная система