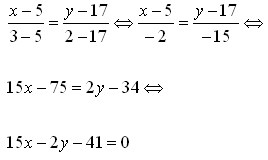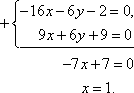Линейная алгебра. Тема Действительные числа
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
|
Тема 8. Метод Гаусса 4. Методом Гаусса можно решить любую систему уравнений вида (4.22 - см. Тема 7). Для этого составляют расширенную матрицу коэффициентов (АВ), приписывая к матрице А столбец свободных членов В , затем матрицу (АВ) с помощью элементарных преобразований приводят к ступенчатому виду (так называемый «прямой ход»); далее по полученной матрице выписывают новую систему и решают ее методом исключения переменных: начиная с последних (по номеру) переменных находят все остальные (так называемый «обратный ход»). Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 35. Определение 8.50. Элементарными преобразованиями системы называются: 1) умножение уравнения на число, отличное от нуля; 2) прибавление к одному уравнению другого уравнения, умноженного на некоторое число, отличное от нуля. 3) перестановка двух уравнений; 4) отбрасывание уравнения 0 = 0. Если получено уравнение 0 = k , то система несовместна. Цит. по: Математика для экономистов: учебное пособие / С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 149–150. 2.3. Методом Гаусса решить систему: 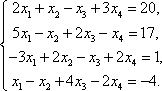 Решение. Выпишем расширенную матрицу системы. Необходимо на первом шаге, чтобы а11 ≠ 0, но удобнее для вычислений, чтобы а11 = 1. Поэтому поменяем местами первую и четвертую строки, чтобы а11 стал равным 1: 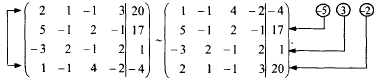 Шаг 1. Умножим элементы первой строки на – 5, 3 и – 2 и прибавим их соответственно к элементам второй, третьей и четвертой строк, чтобы под элементом а 11 в первом столбце образовалась «ступенька» из нулей. Для проведения второго шага необходимо, чтобы в новой матрице а22 ≠ 0 , но удобнее, чтобы а22 = 1 или а22 = –1. Поэтому переставим вторую и третью строки: 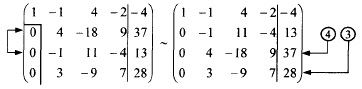 Шаг 2. Элементы второй строки умножаем на 4 и 3 и прибавляем соответственно к элементам третьей и четвертой строк, тогда под элементом a22 во втором столбце появится вторая «ступенька». Шаг 3. Так как в полученной матрице а33 = 26 ≠ 0 , умножаем элементы третьей строки на 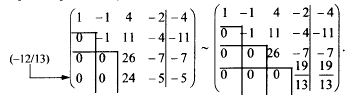 Расширенная матрица приведена к ступенчатому виду. Соответствующая ей система имеет вид: 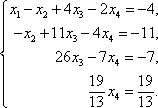 Из последнего уравнения х4 = 1, из третьего из второго х2 = 11 + 11х3 – 4х 4 = 11 + 110 – 41 = 7, из первого х1= –4 + х2 – 4х3 + 2х4 = –4 + 7 – 4 × 0 + 2 × 1 = 5. Ответ: (5; 7; 0; 1) . Замечание. Обратный ход метода Гаусса можно проводить и с расширенной матрицей, не переходя к системе, если эту матрицу с помощью элементарных преобразований привести к диагональной. Умножим элементы четвертой строки на 13/19. Затем элементы последней строки (а44 =1 ≠ 0) умножим на 7, 4, 2 и прибавим соответственно к элементам третьей, второй и первой строк: 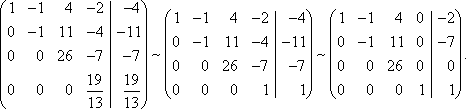 Далее умножим элементы третьей строки на 1/26, а затем, учитывая, что а33= 1 ≠ 0, — на (–4) и (–11) и прибавим к элементам первой и второй строк, а потом от первой строки отнимаем вторую (а22= – 1 ≠ 0): 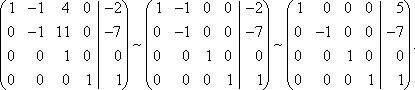 Левая часть расширенной матрицы приведена к диагональному виду. Выпишем систему:  Ответ: (5; 7; 0; 1) . 2.4. Методом Гаусса решить систему: 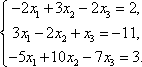 Решение. Выпишем и преобразуем расширенную матрицу системы. Сначала прибавим к элементам первой строки элементы второй: 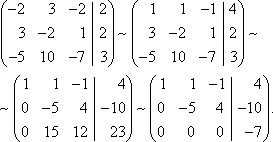 Последняя строка соответствует уравнению 0 × x1 + 0 × х2 + 0 × x3 = –7, которое не имеет решений; следовательно, система несовместна. Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 36–39. Пример. Найти общее решение системы:  Решение. Составим расширенную матрицу системы и приведем ее к ступенчатому виду Гаусса: 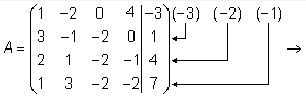 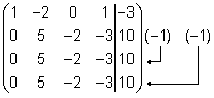  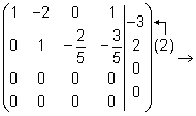 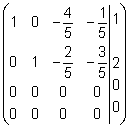 . .Первые две строки последней матрицы составляют расширенную матрицу системы, которая равносильна исходной. Выпишем систему линейных уравнений, соответствующую полученной расширенной матрице:  Неизвестные x1 и x2 , соответствующие опорным элементам строк полученной матрицы, называются базисными, каждое из них входит в новую систему с коэффициентом единица и только в одно уравнение. Остальные неизвестные называются свободными . Выразим базисные неизвестные через свободные: 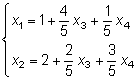 Свободные неизвестные — это произвольные числа, которые можно обозначить: x3 = с1 ; x4 = c2 , тогда x1 и x2 однозначно вычисляются и общее решение системы имеет вид:  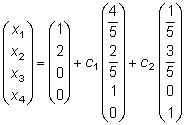 Число констант равно разности между числом неизвестных 4 и рангом матрицы системы 2. Цит. по: Математика [Электронный ресурс]: учебный курс / Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — Режим доступа к курсу: http://e-college.ru. — П. 6.10. Тема 9. Матричная форма решения системы Матричная форма решения системы 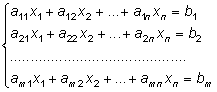 Обозначим через X столбец неизвестных, а через B столбец свободных членов. A — матрица системы:  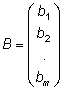  . .Тогда система может быть записана в виде: A × X = B (4). Это матричный вид системы . Рассмотрим случай, когда число уравнений равно числу неизвестных. Тогда матрица системы A является квадратной. Если определитель A отличен от нуля, то r ( A ) = n. Так как r ( A / B ) = n, следовательно, r ( A / B) = r (A) = n и по теореме Кронекера-Капелли система имеет решение. Это решение может быть записано формулой: X = A –1 × B, A –1 существует, так как | A | ≠ 0. Пример. Решить систему уравнений: 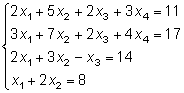 Решение. Составим матрицу этой системы:  Ранее мы нашли обратную матрицу для A : 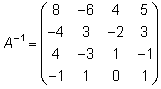 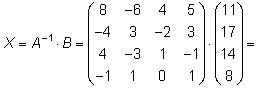 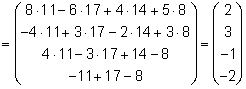 Ответ: x1 = 2; x2 = 3; x3 = –1; x4 = –2 . Рассмотрим применение систем линейных уравнений в экономике. Пример. Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент (свой для каждого банка). В начале года 3/8 вклада, который составляет 800 тыс. руб., вложили в первый банк, 1/8 во второй банк и оставшуюся часть вклада в третий банк. К концу года сумма этих вкладов стала равна 907 тыс. руб. Если бы первоначально 1/8 вклада положили в первый банк, 4/8 вклада — во второй банк, оставшуюся часть вклада — в третий банк, то к концу года сумма этих вкладов стала бы равна 894 тыс. руб. Если бы 4/8 вклада вложили в первый банк, 3/8 вклада — во второй банк, оставшуюся часть вклада — в третий банк, то к концу года сумма этих вкладов была бы равна 903 тыс. руб. Какой процент начисляет каждый банк? Решение. Введем следующие неизвестные: x1 — процент, начисляемый вкладчику в первом банке; x2 — процент, начисляемый вкладчику во втором банке; x3 — процент, начисляемый вкладчику в третьем банке. Вклад в первый банк составил (3/8) × 800 = 300 тыс. руб. Вклад во второй банк составил (1/8) × 800 = 100 тыс. руб. Вклад в третий банк составил (4/8) × 800 = 400 тыс. руб. Начислено в первом банке за год Начислено во втором банке за Начислено в третьем банке за Всего на вклад в 800 тыс. руб., сделанный в три банка (в первый было начислено 300 тыс. руб., во второй — 100 тыс. руб., в третий — 400 тыс. руб.), было начислено за год: 907 — 800 = 107 тыс. руб. Таким образом, первое уравнение системы: 3x1 + x2 + 4x3 = 107 Аналогично получим два других уравнения системы: x1 + 4x2 + 3x3 = 894 – 800 = 94 4x1 + 3x2 + x3 = 903 – 800 = 103. Получим систему трех линейных уравнений с тремя неизвестными: 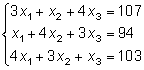 Решим эту систему методом Гаусса. 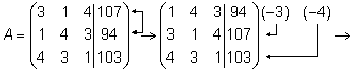 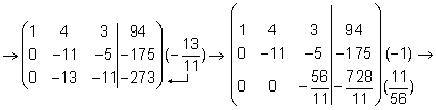  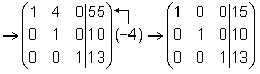 Система решена, она имеет единственное решение: x1 = 15; x2 = 10; x3 = 13. Таким образом, решив систему уравнений, мы нашли, что первый банк выплачивает 15% годовых, второй банк — 10% годовых, а третий банк — 13%. Цит. по: Математика [Электронный ресурс]: учебный курс / Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — Режим доступа к курсу: http://e-college.ru. — П. 6.11. 2.1. Методом обратной матрицы решить систему уравнений: 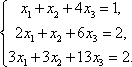 Решение. Обозначим:  Тогда в матричной форме система имеет вид: АХ = В. Определитель матрицы  т.е. обратная матрица А –1 существует : т.е. обратная матрица А –1 существует :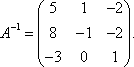 Теперь по формуле X = A-1 B:  Ответ :(3; 2; – 1). Цит. по: Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. — 2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. — (Серия «Золотой фонд российских учебников») — С. 35. Точнее данная теорема является частным случаем теоремы Лапласа. Аналитическая геометрия Тема 1. Прямая на плоскости Пример 1 Найдите уравнение прямой, проходящей через точку пересечения прямых 3x – 2y = 0 и 5x + y = 0 и точку M1 (5; 17). План решения 1. Найти точку пересечения прямых, которую обозначим M2, для этого требуется решить систему уравнений 2. Использовать уравнение прямой, проходящей через две точки M1 (x1 ; y1) и M2 (x2 ; y2): 3. Привести полученное уравнение к общему виду Ax + By + C = 0, воспользовавшись свойством пропорции (
Пример 3 Найдите координаты точки пересечения прямых 4x + 5y – 9 = 0 и –3x + 2y + 1 = 0. План решения 1. Решить систему уравнений Решение Решим систему уравнений методом алгебраического сложения (можно методом подстановки).  Подставим y = 1 в первое (второе) уравнение системы. Получим 4x + 5 × 1 – 9 = 0, 4x – 4 = 0, x = 1. Точка пересечения имеет координаты (1; 1). Пример 5 Даны вершины ΔABC , A (1; 2), B (–3; 3), C (5; 0). Найдите уравнение высоты треугольника, опущенной из вершины A . План решения 1. Найти координаты вектора 2. Высота, опущенная из вершины A, это прямая, проходящая через точку A и перпендикулярно стороне BC. Поэтому воспользоваться уравнением прямой, проходящей через точку и перпендикулярно вектору: A (x – x0 ) + B (y – y0) = 0.  3. В это уравнение вместо x0, y0 подставить координаты точки A , вместо A и B подставить координаты вектора 4. Привести уравнение к виду Ax + By + C = 0. Решение Подставим координаты точки и вектора в уравнение прямой A (x – x0) + B (y – y0) = 0: 8(x – 1) – 3(y – 2) = 0, 8x – 8 – 3y + 6 = 0, 8x – 3y – 2 = 0. Пример 7 Найдите уравнение прямой, проходящей через точки M1 (–4; 3) и M2 (5; –2). План решения 1. Использовать уравнение прямой, проходящей через две точки M1 (x1 ; y1) и M2 (x2 ; y2): 2. В это уравнение вместо x1, y1 подставить координаты точки M1, а вместо x2, y2 подставить координаты точки M2 . 3. Пользуясь свойством пропорции, привести полученное уравнение к виду Ax + By + C = 0. Решение Подставим координаты этих точек в уравнение прямой: –5(x + 4) = 9(y – 3), –5x – 20 – 9y + 27 = 0, –5x – 9y + 7 = 0. Пример 9 Найдите угол между прямыми y = 5x + 7 и 3x + 2y – 1 = 0. План решения 1. Привести уравнения прямых к виду l 1 : k1x + b1 и l 2 : k2x + b2 и определить угловые коэффициенты прямых k1 и k2 . 2. Воспользоваться формулой для нахождения угла φ между прямыми l1 и l2: Решение l 1 : y = 5x + 7, k = 5. 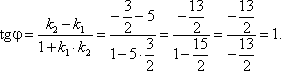 Следовательно, φ = 45°. Замечание Если tg φ < 0, то φ — тупой угол. Пример 11 Уравнение 4x – 3y + 24 = 0 преобразовать к уравнению «в отрезках». План решения Уравнение «в отрезках» имеет вид 1. Перенести свободный член вправо и разделить обе части уравнения на него. 2. Все коэффициенты и знаки убрать в знаменатели дробей. Решение 4x – 3y + 24 = 0, Пример 13 Определите уравнение прямой, отсекающей на оси Oy отрезок b = 3 и составляющей с осью Ox угол φ = 60°. План решения 1. Воспользоваться уравнением прямой с угловым коэффициентом: y = kx + b , где k = tg φ, φ — угол между прямой и осью Ox , b — отрезок, отсекаемый прямой на оси Oy . Решение y = kx + b , Пример 15 Стороны AB , BC , AC треугольника ABC заданы соответственно уравнениями 8x + 3y + 1 = 0, 2х + у - 1 = 0, 3x + 2y + 3 = 0. Определить координаты вершин треугольника.  План решения Вершины ΔABC — это точки пересечения соответствующих сторон. 1. Решить три системы уравнений, беря попарно уравнения сторон ΔABC . Решение
Пример 17 Даны вершины ΔABC , A (2; –2), B (3; –5), C (5; 7). Напишите уравнения его сторон. План решения  Каждая сторона треугольника — это прямая, проходящая через две точки. 1. Воспользоваться уравнением прямой, проходящей через две точки M1 (x1 ; y1) и M2 (x2 ; y2): 2. Определить через какие точки проходит каждая сторона. Решение Приведем уравнение к общему виду –3(x – 2) = 1(y + 2), –3x + 6 = y + 2. –3x – y + 4 = 0 или 3x + y – 4 = 0. 12(x – 3) = 2(y + 5), 12x – 36 = 2y + 10, 12x – 2y – 46 = 0 или 6x – y – 23 = 0. 9(x – 2) = 3(y + 2), 9x – 18 = 3y + 6, 9x – 3y – 24 = 0 или 3x – y – 8 = 0. В итоге уравнения сторон имеют вид: AB: 3x + y – 4 = 0, BC: 6x – y – 23 = 0, AC: 3x – y – 8 = 0. Цит. по: Методическое пособие-тренажер решения задач по высшей математике / Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 5–11. |