Линейная алгебра. Тема Действительные числа

• Название: Тема Действительные числа
• Дата: 21.09.2022
• Размер: 2.01 Mb.
• Имя файла: Линейная алгебра.docx
• Тип: Закон; #689818
• страница: 3 из 8

Тема 2. Метод решения систем линейных уравнений Крамера

Решение системы с помощью формул Крамера

Рассмотрим неоднородную систему n линейных уравнений с n неизвестными:



Теорема 8.22.(теорема Крамера). Если определитель матрицы, составленной из коэффициентов при неизвестных, отличен от нуля (|A| ≠ 0), то система имеет единственное решение, которое можно найти по формулам Крамера:



где D =|A| - главный определитель,

D_j - j -й вспомогательный определитель, который получен из определителя D заменой j -го столбца столбцом свободных членов.

Пример 8.20.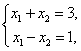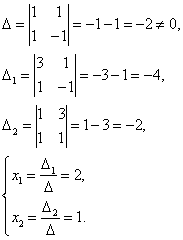 



Для системы двух линейных уравнений с двумя неизвестными справедливы свойства:

• 
  если главный определитель равен нулю и хотя бы один их вспомогательных определителей отличен от нуля, то система решений не имеет;
  
• 
  если главный определитель и оба вспомогательные определители равны нулю, то система имеет бесконечно много решений.
  

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 145–146.

Рассмотрим систему уравнений:

        (1)

Введем обозначения:



Если определитель системы Δ ≠ 0, то система (1) имеет единственное решение:  .

Пример: решить систему уравнений:



Решение:

Составим и вычислим определители:

.

Система имеет единственное решение:









Рассмотрим систему трех уравнений с тремя неизвестными.

            (2)

Введем обозначения: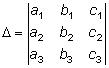

 - определитель системы.

Определители Δ_x, Δ_y, Δ_z получаются из определителя системы Δ путем замены соответственно первого, второго и третьего столбца столбцом свободных членов d₁, d₂, d₃.

Если определитель системы Δ ≠ 0, то существует единственное решение системы (2):



Пример. Решить систему уравнений: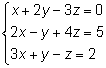



Вычисляем определитель системы Δ и определители Δ_x , Δ_y , Δ_z разложением определителей по элементам первой строки: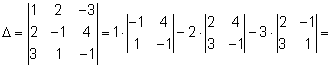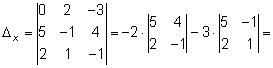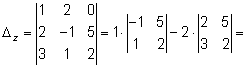

























Так как Δ ≠ 0, то система имеет только одно решение:

      

Рассмотрим применение систем в прикладных задачах.

Пример. Из двух сортов бензина образуются две смеси A и B. Смесь A содержит 60% бензина 1-го сорта и 40% 2-го сорта, смесь B содержит 80% бензина 1-го сорта и 20% 2-го сорта.

Сколько тонн смеси A и смеси B можно образовать, полностью, используя 50 тонн бензина 1-го сорта и 30 тонн бензина 2-го сорта?

Решение. Расположим все данные в таблице.

Наличие бензина		Вид смеси	Процентное содержание
1-го сорта	2-го сорта		1-го сорта	2-го сорта
50 т	30 т	А	60%	40%
		В	80%	20%

Обозначим через x₁ количество тонн смеси A, через x₂ количество тонн смеси B, которые можно образовать из наличного бензина, полностью его используя. На каждую тонну смеси A идет 0,6 т (60%) бензина 1-го сорта, на x₁ тонн - 0,6 x₁ тонн бензина 1-го сорта. Аналогично, на x₂ тонн смеси B уходит 0,8 x₂ тонн бензина 1- го сорта. Следовательно, должно быть: 0,6 x₁ + 0,8 x₂ = 50.

Расход бензина второго сорта на смеси A и B составляет 0,4 x₁ + 0,2 x₂ тонн, то есть 0,4 x₁ + 0,2 x₂ = 30.

Итак, получили систему:



Решаем ее методом Крамера:



Таким образом, из 50 тонн бензина 1-го сорта и 30 тонн бензина 2-го сорта образуют 70 т смеси A и 10 т смеси B .

Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. - Электронный курс. - М: МИЭМП, 2007. - 
Режим доступа к курсу: http://e-college.ru. - П. 6.4.

2.2. По формулам Крамера решить систему: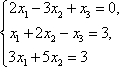



Решение: Определитель 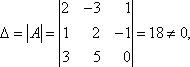  следовательно, по теореме Крамера система имеет единственное решение. Вычислим определители матриц Δ₁, Δ₂, Δ₃, полученных из матрицы A заменой соответственно первого, второго и третьего столбцов столбцом свободных членов: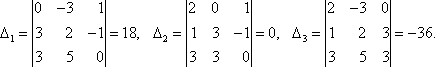



Теперь по формулам Крамера :



Ответ: (1; 0; –2).

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 36.

Тема 3. Ранг и базисные строки матрицы

1. Рангом матрицы A (rang А или r (А)) называется наивысший порядок отличных от нуля миноров этой матрицы.

2. Свойства ранга матрицы:

а) если матрица А имеет размеры m × n , то rang A ≤min (m; n);

б) rang A = 0 тогда и только тогда, когда все элементы матрицы А равны 0;

в) если матрица А — квадратная порядка n, то rang A = n тогда и только тогда, когда |А| ≠ 0.

3. Элементарные преобразования, не меняющие ранга матрицы:

а) отбрасывание нулевой строки (столбца);

б) умножение всех элементов строки (столбца) матрицы на число, не равное нулю;

в) изменение порядка строк (столбцов) матрицы;

г) прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;

д) транспонирование матрицы.

4.С помощью элементарных преобразований матрицу можно привести к ступенчатому виду: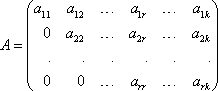



Ранг ступенчатой матрицы равен r .

5.Строки (столбцы) матрицы е₁ , е₂ , ..., е_m называются линейно зависимыми, если существуют такие числа λ₁ , λ₂ , …, λ_m не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке: λ₁е₁ + λ₂е₂ + … + λ_mе_m , где 0 = (0, 0, …, 0). В противном случае строки матрицы называются линейно независимыми.

6. Теорема о ранге матрицы:

Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов.

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 19–20.

Определение. Рангом матрицы называется число ненулевых строк в ее ступенчатом виде.

Ранг матрицы A обозначается r (A) = rang (A). Ранг матрицы не меняется при элементарных преобразованиях и не зависит от способа приведения матрицы A к ступенчатому виду.

Пример. Найти ранг матрицы: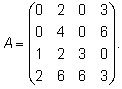



Решение. Приведем матрицу A к ступенчатому виду.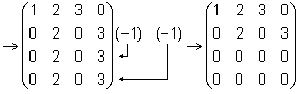





Ранг матрицы A равен двум, r (A) = rang (A). В любой матрице A с рангом r (А) = k найдутся такие k строки, что ранг матрицы, составленной их этих строк, также равен k . Такие строки матрицы A называются базисными . Если при приведении матрицы A к ступенчатому виду не использовать прибавление какой-либо строки низшей, чем данная, то базисные строки матрицы A — это в точности те строки, которые при приведении к ступенчатому виду перешли в ненулевые строки. Найдем базисные строки матрицы в последнем примере. Для этого будем отмечать ненулевые строки слева, начиная с последней матрицы (ступенчатого вида матрицы A). Затем отметим соответствующие им строки у каждой матрицы, учитывая изменение положения строк (элементарные преобразования 1-го типа). У матрицы A базисные строки 3-я и 4-я.

Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — 
Режим доступа к курсу: http://e-college.ru. — П. 6.5.

1.51. Найти ранг матрицы: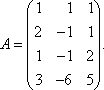



Решение. Матрица А имеет размер 4 × 3, значит, r (А) ≤ 3. С помощью элементарных преобразований, не меняющих ранг матрицы, приведем матрицу А к ступенчатому виду.

1) Транспонируем матрицу А :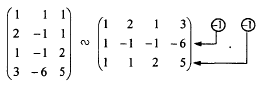



2) Умножим элементы 1-й строки на (–1), сложим ее со 2-й и 3-й строками матрицы. В новой матрице поменяем местами 2-ю и 3-ю строки:



3) Умножим элементы 2-й строки на 3 и сложим с элементами 3-й строки: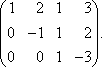



Получили ступенчатую матрицу размера 3 × 4, у которой 3 ненулевых элемента на главной диагонали, значит, r (А) = 3. Эта матрица имеет ненулевой минор 3-го порядка, например,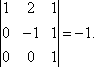



Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 20–21.

Тема 4. Операции над матрицами

Определение 8.25. Транспонированием матрицы называется такое преобразование матрицы, при котором строки и столбцы меняются ролями при сохранении номеров. Транспонированная матрица обозначается А^Т .



Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали.

Определение 8.26. Суммой (разностью) двух матриц одинакового порядка называется матрица того же порядка, каждый элемент которой равен сумме (разности) соответствующих элементов исходных матриц.



Определение 8.27. Произведением матрицы на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента исходной матрицы на это число.



Пример 8.7.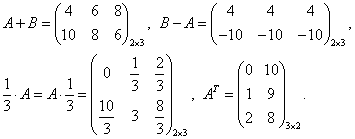 



Определение 8.28. Произведением двух матриц А и В , размеры которых заданы соотношением: количество столбцов первой матрицы равно количеству строк второй, называется матрица С , у которой количество строк равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй. Каждый элемент данной матрицы равен сумме попарных произведений элементов соответствующей строки первой матрицы и элементов соответствующего столбца второй.



Пример 8.8. 



Умножить В на А нельзя, так как число столбцов матрицы В не равно числу строк матрицы А .

Пример 8.9.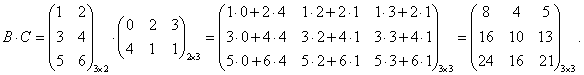 



В · С ≠  С · В. Произведение матриц не коммутативно!

Пример 8.10.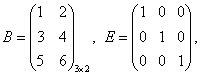 



А · Е = Е · А = А

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 127–129.

5. Возведение квадратной матрицы А в целую положительную степень m (m > 1):



Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 7.