Линейная алгебра. Тема Действительные числа

• Название: Тема Действительные числа
• Дата: 21.09.2022
• Размер: 2.01 Mb.
• Имя файла: Линейная алгебра.docx
• Тип: Закон; #689818
• страница: 2 из 8

Тема 3. Проекция вектора на ось.

Проекцией 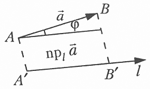  вектора   на ось l называется величина направленного отрезка А'В' (где АА'   ВВ'   — рис. 4.11), т.е. число, взятое со знаком «+», если направление А'В' совпадает с направлением оси l , и со знаком «–», если эти направления противоположны:





Рис. 4.11

Скалярным произведением   двух векторов   и   называется число, равное произведению длин этих векторов на косинус угла φ между ними:



Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 121.



Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 17.

3.4. Даны два единичных вектора   и    угол между которыми 120°.

Найти: а) острый угол между диагоналями параллелограмма, построенного на векторах   и   б) проек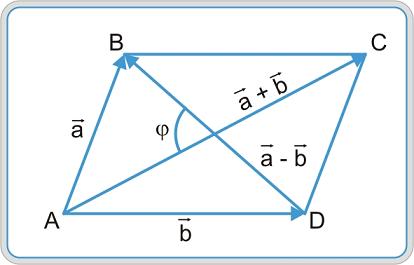цию вектора   на направление вектора    

Решение:



Рис.3.4

а) Искомый угол φ (рис. 3.4) определим по формуле (3.13):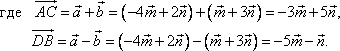





По формулам найдем скалярное произведение векторов 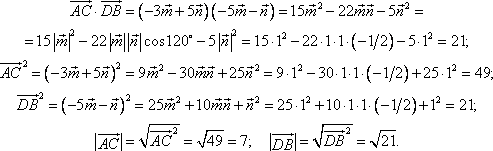  и   и их длины:



Теперь

 

и

 

б) По формуле



Найдем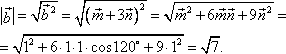





Теперь 



Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 66–67.

Пример 4.12. Даны векторы   и 

Найти: а) скалярное произведение векторов   где   б) угол между векторами   и   

Решение, а) По определению 

По формуле найдем длины векторов   и   



По формуле скалярное произведение



б) По формуле угол между векторами 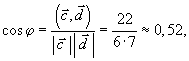  и   определяется равенством



откуда φ = arccos 0,52 » 58°.

Векторным произведением вектора    на вектор    называется вектор   удовлетворяющий условиям (рис. 4.12):

а) длина вектора   равна произведению длин векторов   и   на синус угла φ между ними, т.е.



б) вектор   перпендикулярен каждому из векторов   и 

в) вектор   направлен так, что из конца этого вектора кратчайший поворот от    к     виден против часовой стрелки (иными словами, векторы   образуют правую тройку векторов).



Рис. 4.12

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 122–123.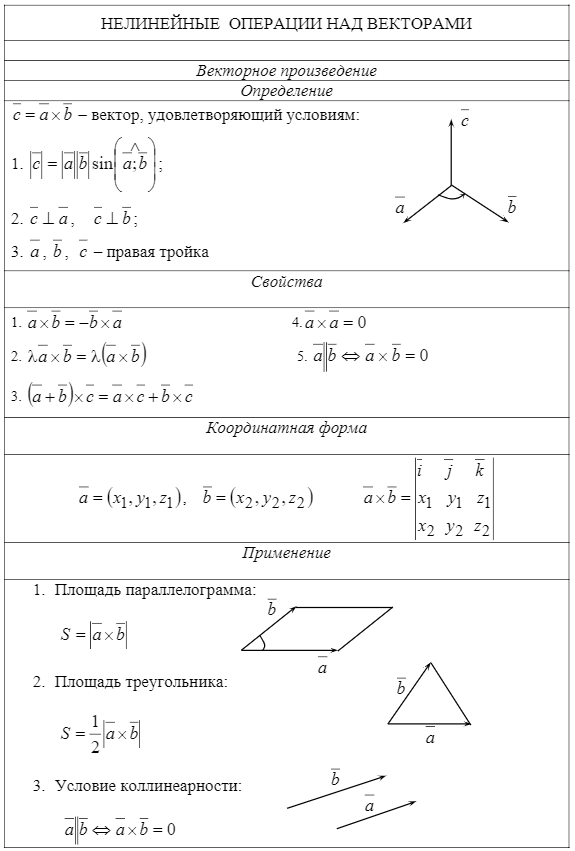



Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 18.

Примеры

1. Дано:  ,  .

Найти:  .

Решение: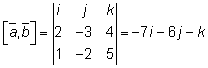

.

.

.

2. Дано:  ,  .

Найти: S sin α 

Решение: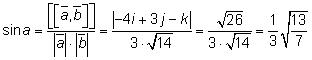



Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — 
Режим доступа к курсу: http://e-college.ru. — П. 3.3.

Смешанным произведением векторов   называется скалярное произведение векторов   и   где    есть векторное произведение векторов   и   

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 123.



Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 19.

Линейная алгебра

Тема 1. Матрицы. Определитель матрицы

Матрицы

Определение 8.18. Прямоугольная таблица чисел вида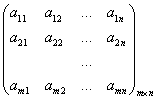



называется прямоугольной матрицей размера m × n , где m - количество строк, а n - количество столбцов.

Определение 8.19. Числа, которые образуют матрицу, - a _ij, где    называются элементами матрицы.

Определение 8.20. Числа i и j называются индексами элемента a _ij, i показывает, в какой строке расположен данный элемент, а j - в каком столбце находится этот элемент.

Две матрицы считаются равными, если равны их соответствующие элементы.

Виды матриц

Если m = n, то матрица называется квадратной матрицей порядка n .

Матрица размера m × 1 называется матрицей-столбцом.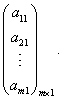



Матрица размера 1 × n называется матрицей-строкой.



Определение 8.21. Элементы матрицы, имеющие равные индексы, образуют главную диагональ матрицы.

Определение 8.22. Квадратная матрица называется диагональной, если все элементы вне ее главной диагонали равны нулю.

Определение 8.23. Диагональная матрица n -го порядка, у которой диагональные элементы равны единице, называется единичной матрицей n -го порядка и обозначается Е.

Определение 8.24. Матрица называется матрицей треугольного вида, если все элементы над (под) главной диагональю равны нулю.

Примеры.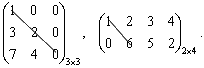 

Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 125–126.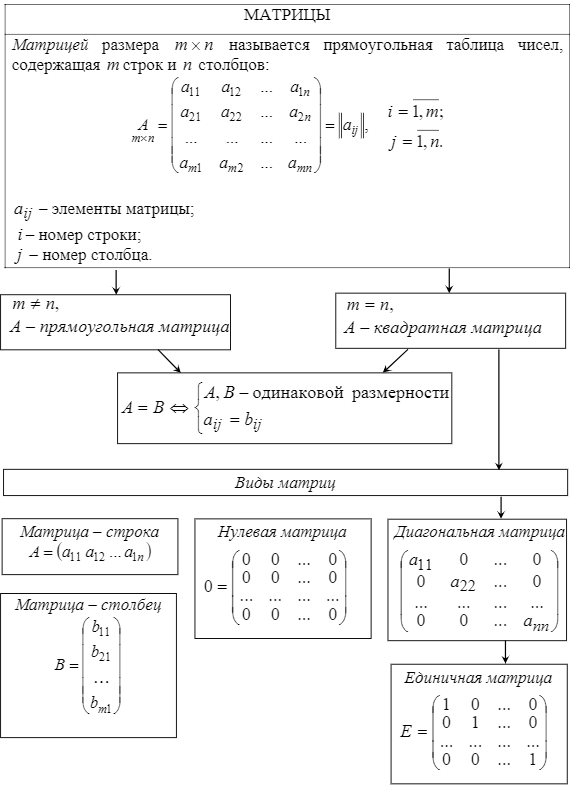





Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. - Ульяновск: ООО «Вектор-С», 2008. - С. 6, 10.

  2. Определитель квадратной матрицы 3-го порядка может быть вычислен по правилу треугольников, или правилу Сарруса.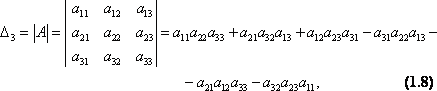



где соответствующие произведения элементов берутся либо со знаком «+» (левая схема), либо со знаком «–» (правая схема):



5.Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения:



Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 11, 12.

Свойства определителей

Теорема 8.8.При транспонировании величина определителя не меняется.

Следствие. Строки и столбцы в определителе равноправны, т. е. свойства, справедливые для строк, будут справедливы и для столбцов.

Теорема 8.9.Если все элементы одной строки определителя умножить на одно и то же число, то и весь определитель умножится на это число.

Следствие. Постоянный множитель строки можно выносить за знак определителя.

Теорема 8.10.Если в определителе поменять местами две строки, то определитель сменит знак на противоположный.

Следствие 1. Определитель, у которого две строки равны, равен нулю.

Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю.

Теорема 8.11.Если строка определителя представлена в виде алгебраической суммы нескольких слагаемых, то определитель равен алгебраической сумме определителей, у которых в первом определителе в данной строке стоит первое слагаемое, во втором - второе слагаемое и т. д.

Следствие. Если строки определителя линейно зависимы, то такой определитель равен нулю.

Теорема 8.12.Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится.

Миноры и алгебраические дополнения

Пусть дана прямоугольная матрица А размера m × n .

Определение 8.30. Минором порядка k данной матрицы, где k ≤ min (m; n), называется определитель k -го порядка, полученный из матрицы А вычеркиванием (m - k) строк и (n - k) столбцов.

Пример 8.13.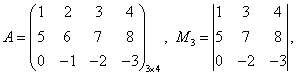





Определение 8.31. Дополнительным минором M_ij к элементу a_ij квадратной матрицы A_{n × n} называется определитель (n - 1) порядка, полученный из матрицы А вычеркиванием этого элемента вместе со строкой и столбцом, в которых он расположен.

Пример 8.14.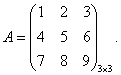

 

Найдем дополнительный минор к элементу a₃₁ . 

Определение 8.32. Алгебраическим дополнением A_ij к элементу a_ij квадратной матрицы A_{n × n} называется число A_ij = (- 1)^i+j × M_ij .

Пример 8.15. Найдем алгебраическое дополнение к элементу a₃₃ .



Теорема 8.13.Определитель равен сумме попарных произведений элементов любой строки (столбца) на их алгебраические дополнения.

  - разложение определителя по i -й строке.

Теорема 8.14.Сумма попарных произведений элементов любой строки (столбца) определителя на алгебраические дополнения к соответствующим элементам другой строки (столбца) равна нулю.

Вычисление определителей порядка n > 3 сводится к вычислению определителей второго и третьего порядка с помощью теорем 8.12 и 8.13.

Пример 8.16.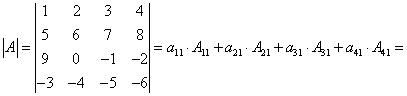



разложение определителя по первому столбцу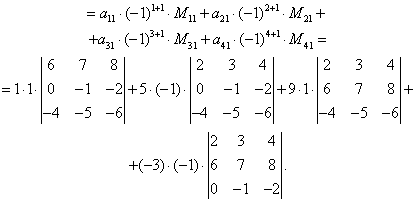



Перед разложением определителя для удобства получают в одном из столбцов нули. Это сокращает объемы вычислений. Для этого используют теорему 8.12. Одну из строк умножают на некоторые числа и складывают с другими строками.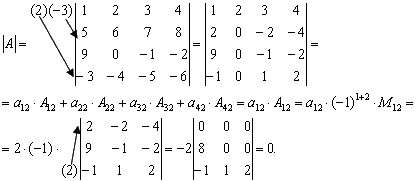



Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 131–134.

1.24.  Вычислить определители матрицы A :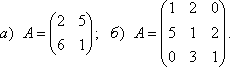



Решение:

а) По формуле 

б) Определитель вычисляется по формуле (1.8). Запоминать эту формулу не следует, достаточно применить правило треугольников, согласно которому три произведения элементов, показанных на левой схеме (п. 2), берутся со знаком «+», а три других произведения элементов, показанных на правой схеме (п. 2), берутся со знаком «–»

| A |  =  1  ×   1  ×   1  +  0  ×   2  ×   2  +  0 ×  5 ×  3 – 0 ×  1 ×  0 – 1 ×  2 ×  3 – 1 ×  2 ×  5 = –15.

1.25. Вычислить тот же определитель, приведенный в задаче 1.24 , б , используя его разложение по элементам: а ) первой строки; б ) второго столбца.

Решение:

а) Находим алгебраические дополнения элементов первой строки по формуле  :



Теперь по теореме Лапласа (1.10) :

| A |  = a₁₁   ×  A₁₁   + a₁₂   ×  A₁₂   + a₁₃   ×  A₁₃  = 1 ×  (– 5) + 2 ×  (– 5) + 0 ×  15 = –15.

б) Находим алгебраические дополнения элементов второго столбца:



Теперь по формуле (1.8) :

| A |  = a₂₁   ×  A₂₁   + a₂₂   ×  A₂₂   + a₃₂   ×  A₃₂   =  2  ×   (– 5)  +  1  ×   1  –  3  ×   2  =  –15.

1.26. Вычислить определитель матрицы четвертого порядка: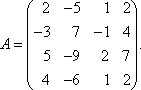



Решение: С помощью эквивалентных преобразований приведем матрицу A к треугольному виду. Если возможно, перестановкой строк (столбцов) добиваемся того, чтобы элемент a₁₁   =  1. В данном случае достаточно поменять местами 1-й и 3-й столбцы; при этом меняется знак определителя матрицы A :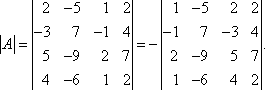



Умножая элементы 1-й строки на числа (–a_ij); i = 1, 2, 3, 4, т.е. в данном случае на числа 1, (–2), (–1), и прибавляя их соответственно к элементам 2-й, 3-й и 4-й строк, добиваемся того, чтобы все элементы 1-го столбца (кроме a₁₁) равнялись нулю: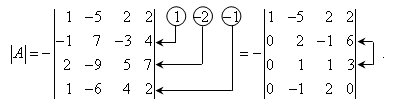



Далее, если возможно, перестановкой строк (столбцов) добиваемся, чтобы новый элемент a₂₂   =  1. В данном случае это возможно, если переставить 2-ю и 3-ю строки; при этом меняется знак определителя. Умножая элементы 2-й строки, полученной матрицы на числа (–a₁₂) (i = 3, 4), в данном случае на числа (–2) и 1, добиваемся того, чтобы все элементы 2-го столбца (кроме a₂₂) равнялись нулю.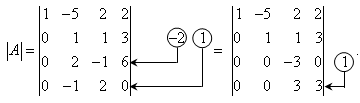



Для получения треугольной матрицы в данном случае достаточно прибавить элементы 3-й строки полученной матрицы к элементам 4-й. Определитель треугольной матрицы равен произведению ее диагональных элементов: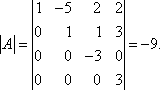

 

Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 13–14.