Последний вариант цифровой электроники. Последний вариант цифровой электроники (1). Тема Математическое введение в цифровую технику. 11
 Скачать 2.28 Mb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| j | A | B | C | F |
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
Конкретная комбинация значений аргументов носит название набора. Каждый набор имеет индекс j, численно равный десятичному эквиваленту двоичного числа.
ФАЛ от одной и двух переменных принято называть элементарными. Эти функции имеют специальные названия и обозначения и используются при воспроизведении более сложных логических функций. В таблице 1.4 приведены все возможные переключательные функции двух переменных.
Таблица 1.4.
| fj | X: | 0 | 0 | 1 | 1 | Название функции | Обозначение функции |
| Y: | 0 | 1 | 0 | 1 | |||
| f0 | | 0 | 0 | 0 | 0 | константа 0 | 0 |
| f1 | | 0 | 0 | 0 | 1 | конъюнкция X и Y | X×Y; X&Y; XÙY |
| f2 | | 0 | 0 | 1 | 0 | функция запрета по Y | XDY |
| f3 | | 0 | 0 | 1 | 1 | переменная X | X |
| f4 | | 0 | 1 | 0 | 0 | функция запрета по X | YDX |
| f5 | | 0 | 1 | 0 | 1 | переменная Y | Y |
| f6 | | 0 | 1 | 1 | 0 | функция неравнозначности (сложение по модулю два) | XÅY |
| f7 | | 0 | 1 | 1 | 1 | дизъюнкция X и Y | XÚY, X+Y |
| f8 | | 1 | 0 | 0 | 0 | стрелка Пирса | X¯Y |
| f9 | | 1 | 0 | 0 | 1 | функция равнозначности | XY |
| f10 | | 1 | 0 | 1 | 0 | инверсия Y |  |
| f11 | | 1 | 0 | 1 | 1 | импликация от X к Y | X®Y |
| f12 | | 1 | 1 | 0 | 0 | инверсия X |  |
| f13 | | 1 | 1 | 0 | 1 | импликация от Y к X | Y®X |
| f14 | | 1 | 1 | 1 | 0 | штрих Шеффера | XïY |
| f15 | | 1 | 1 | 1 | 1 | константа 1 | 1 |
Для аналитической записи переключательных функций используются вспомогательные функции, называемые конституентой единицы и конституентой нуля. Конституентой единицы n переменных называется такое булево произведение (конъюнкция) этих переменных, в которое каждая переменная входит только один раз в прямой или инверсной форме. Переменная, принимающая на данном наборе единичное значение, записывается в конституенте единицы в прямом виде, а отрицательное – в инверсном виде. Отличительной особенностью конституенты единицы является то, что она равна «1» только на одном, вполне определенном наборе значений переменных. Будем обозначать конституенту единицы символом mj, где индекс j указывает на номер набора, на котором конституента единицы становится равной «1». Аналогично конституента нуля есть булево сложение (дизъюнкция) n логических переменных, которое обращается в «0» лишь при одном наборе аргументов. При этом в прямом виде в конституенте нуля будет записываться переменная, принимающая на данном наборе нулевое значение, а в инверсном – единичное значение.
Аналитическая запись функции осуществляется по таблице истинности. Непосредственно из данных таблицы находится так называемая совершенная дизъюнктивная нормальная форма булевой функции (СДНФ) по выражению:
,где fj - значение функции на j-ом наборе, mj - конституента единицы, равная «1» только на одном j-ом наборе, - символ логического сложения (дизъюнкции), аналогичный символу алгебраического сложения å.
Для записи выражений в совершенной конъюктивной нормальной форме (СКНФ) используют формулу:
,где fj - значение функции на j-ом наборе, nj - конституента нуля, равная «0» только на одном j-ом наборе, - символ логического произведения (конъюнкции), аналогичный символу алгебраического произведения .
Проиллюстрируем СДНФ и СКНФ переключательной функции на примере булевой функции 3-х переменных, заданной таблицей 1.3. Формула для любой СДНФ функции 3-х переменных будет иметь вид:
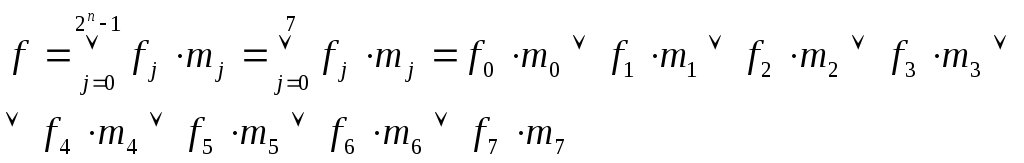
Подставляя из таблицы значения функций f0¸f7, получаем:
Формула для любой СКНФ функции 3-х переменных будет иметь вид:
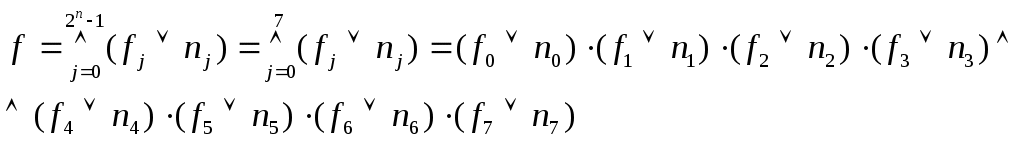
Подставляя из таблицы значения функций f0¸f7, получаем:
Аналогично находятся СДНФ и СКНФ любой другой булевой функции, заданной таблично.
Аналитическая запись ФАЛ, а также ее дальнейшие тождественные преобразования с целью получения оптимального вида опираются на следующие основные законы и тождества алгебры логики:
переместительный закон XÚY=YÚX, X×Y=Y×X;
сочетательный закон XÚ(YÚZ)=(XÚY)ÚZ, X×(Y×Z)=(X×Y)×Z;
распределительный закон X×(YÚZ)=X×YÚX×Z, X×YÚZ=(XÚZ)×(YÚZ);
закон отрицания (правило де Моргана)
, 
;закон двойного отрицания
;закон идемпотентности XÚX=X, 1ÚX=1, 0ÚX=X,
X×X=X, 1×X=X, 0×X=0;
закон склеивания XÚ
, 
;закон поглощения Y×XÚX=X; (YÚX)×X=X;
константы
Иногда вместо аналитической формы используют запись логической функции в виде последовательностей десятичных чисел. Такая запись является аналогом таблиц истинности и СДНФ или СКНФ, но при этом является гораздо более компактной. При этом в скобках указывают десятичные эквиваленты двоичных кодов конституент единицы или нуля, или, что одно и то же, номера наборов функции f, в которых она принимает единичные или нулевые значения. При указании номеров наборов с единичными значениями функции перед скобкой слева указывается знак дизъюнкции
или 
, а с нулевыми – знак конъюнкции 
или 
. В качестве примера запишем функцию, заданную таблицей 1.3 в виде десятичных чисел на единичных и нулевых наборах:f(A,B,C)=
(0,2,3,7)= (0,2,3,7);f(A,B,C)=
(1,4,5,6)= (1,4,5,6).В случае автоматизированного проектирования логических схем электронных цифровых устройств на ЭВМ ФАЛ удобно записывать в виде кубических комплексов. Такая форма в силу ограниченного числа символов позволяет формализовать запись логических функций большого числа переменных. Каждый набор переменных представляется в виде n-мерного вектора, где n – количество входных переменных. Вершины этого вектора образуют вершины n-мерного куба. Если функция задана тремя переменными, то она образует трехмерный куб, который легко представляется геометрически в виде объемной фигуры. Все единичные вершины куба, в которых функция f принимает значение «1», образуют множество нулевых кубов, называемое нулевым кубическим комплексом К0. Нулевой кубический комплекс записывается набором двоичных кодов входных переменных, для которых функция принимает единичные значения. Вершины, расположенные на концах ребер куба, называются соседними и отличаются только одной переменной. Если два куба, для которых функция равна «1», являются соседними, то они образуют куб более высокого порядка. Так, если два нулевых куба комплекса К0 являются соседними, т.е. отличаются только одной переменной, то они образуют единичный куб, геометрически представляющий ребро исходного n-мерного куба. Набор единичных кубов образуют единичный кубический комплекс К1. Записывается единичный кубический комплекс в виде набора двоичных кодов совпадающих переменных, а вместо несовпадающих проставляются прочерки. Аналогично соседние единичные кубы, отличающиеся только одной переменной, образуют двоичные кубы, набор которых в свою очередь образуют двоичный кубический комплекс К2 и т.д.
Рассмотрим запись ФАЛ в виде кубических комплексов на примере функции, заданной таблицей 1.3. Поскольку функция определяется тремя переменными, то ее можно представить трехмерным кубом (рис. 1.1). Вершины этого куба сформированы таким образом, чтобы каждая переменная, входящая в уравнение, располагалась в одной оси базиса трехмерного пространства X-Y-Z. В оси Х располагается переменная А, в оси Y – переменная В и в оси Z – переменная С. Окружностями отмечаем вершины куба, в которых функция принимает значения единицы. Эти вершины (нулевые кубы) образуют нулевой кубический комплекс К0=(000, 010, 011, 111). Из рисунка наглядно видны соседние вершины, в которых нулевые кубы отличаются только одной переменной. Ребро исходного куба, образованное соседними вершинами, выделяем толстой линией. Эти ребра образуют единичные кубы, в записи которых вместо несовпадающих переменных ставятся прочерки. Набор единичных кубов образует единичный кубический комплекс К1=(0-0, 01-, -11).
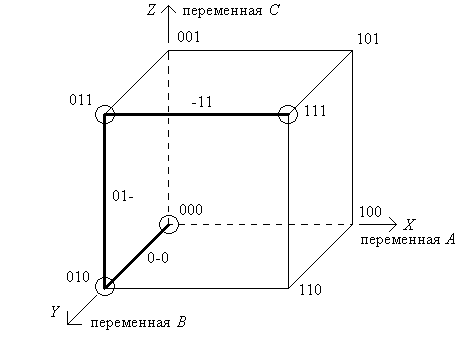
Рис. 1.1. Кубические комплексы функции, заданной таблицей 1.3.
Единичный кубический комплекс для рассмотренного выше примера является максимально возможным. Для некоторых произвольных функций трех переменных может оказаться возможным выделение двоичных кубов, образующих двоичный кубический комплекс К2. Геометрически такие кубы образовывают грани исходного трехмерного куба. В записи двоичных кубов будет присутствовать значение одной совпадающей переменной и два прочерка для несовпадающих, например, (-1-). Для функции n переменных существует теоретическая вероятность нахождения (n-1) кубических комплексов. Совокупность всех кубических комплексов образует кубический комплекс ФАЛ: К(f)=
(К0, К1, …, Кm), где m – максимально возможный кубический комплекс функции n переменных.Для выражения ФАЛ от многих переменных достаточно иметь ограниченное число разнотипных элементарных переключательных функций, называемое системой. Как показано выше, любая функция алгебры логики может быть записана в виде СДНФ или СКНФ. Следовательно, любую функцию аргументов можно представить с помощью системы только из трех элементарных функций: инверсия, дизъюнкции и конъюнкции.
Система функций алгебры логики называется функционально полной, если любая функция от произвольного числа аргументов n может быть представлена с помощью этих функций. Полная система функций называется базисом. Минимальным базисом называется такой базис, для которого удаление хотя бы одной из функций, образующих этот базис, превращает систему функций в неполную. Так, полная система из дизъюнкции, конъюнкции и инверсии может быть сокращена, поскольку с помощью формул де Моргана можно представить либо конъюнкцию через инверсию и дизъюнкцию, либо дизъюнкцию через инверсию и конъюнкцию. Таким образом, базис из дизъюнкции, конъюнкции и инверсии не является минимальным. Поскольку ни дизъюнкция, ни конъюнкция не могут быть выражены через инверсию и наоборот, то базисы, состоящие из инверсии и дизъюнкции и из инверсии и конъюнкции, являются минимальными.
Возможны различные базисы и минимальные базисы, отличающиеся числом входящих в них функций и их видом. Приведем примеры функционально полных систем:
конъюнкция, дизъюнкция, инверсия;
конъюнкция, инверсия;
дизъюнкция, инверсия;
стрелка Пирса;
штрих Шеффера.
Выбор минимального базиса связан с выбором стандартного набора логических элементов, из которых будет строиться конкретное цифровое устройство. Очевидно, что уменьшение числа функций, входящих в базис, соответствует уменьшению числа различных логических элементов, принятых за стандартные. Однако уменьшение типов стандартных элементов может привести к увеличению их общего числа. Таким образом, сложность цифрового устройства зависит не только от вида реализуемой функции, но и от вида функций, выбранных в качестве базиса.
1-4. Минимизация функций алгебры логики.
Переключательные функции являются математическими моделями некоторых реальных электронных цифровых схем. Для того чтобы синтезировать наиболее оптимальное цифровое устройство (например, имеющее минимальные аппаратные затраты), математическую модель этого устройства, представленную в виде СДНФ или СКНФ, преобразуют к соответствующему виду с использованием приведенных выше законов алгебры логики. Преобразование СДНФ или СКНФ логической функции к минимальному виду аналитической записи называется процессом минимизации ФАЛ. Однако результат минимизации функции с помощью законов и тождественных преобразований булевой алгебры во многом зависит от опыта разработчика и не всегда является очевидным. Поэтому разработан ряд алгоритмов, формализующих и автоматизирующих подобные преобразования.
Рассмотрим один из алгоритмов минимизации, предложенный американский ученым Вейчем. Вейч предложил специальные диаграммы-карты, в которые можно записать все конституенты единицы, входящие в СДНФ (конституенты нуля, входящие в СКНФ) той или иной булевой функции. На рис. 1.2 в качестве примера приведены диаграммы для минимизаций функций двух, трех и четырех переменных соответственно.
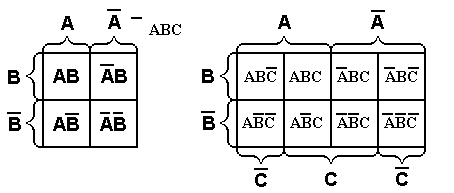
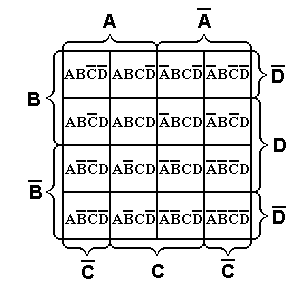
Рис. 1.2. Диаграммы Вейча для функций 2-х, 3-х и 4-х переменных.
Каждой клетке диаграммы в случае минимизации СДНФ соответствует определенная конситуента единицы. Метод минимизации с помощью диаграмм Вейча заключается в следующем. Конституенты единицы, входящие в СДНФ булевой функции, заносятся в соответствующие клетки диаграммы. Удобно наличие соответствующей конституенты единицы изображать в клетке диаграммы цифрой 1, а отсутствие - 0. Все диаграммы построены таким образом, что рядом расположенные единицы по горизонтали или вертикали склеиваются между собой в соответствии с законом склеивания алгебры логики. Одну и ту же конституенту единицы можно использовать для склеивания с несколькими другими конституентами единицы с целью получения наиболее простого окончательного выражения. Цель всех операций - получить как можно меньшее число прямоугольников (в том числе квадратов), чтобы число членов СДНФ уменьшилось, получив в итоге МДНФ.
Формировать прямоугольники можно только при включении в них хотя бы одного нового члена. Склеивание можно осуществлять и путем замыкания крайних ребер в «бочку». Таким образом, полученная диаграмма Вейча геометрически образует цилиндр. На рис. 1.3 приведены некоторые правила склеивания конституент единицы для функций 2-х и 3-х переменных.
Поскольку для ФАЛ трех переменных диаграмма представляет как бы развертку цилиндра, разрезанного по
, поэтому единицы, расположенные по краям диаграммы (например, как это изображено на рис. 1.3) считаются расположенными рядом.Метод минимизации СДНФ с помощью диаграмм Вейча включает в себя следующие шаги:
производится занесение в соответствующую диаграмму конституент единицы, входящих в СДНФ минимизируемой функции;
используя приведенные выше правила склеивания, находят простые импликанты функций (простой импликантой называется некоторая конъюнкция, полученная в результате склеивания конституент единицы, не участвующая в склеивании ни с одной другой из конъюнкций);
находится искомая минимальная дизъюнктивная нормальная форма (МДНФ) ФАЛ выбором минимальной совокупности простых импликант, покрывающей все конституенты единицы диаграммы.
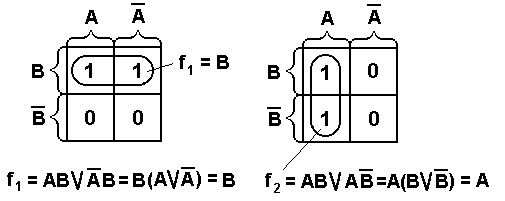
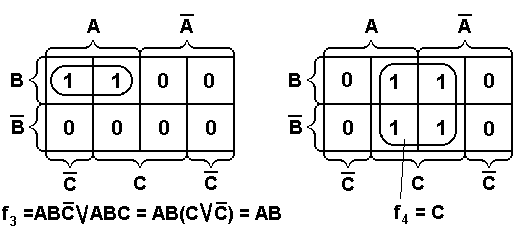
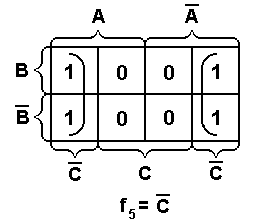
Рис. 1.3. Примеры для иллюстрации правил склеивания.
В качестве примера найдем МДНФ функции, заданной таблицей 1.3. Диаграмма Вейча этой функции представлена на рис. 1.4. Из рисунка видно, что в результате склеивания образовались две простые импликанты:
и 
. Импликанта 
участвует в склеивании с конъюнкциями и и поэтому не является простой. Таким образом, полученная МДНФ имеет вид 
. В истинности полученного выражения можно убедиться путем подстановки всех наборов переменных А, В и С.
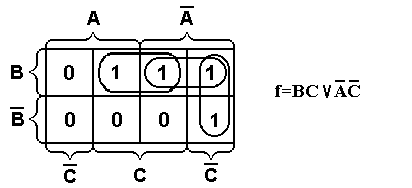
Рис. 1.4. Пример минимизации функции, заданной таблицей 1.3.
Аналогом диаграмм Вейча являются карты Карно. Они позволяют изображать на плоскости прямоугольника конституенты единицы (нуля) для ФАЛ более четырех переменных. В отличие от диаграмм Вейча, в которых отдельным строкам и столбцам соответствуют отдельные переменные, в картах Карно им можно присваивать значения нескольких переменных. При этом должны быть представлены все возможные комбинации этих переменных, например:
, 
, и 
. Таким образом, общее количество переменных минимизируемой с помощью карты Карно ФАЛ может быть больше, чем в случае использования диаграмм Вейча. Сам процесс минимизации аналогичен описанному на примере диаграмм Вейча.Минимизация ФАЛ методом диаграмм Вейча и карт Карно в силу своей наглядности широко используется при ручном процессе минимизации логических функций от небольшого количества переменных, обычно не превышающего пяти. В случае, когда количество переменных больше, необходимо использовать методы, характеризующиеся однозначностью алгоритма, что позволяет автоматизировать процесс минимизации на ЭВМ. Одним из таких методов является метод Квайна и Мак-Класки. Суть метода состоит в следующем:
все конституенты единицы, записанные в виде двоичных кодов, разбиваются на группы, содержащие одинаковое количество единиц;
склеивание производят между конституентами единицы, расположенными только в соседних группах, т.е. в соседних кубах кубического комплекса функции f;
все склеенные конституенты, образующие импликанты, отмечают каким-либо признаком, например звездочкой;
не отмеченные при склеивании импликанты являются простыми и заносятся в импликантную матрицу, в первой строке которой записываются все конституенты единицы функции f, а в первом столбце – все простые импликанты;
в пересечении строк и столбцов импликантной матрицы проставляется звездочка (или другой выделяющий символ) в тех местах, где соответствующая импликанта покрывает конституенту единицы;
ищутся столбцы импликантной матрицы, имеющие только по одной звездочке;
соответствующие этим звездочкам простые импликанты называются базисными и образуют ядро функции f и обязательно входят в МДНФ;
рассматриваются столбцы импликантной матрицы и выделяются те, которые содержат более одной звездочки;
если среди выделенных столбцов существуют такие, которые покрываются базисными импликантами из ядра функции, то они считаются уже учтенными в записи МДНФ, если же выделенные столбцы базисными импликантами не покрываются, то в МДНФ записываются импликанты соответствующих столбцов с минимальным количесвом переменных.
Рассмотрим пример минимизации функции f, заданной таблицей 1.3 методом Квайна и Мак-Класски. Функция принимает единичные значения при следующих значениях переменных А, В и С - 000, 010, 011, 111, которые и образуют конституенты единицы. Эти конституенты можно записать в четыре группы по количеству в них единиц:
группа 0: 000 *;
группа 1: 010 *;
группа 2: 011 *;
группа 3: 111 *.
Осуществим склеивание конституент из соседних групп. Те конституенты, которые удается склеить, пометим звездочкой. Результатом склеивания являются импликанты, которые аналогично записываются в группы по количеству в них единиц. Вместо несовпадающих разрядов в записи импликант проставляются прочерки:
группа 1: 0-0;
группа 2: 01-;
группа 3: -11.
Дальнейшее склеивание соседних импликант возможно только при наличии прочерка в одинаковых позициях. В нашем примере это условие не выполняется и, поэтому, образованные импликанты являются простыми. Из полученных простых импликант составляется импликантная матрица, в первой строке которой записываются все конституенты единицы, а в первом столбце – все простые импликанты. Звездочкой отмечаются все пересечения строк и столбцов, в которых импликанты покрывают конституенты единицы.
| Простые импликанты | Контституены единицы | |||
| 000 | 010 | 011 | 111 | |
| 0-0 | * | * | | |
| 01- | | * | * | |
| -11 | | | * | * |
В матрице находим столбцы, содержащие по одной звездочке. Это столбцы с конституентами 000 и 111. Одиночным звездочкам в них соответствуют импликанты 0-0 и –11. Эти импликанты являются базисными, образуют ядро логической функции и обязательно входят в состав МДНФ. Далее выделяются столбцы, содержащие более одной звездочки. Такими столбцами являются столбцы с контитуентами 010 и 011. Поскольку эти конституенты покрываются импликантами 0-0 и –11 из ядра функции, то импликанта 01- является лишней и в МДНФ не входит. В результате имеем в составе МДНФ импликанты 0-0 и-11. Заменив двоичные коды полученных импликант на обозначения переменных в прямом и инверсном виде, получим окончательную запись МДНФ функции:
, что соответствует результату минимизации методом диаграмм Вейча.Рассмотрим пример минимизации ФАЛ четырех переменных методом Квайна и Мак-Класски. Пусть задана функция в виде последовательности десятичных чисел:
.Запишем конституенты единицы функции f в виде двоичных кодов:
.Разобьем все конституенты единицы по группам из количества единиц.
группа 0: ;
группа 1: 0001 **, 0010 ***;
группа 2: 0011 ****, 0101 **, 0110 **, 1010 ***;
группа 3: 0111 ****, 1011 ***, 1110 **;
группа 4: 1111 ***.
Произведем склеивание конституент из соседних групп, помечая склеиваемые конституенты звездочками. Полученные импликанты разобьем по группам:
группа 1: 00-1 *, 0-01 *, 001- **, 0-10 **, -010*;
группа 2: 0-11 ***, -011 **, 01-1 *, 011- **, 101- *, 1-10 **;
группа 3: -111 *, 1-11 **, 111- *.
Продолжим дальнейшее склеивание импликликант из соседних групп, причем склеивание возможно только между импликантами с прочерками в одинаковых позициях:
группа 1: 0--1, 0--1, 0-1-, -01-, 0-1-, --10, -01-;
группа 2: --11, --11, -11-, 1-1-, 1-1-.
Перепишем, оставив только неповторяющиеся импликанты:
группа 1: 0--1, 0-1- *, -01- *, --10 *;
группа 2: --11 *, -11- *, 1-1- *.
Продолжим склеивание:
Группа 1: --1-, --1-, --1-.
Не отмеченные звездочками импликанты являются простыми: 0--1 и --1-. Построим импликантную матрицу:
| Простые импликанты | Контституены единицы | |||||||||
| 0001 | 0010 | 0011 | 0101 | 0110 | 0111 | 1010 | 1011 | 1110 | 1111 | |
| 0--1 | * | | * | * | | * | | | | |
| --1- | | * | * | | * | * | * | * | * | * |
Из матрицы видно, что столбцы, содержащие по одной звездочке соответствуют обеим простым импликантам и, следовательно, обе эти импликанты являются базисными, образуют ядро ФАЛ и входят в МДНФ. Заменяя двоичные коды импликант соответствующими переменными, запишем вид МДНФ:
. В истинности полученного выражения можно убедиться подстановкой всех возможных значений входных переменных A, B, C, и D.При минимизации частично определенной ФАЛ недостающие наборы выбираются произвольно исходя из соображения получения наименьшего количества простых импликант, по возможности содержащих минимальное количество переменных. На диаграмме Вейча такие импликанты будут определяться максимально большими прямоугольниками. Поэтому при минимизации частично определенной ФАЛ в диаграмму Вейча заносят все определенные значения функции в виде соответствующих нулей и единиц. В неопределенных ячейках дописываются нули и единицы до образования максимально склеиваемых областей, соответствующих простым импликантам с наименьшим количеством переменных. Например, если для заданной функции трех переменных заполненная диаграмма Вейча имеет вид (прочерками указываются неопределенные значения), представленный на рис. 1.5,а, то после дополнения единиц в позициях
и 
, диаграмма Вейча примет вид, представленный на рис. 1.5,б. В результате склеивания МДНФ запишется 
.
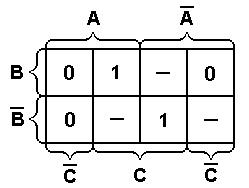
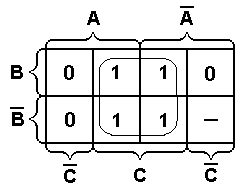
а) б)
Рис. 1.5. Пример минимизации частично определенной ФАЛ.
Контрольные вопросы.
1. Дайте определение системы счисления и приведите примеры используемых в цифровой технике систем счисления.
2. Отнимите из числа 5710 число 8310 и из числа 8310 число 5710 по правилам двоичной арифметики, используя дополнительные коды и операцию сложения.
3. Дайте определение функции алгебры-логики. Приведите различные формы записи для произвольной логической функции трех переменных.
4. Выполните минимизацию логической функции из предыдущего вопроса, используя диаграммы Вейча и метод Квайна и Мак-Класски.
5. Изобразите кубические комплексы произвольной логической функции двух переменных геометрической фигурой.