Последний вариант цифровой электроники. Последний вариант цифровой электроники (1). Тема Математическое введение в цифровую технику. 11
 Скачать 2.28 Mb.
|
|
8.3. Типовые КЦУ. Любое КЦУ и логическую часть цифрового измерительного устройства вообще можно реализовать с использованием комбинационных микросхем малой степени интеграции. Однако при разработке узлов цифровых устройств существует класс типовых широко применяемых КЦУ со стандартными функциями, уже реализованных в виде интегральных микросхем. Такие микросхемы относятся к микросхемам средней степени интеграции и в сочетании с микросхемами малой степени интеграции применяются при реализации более сложных функций в цифровых схемах измерительных устройств. Перейдем к рассмотрению типовых комбинационных устройств. 8.3.1 Дешифраторы и шифраторы. Дешифратор – это устройство, предназначенное для преобразования двоичного кода в напряжение логической единицы (логического нуля) на том выходе, номер которого совпадает со значением двоичного кода на входе. Иными словами дешифратор преобразует двоичный код в унитарный. Унитарным называется код, в котором единица присутствует только в одном разряде, а в остальных - нули. При n входах в полном дешифраторе имеется m=2n выходов, т.е. для каждой комбинации входных сигналов имеется соответствующий выход. Дешифратор, у которого при n входах число выходов меньше чем 2n, называется неполным. Другое название дешифратора - декодер. Часто количество входов и выходов дешифратора формулируют записью «из n в m». Принцип работы полного трехразрядного дешифратора рассмотрим на примере его таблицы истинности (таблица 8.4). Обычно выходы дешифратора реализуют в инверсном виде. В скобках в таблице для такого случая указаны инверсные значения выходных функций. Таблица 8.4
Соответствующие таблице истинности ФАЛ для прямых и инверсных значений выходных функций соответственно имеют вид                 .Функциональная схема трехразрядного дешифратора, синтезированная на основе полученных ФАЛ для прямых значений выходных функций приведена на рис. 8.7,а, а для инверсных - на рис. 8.7,б. Условные графические обозначения дешифратора «из 3 в 8» в электрических функциональных и принципиальных схемах приведены на рис.8.8. Часто для обозначений входов и выходов в дополнительном поле УГО микросхемы проставляют весовые или разрядные коэффициенты соответствующих систем счисления. Т.е. для трех двоичных входов дешифратора такие весовые коэффициенты будут иметь обозначения «1», «2» и «4», а для семи выходов унитарного кода - соответствующие разрядные коэффициенты десятичной системы счисления «0», «1», …, «7». 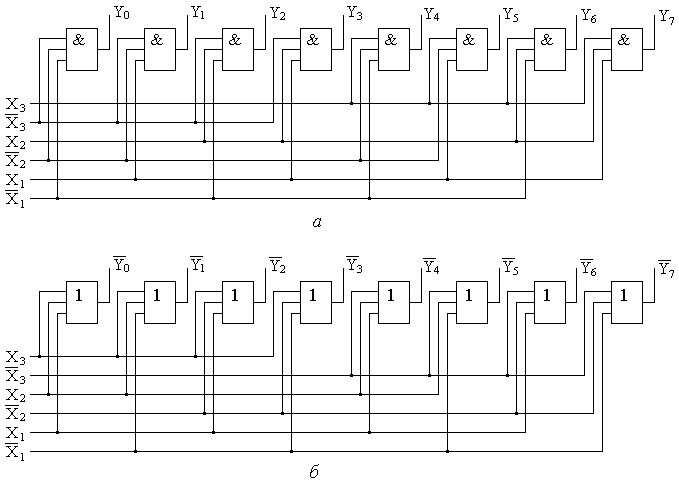 Рис. 8.7. Функциональная схема трехразрядного дешифратора с прямыми (а) и инверсными (б) выходами. 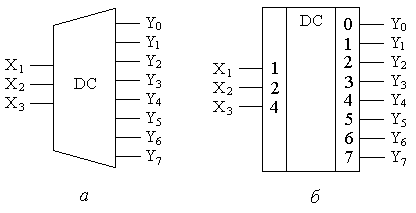 Рис. 8.8. Условное графическое обозначение дешифратора «из 3 в 8» на функциональных (а) и принципиальных (б) схемах. В общем случае логические уравнения для прямых и инверсных значений выходных переменных дешифратора на n входов имеют вид         ……… ………   .Построенные по полученным формулам дешифраторы с использованием n-входовых элементов И или ИЛИ называются линейными. К преимуществу линейных дешифраторов можно отнести высокое быстродействие, поскольку входные переменные одновременно поступают на все элементы. Одновременно, без дополнительных задержек, формируется и результат на выходах этих элементов. В существующих микросхемах элементов И и ИЛИ количество входов ограничено обычно восемью. Следовательно, ограничена и разрядность реализуемых на их основе линейных дешифраторов, что является недостатком. Указанного недостатка лишены пирамидальные дешифраторы или, как их еще называют, многоступенчатые. Принцип построения этих дешифраторов состоит в применении только двухвходовых элементов. Сначала строят линейный дешифратор первой ступени для двухразрядного числа X1, X2 из четырех двухвходвых элементов И, как это показано на рис 8.9. Затем полученные конъюнкции объединяют элементами И с переменной X3 в прямом и инверсном видах, образуя вторую ступень дешифратора. Наращивая таким образом структуру, можно построить пирамидальный дешифратор на произвольное число входов. Для этого каждая следующая ступень должна содержать в два раза большее количество двухвходовых элементов по сравнению с предыдущей. Общее количество ступеней должно быть на единицу меньшим, чем разрядность входного двоичного кода. Для пирамидальных дешифраторов n-разрядного слова требуется большее количество двухвходовых логических элементов, чем для линейных дешифраторов такой же разрядности n-входовых. Однако следует иметь в виду, что количество логических элементов, располагаемых в одном корпусе ИС, определяется главным образом требуемым количеством выводов. Следовательно, в одном корпусе ИС можно расположить большее число двухвходовых элементов, чем трехвходовых, четырехвходовых и т.д. И значит, пирамидальная структура дешифратора по числу корпусов ИС может оказаться более предпочтительной, чем линейная. Это уже справедливо для дешифратора «из 4 в 16». Для линейной схемы необходимо было бы использовать шестнадцать четырехвходовых элементов И. Учитывая, что одна микросхема содержит два четырехвходовых элемента И, общее количество микросхем составило бы восемь штук. Для пирамидальной структуры потребовалось бы 4+8+16=28 двухвходовых элемента И. Так как в одном корпусе микросхемы содержится четыре двухвходовых элемента, то общее количество корпусов в этом случае составит 7 штук. 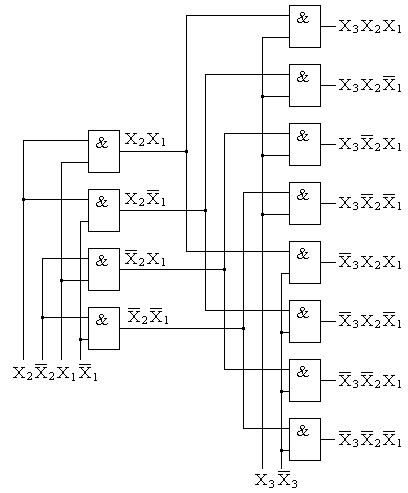 Рис. 8.9. Функциональная схема пирамидального дешифратора «из 3 в 8». Дальнейшим развитием пирамидального дешифратора является матричный дешифратор. В структуре матричного дешифратора входной двоичный код разбивается на две группы по n и m разрядов. Коды обоих групп дешифрируются двумя независимыми дешифраторами. Выходные цепи этих дешифраторов объединяются в матрицу размерностью nхm, например, как это показано на рис.8.10. В пересечениях строк и столбцов матрицы устанавливаются схемы совпадения единиц (двухвходовые элементы И), формируя унитарный выходной код разрядностью 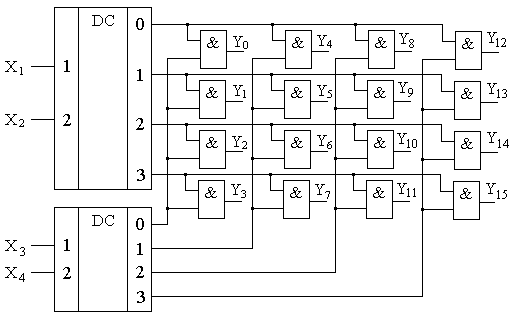 из декодированных унитарных кодов соответствующих групп разрядов n и m. Если используются дешифраторы на одинаковое количество разрядов n=m, то матрица элементов И будет квадратной, в противном случае – прямоугольной. Рис.8.10. Функциональная схема матричного дешифратора «из 4 в 16». Существующие микросхемы дешифраторов кроме информационных входов подачи двоичного кода имеют обычно управляющий вход разрешения E - enable (разрешить). При подаче на этот вход активного уровня сигнала дешифратор работает в соответствии с рассмотренными правилами. При подаче на данный вход пассивного уровня сигнала, на всех выходах дешифратора устанавливаются логические нули. Такой вход позволяется повышать разрядность дешифрируемого кода путем включения нескольких микросхем в каскадную структуру. На рис.8.11 показан пример каскадирования дешифраторов «из 2 в 4» в структуру «из 4 в 16». При логическом нуле в разряде X4 через инвертор на разрешающий вход E верхнего дешифратора подается логическая единица, в результате формируется унитарный код на выходах верхнего дешифратора Y0…Y7. На вход E нижнего дешифратора в это время подается логический ноль, что соответствует нулям на выходах этого дешифратора. При подаче логической единицы в разряде X4 дешифрация кода X1, X2, X3 осуществляется нижним дешифратором, а на выходах верхнего устанавливаются логические нули. В результате формируются разряды Y8…Y15 выходного унитарного кода. 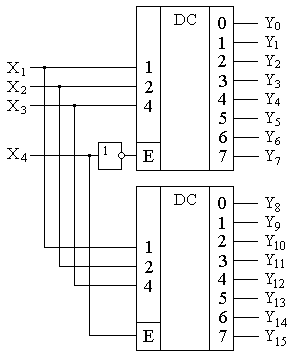 Рис.8.11. Функциональная схема каскадирования дешифраторов «из 3 в 8» в структуру «из 4 в 16». Шифраторы выполняют задачу обратную той, которую выполняют дешифраторы: появление логической единицы (логического нуля) на определенном входе из m входов приводит к появлению соответствующей кодовой комбинации на n выходах. Также как и дешифраторы, шифраторы бывают полными и неполными. Число выходов полного шифратора определяется как  . В общем случае количество входов и выходов дешифратора формулируют записью «из m в n». Работа восьмивходового полного шифратора с прямыми входами и выходами задается таблицей истинности (таблица 8.5).Таблица 8.5
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
