Последний вариант цифровой электроники. Последний вариант цифровой электроники (1). Тема Математическое введение в цифровую технику. 11

• Название: Тема Математическое введение в цифровую технику. 11
• Анкор: Последний вариант цифровой электроники
• Дата: 27.02.2022
• Размер: 2.28 Mb.
• Имя файла: Последний вариант цифровой электроники (1).doc
• Тип: Документы; #375440
• страница: 3 из 16

Тема 2. Переходные процессы в RC-цепях.
2-1. Процессы, протекающие в простейшей RC-цепи.

Переходный процесс обусловлен тем, что энергия электромагнитных полей, связанных с цепью при различных установившихся режимах различна, а скачкообразное изменение энергии, т.е. изменение энергии на конечную величину за бесконечно малый промежуток времени, невозможно из-за ограниченности величины мощности физически существующих источников энергии.

Линейным устройством (элементом) называется устройство (элемент), параметры которого не зависят от протекающего тока или приложенного напряжения. Нелинейное устройство - это устройство, параметры которого зависят от тока или напряжения.

Переходные процессы в простейших линейных цепях, т.е. в цепях RL или RC описываются дифференциальным уравнением первого порядка:
,
где x(t) - напряжение или ток в схеме, y(t) - внешнее воздействие.
Решение этого уравнения для случая y(t) = const имеет вид:
,
где t - текущее время, x(t) - напряжение или ток в схеме, x(¥) - конечное значение x(t) при t®¥, x(0) - начальное значение x(t) при t = 0.

Характер изменения функции x(t) представлен на рис. 2.1 (убывающая или нарастающая экспонента).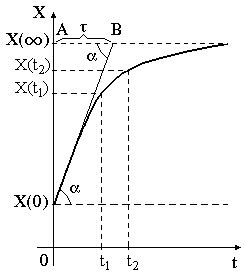

Рис. 2.1. Характер изменения экспоненциальной функции.
Выполним следующие преобразования:
,

.
Поскольку , то очевидно, что AB = t.

При анализе переходных процессов часто возникает задача нахождения интервала времени , за который функция x(t) изменяется от значения x(t₁) до значения x(t₂). Запишем значение функции в точках t₁ и t₂:
,

.
Откуда
,

,

,

,

.
Применим полученные соотношения для анализа RC-цепей. Предварительно напомним законы коммутации для RL и RC-цепей:

1-ый закон коммутации: напряжение на конденсаторе в момент коммутации не может измениться скачком U_С(0_-) = U_С(0₊);

2-ой закон коммутации: ток, протекающий через индуктивность, не может измениться скачком I_L(0_-) = I_L(0₊).

Законы коммутации являются следствием того, что энергия в цепи не может изменяться мгновенно, так как для этого требуется бесконечно большая мощность источников энергии. Рассмотрим RC-цепь (рис. 2.2).

Рис. 2.2. Схема простейшей RC-цепи.
Пусть конденсатор не заряжен и в момент времени t = 0 ключ переходит из положения «0» в положение «1». Для начальных и установившихся режимов в этом случае можно записать:

при t= 0 U_С(0) = 0, U_R(0) = E;

при t= ¥ U_С(¥) = E, U_R(¥) = 0.

После подстановки получаем:
,

.
Считая, что конденсатор заряжен до значения U_С= E, рассмотрим процесс после перевода ключа из положения «1» в положение «2». Начальные и установившиеся значения напряжений на элементах в этом случае запишутся:

при t= 0 U_С(0) = E, U_R(0) = -E;

при t = ¥ U_С(¥) = 0, U_R(¥) = 0.

После подстановки получаем:
,

.
Характер изменения функций U_C(t) и U_R(t) представлен на рис. 2.3.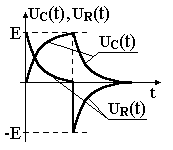

Рис. 2.3. Характер изменения функций U_С(t) и U_R(t) простейшей RC-цепи.
Из курса математики известно, что за утроенное значение постоянной времени, т.е. за время 3t, экспонента изменяется на 0.95 своего конечного полного изменения. Это значит, что за время 3t конденсатор условно разряжается и заряжается.
2-2. Интегрирующая RC-цепь.

Электрическая принципиальная схема интегрирующей RC-цепи представлена на рис. 2.4(а). Коммутация напряжения на входе, рассмотренная ранее, эквивалентна подаче на вход прямоугольного импульса напряжения (рис. 2.4(б)). Как было выведено ранее, характер изменения функции U_C(t)=U_вых в общем случае выражается следующими зависимостями: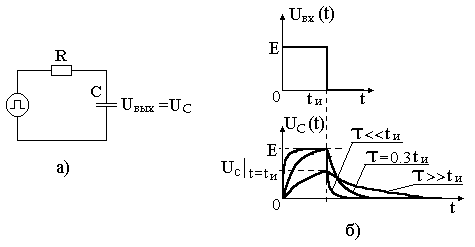
- нарастающая экспонента для 0  t  t_и;

- убывающая экспонента для t > t_и, где - значение напряжения, до которого успел зарядиться конденсатор в период действия импульса.


Рис. 2.4. Интегрирующая RC-цепь и временные диаграммы напряжений.
Разряд конденсатора после прекращения действия импульса приводит к тому, что выходной импульс будет иметь большую продолжительность, чем входной. Происходит расширение импульса без сохранения его формы, поэтому такая RC-цепь называется расширяющей.

Поскольку , а , то

.

Так как , то

.
Рассмотрим случай, когда . Поскольку , следовательно , и можно записать:
,
то есть на выходе интеграл от входного напряжения. Отсюда очевидно название рассмотренной цепи – интегрирующая. Эта цепь используется, в частности, для получения линейно изменяющегося напряжения. Для этого на вход интегрирующей цепи подается постоянное напряжение . Тогда получаем
,
то есть на выходе линейно изменяющееся напряжение (рис. 2.5).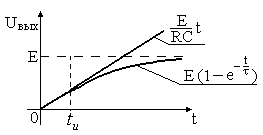

Рис. 2.5. Графики изменения идеального и реального выходных напряжений интегрирующей RC-цепи.
В отличие от рассмотренного идеального случая, в реальной цепи
.
Найдем производную по t от функции идеального выходного напряжения:
.
Аналогично для функции реального выходного напряжения производная запишется:
.
При t=0 ,
т.е. в нуле производные реальной и идеальной функций совпадают, а в дальнейшем - расходятся. За меру расхождения на интервале [0, t_и] принимают коэффициент нелинейности 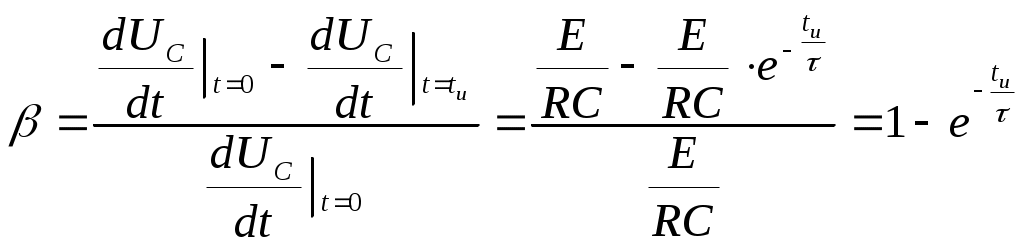- относительное изменение производной:
.
Для случая можно воспользоваться формулой разложения функции : при . Тогда
,
т.е. чем больше t при данном значении t_и, тем меньше ß. Реальная функция U_вых.р в этом случае ближе к идеальной U_вых.ид.
2-3. Разделительная дифференцирующая RC-цепь.

Электрическая принципиальная схема разделительной дифференцирующей RC-цепи и её временные диаграммы представлены на рис. 2.6.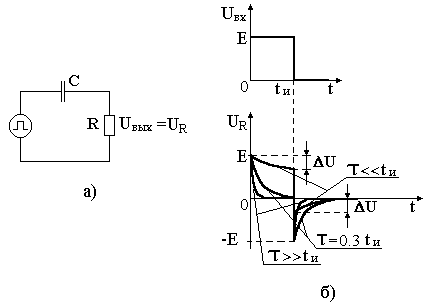


Рис. 2.6. Разделительная дифференцирующая RC-цепь и временные диаграммы напряжений.
Как было показано ранее, меняется по закону:
для 0 tt_и,

для t >t_и.
При рассматриваемая RC-цепь выполняет функции разделительной цепи, назначение которой передать входное напряжение с наименьшими искажениями и отделить при этом постоянную составляющую. Абсолютная величина завала вершины равна напряжению на конденсаторе в момент t_и снятия входного импульса, т.е.
.
Для случая 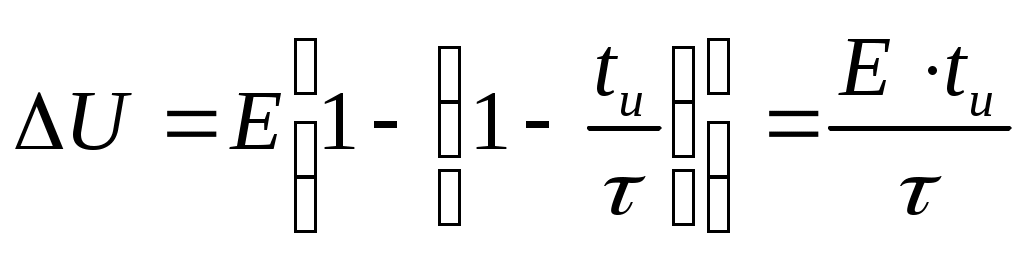, с учетом рассмотренного ранее разложения функции при получаем:
.
Оценкой качества разделительной цепи является величина относительного завала вершины , которая определяется как:
.
Таким образом, завал вершины, а значит искажение входного импульса, тем меньше, чем больше постоянная времени цепи t при данном t_и. Если величина завала вершины несравненно мала, то импульс передается без искажения.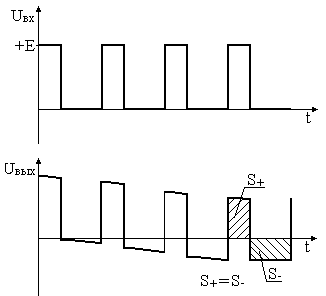

Рис. 2.7. Диаграммы входного и выходного напряжений разделительной цепи.
Из временной диаграммы рис. 2.7 видно, что амплитуда последовательности импульсов выходного напряжения постоянна, но при этом импульсы смещаются относительно нулевого уровня. В установившемся режиме площади под графиком S₊ положительной и S_- отрицательной областей последовательности импульсов окажутся равными друг другу: S₊ = S_-.

Доказать этот факт можно, рассмотрев диаграмму тока, протекающего через резистор (рис.2.8). Очевидно, что i₁t₁ - это заряд Q_и, переносимый через емкость за время действия импульса на входе, а i₂(t₂-t₁) – заряд Q_п, переносимый через емкость за время паузы между импульсами, т.е. в обратном направлении. Тогда общий заряд, переносимый через емкость за время, равное периоду импульса будет равен:
.
Поскольку постоянная составляющая через емкость не проходит 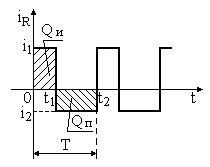, следовательно, или . Поскольку , а сопротивление – величина постоянная, то значит и равны S₊ и S_- на диаграмме U_вых. Таким образом, для разделительной цепи необходимо выполнение условия: .



Рис. 2.8. Диаграмма тока, протекающего через резистор разделительной RC-цепи.
Поскольку , а , то

Продифференцируем обе части полученного уравнения. Получим

Так как , то .
Рассмотрим случай . Поскольку , то можно записать . Тогда
.
Из полученной формулы следует название такой цепи – дифференцирующая. Для дифференцирующей цепи должно выполняться условие 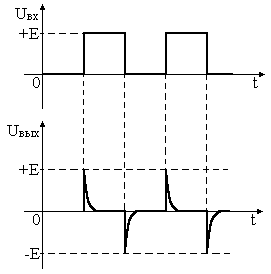, т.е. конденсатор должен успевать быстро перезаряжаться при данном t_и. Диаграммы входного и выходного напряжений дифференцирующей цепи для последовательности импульсов представлены на рис. 2.9.

Рис. 2.9. Диаграммы входного и выходного напряжений дифференцирующей RC-цепи.