Последний вариант цифровой электроники. Последний вариант цифровой электроники (1). Тема Математическое введение в цифровую технику. 11
 Скачать 2.28 Mb.
|
|
8.3.2 Мультиплексоры и демультиплексоры. Мультиплексор - комбинационное цифровое устройство, которое обеспечивает передачу на единственный выход Q одного из нескольких входных сигналов Dj в соответствии с поступающим адресным кодом Ai. При наличии n адресных входов можно реализовать m=2n комбинаций адресных сигналов, каждая из которых обеспечивает выбор одного из m входов. Как и в шифраторах (дешифраторах) количество входов и выходов мультиплексора записывают в виде «из n в 1». Правило работы мультиплексора «из 4 в 1» можно задать таблицей истинности (таблица 8.7): Таблица8.7
Логическое выражение для выходной функции, заданной таблицей, можно записать в виде  .Синтезированная по полученной ФАЛ функциональная схема мультиплексора показана на рис.8.17,а. Проанализировав ФАЛ мультиплексора можно выделить в ней составляющие минтермы дешифратора 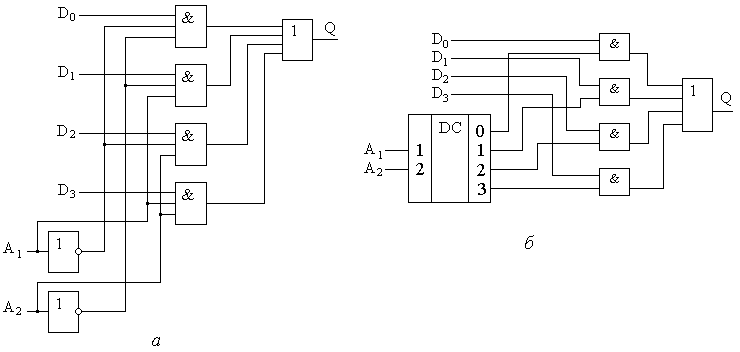 ,  ,  ,  , записанные в адресных переменных  ,  ,  ,  . Отсюда следует, что мультиплексор можно реализовать, используя дешифратор и схемы И и ИЛИ. Дешифратор формирует логическую единицу на одном из выходов согласно входному двоичному коду в соответствующем минтерме. Сигналы с выходов дешифратора объединяются схемами совпадения единиц, реализованными на двухвходовых элементах И. В результате логическая единица будет формироваться на выходе только того элемента И, на один вход которого подается логическая единица с выхода дешифратора и на второй вход – единица с соответствующего входа Dj. Для объединения минтермов мультиплексора с выходов всех элементов И в один выход Q служит элемент ИЛИ. На его выходе формируется логическая единица, если таковая присутствует на опрашиваемом в данный момент входе Dj. Функциональная схема мультиплексора на основе дешифратора показана на рис.8.17,б. Условные графические обозначения мультиплексора «из 4 в 1» в электрических функциональных и принципиальных схемах показаны на рис.8.18. Рис.8.17. Функциональная схема мультиплексора «из 4 в 1» согласно его ФАЛ (а) и на основе дешифратора (б). 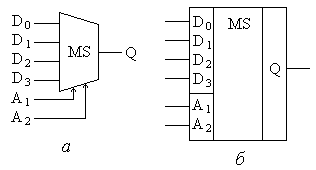 Рис.8.18. Условное графическое обозначение мультиплексора «из 4 в 1» на функциональных (а) и принципиальных (б) схемах. Мультиплесор с одним выходом называется одноканальным, а с несколькими – многоканальными с соответствующим количеством каналов. Микросхема многоканального мультиплексора содержит в одном корпусе несколько мультиплексорных структур, как правило, с общими адресными входами для всех каналов. Часто выход мультеплексора выполняют трехстабильным с возможностью перевода его в высокоимпедансное состояние. В некоторых микросхемах мультиплексоров предусматривается наличие входа стробирования. Подача на этот вход активного уровня сигнала разрешает передачу на выход одного из входных сигналов. В противном случае на выходе мультиплексора формируется логический ноль независимо от значений на его информационных и адресных входах. На базе мультиплексоров удобно строить КЦУ для реализации одной ФАЛ. Если адресные входы мультиплексора рассматривать как входные переменные ФАЛ, а на его информационные входы подать логические нули или единицы в зависимости от значений минтермов соответствующих наборов, то каждый адресный код будет вызывать коммутацию на выход мультиплексора единичного или нулевого значения ФАЛ в соответствии с таблицей истинности. На рис.8.19 приводится пример построения КЦУ на базе мультиплексора, реализующего ФАЛ, заданную таблицей 8.1. 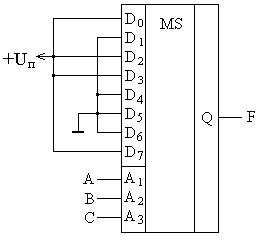 Рис.8.19. Пример реализации КЦУ на базе мультиплексора. Мультиплексоры используются для построения преобразователей параллельного кода в последовательный. Для этого на информационные входы мультиплексора подается параллельный код числа, а на адресные входы изменяющаяся на единицу последовательность двоичных кодов. Эта последовательность может быть сформирована, например, двоичным счетчиком из тактовых импульсов. В результате на выход мультиплексора будут поочередно коммутироваться значения разрядов входного параллельного кода для последующей обработки их в последовательном виде. Демультиплексор выполняет функцию, обратную мультиплексору, т.е. в соответствии с принятой адресацией Ai направляет информацию с единственного входа D на один из m выходов Qj. При этом на остальных выходах будут логические нули (единицы). Принцип работы демультиплексора «из 1 в 4» иллюстрируется таблицей истинности (таблица 8.8): Таблица 8.8.
Логические выражения для каждого из выходов можно представить в виде:     .Пример структурной схемы, реализующей демультиплексора «из 1 в 4» по записанным ФАЛ приведен на рис. 8.20,а. Анализ ФАЛ позволяет видеть, что демультиплексор, также как и мультиплексор, можно реализовать на основе дешифратора, формирующего минтермы адреса, и элементов И, стробирующих эти минтермы со значением, присутствующим на входе D (рис.8.20,б). Условные графические обозначения демультиплексора в функциональных и принципиальных электрических схемах аналогичны обозначениям мультиплексора, но его единственный вход D будет располагаться слева относительно границ УГО, а выходы Qi справа. Функция демультиплексорования задается символами «DMS» в функциональном поле УГО. Часто мультиплексоры и демультиплексоры называют коммутаторами. В маркировке микросхем функция мультиплексора и демультиплексора записывается сочетанием букв «КП». 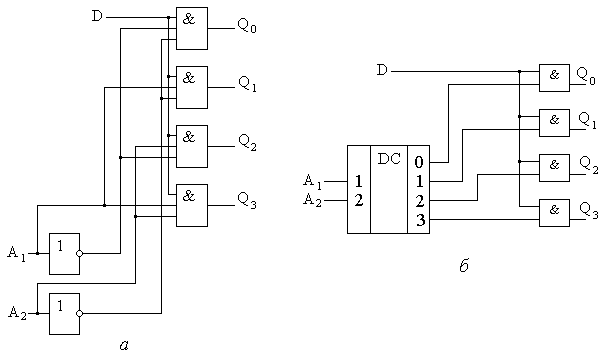 Рис. 8.20. Функциональная схема демультиплексора «из 1 в 4» согласно его ФАЛ (а) и на основе дешифратора (б). Для микросхем мультиплексоров и демультиплексоров КМОП типа каналы между входами и выходами могут образовываться ключами на базе полевых транзисторов. Т.е. при подаче определенного адреса происходит непосредственное подключение одного из входов мультиплексора на единственный выход через полевой ключ. Таким образом, для КМОП микросхемы мультиплексора смысл выводов как входов и выходов условный и зависит от применения этой микросхемы. Т.е. в качестве мультиплексора и демультиплексора может быть выбрана одна и та же микросхема. Подобные микросхемы можно использовать и как аналоговые коммутаторы униполярных сигналов, например, поступающих от нормированных датчиков различных физических величин на общий аналоговый канал измерительного прибора. Демультиплексор может также выполнять и функцию дешифратора, если на его вход подать логическую единицу (логический ноль). Мультиплексирование (демультиплексирование) при большом числе входов (выходов) можно выполнить пирамидальным каскадированием мультиплексоров (демультиплексоров), как это показано на рис.8.21. На рис.8.21,а показано каскадирование мультиплексоров «из 4 в 1» для реализации функции мультиплексирования «из 16 в 1». Мультиплексоры первого уровня управляются адресными сигналами А1 и А2, а мультиплексоры второго – адресными сигналами А3 и А4. Каждый из мультиплексоров первого уровня выбирает один из четырех разрядов Dj. Выходы с мультиплексоров первого уровня объединяются в мультиплексоре второго уровня, который осуществляет окончательную коммутацию и формирование выходного сигнала Q. По аналогичному принципу построена схема каскадного включения демультиплексторов (рис.8.21,б). Младшие разряды адреса должны подаваться на элементы низжей иерархии в обеих схемах. 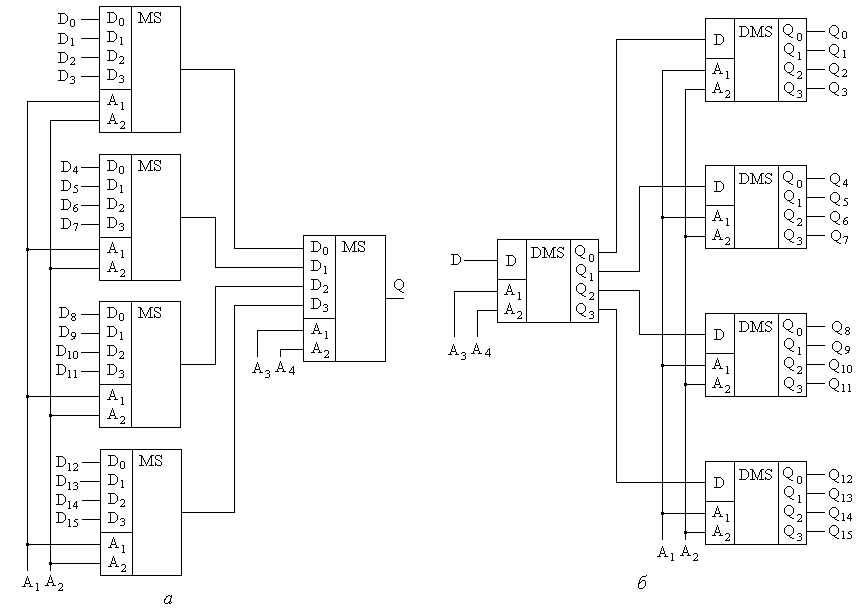 Рис.8.21. Пирамидальное каскадирование мультиплексоров (а) и демультиплексоров (б). 8.3.3 Цифровые компараторы. Цифровой компаратор предназначен для сравнения двух n-разрядных двоичных чисел A={a1, a2, ..., an} и B={b1, b2, ..., bn}. В результате сравнения может установливаться одно из соотношений: =, ≠; >; <; ≥; ≤. Выходная функция F принимает единичное значение, если проверяемое соотношение выполняется или нулевое – если не выполняется. Цифровой компаратор позволяет реализовывать ту часть алгоритма измерения в цифровой измерительной технике, в которой заложена процедура сравнения неизвестного значения измеряемой величины с цифровой мерой. Рассмотрим синтез компаратора для реализации функции равенства двух n-разрядных двоичных кодов. Факты равенства, больше и меньше отдельных разрядов определим функциями f(A=B)i, f(A>B)i и f(A<B)i, заданной следующей таблицей истинности 8.9: Таблица 8.9.
Тогда факт неравенства разрядов будет определяться инверсным значением функции  . Определим ФАЛ для f(A=B)i, соответствующую приведенной таблице истинности .Синтезированная структурная схема в соответствии с формулой для f(A=B)i имеет вид, представленный рис. 8.22. 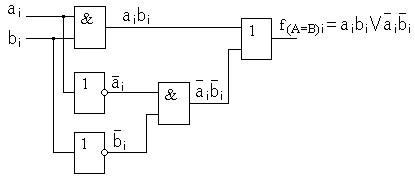 Рис. 8.22. Функциональная схема устройства сравнения одноразрядных кодов. Выполним следующие преобразования над функцией f(A=B)i, используя тождества алгебры логики:  ,т.е. окончательно имеем инверсию функции исключающее ИЛИ. Функция неравенства одного разряда тогда будет выражаться через прямое значение функции Исключающее ИЛИ. Для перехода от равенства (неравенства) отдельных разрядов к функции равенства F(A=B) (неравенства  ) всего n-разрядного кода необходимо установить факт наличия логических единиц во всех функциях f(A=B)i ( ). Это осуществляется n-входовым элементом И. ФАЛ для функции F(A=B) с учетом использования функции инверсии исключающего ИЛИ имеет вид .Функция f(A>B)i одноразрядного числа согласно таблице 8.9 будет реализовываться двухвходовым элементом И, на один вход которого будет подаваться разряд ai в прямом виде, а на второй – разряд  в инверсном виде, т.е.  . Несколько сложнее обстоит дело со схемой сравнения n-разрядных слов на «больше». Для этого анализ неравенства должен выполняться последовательно в направлении от старших разрядов в сторону младших. Младшие разряды сравниваются при условии равенства старших. Тогда логика сравнения на «больше» для двухразрядного слова с учетом равенства/неравенства старшего разряда может быть представлена в следующем виде .Аналогично можно записать логику сравнения для трехразрядного числа  и четырехразрядного числа  .В общем случае функция сравнения на «больше» для произвольного n-разрядного числа можно выразить  Подставив минтермы функций f(A>B)i в переменных ai и bi и эквивалентные функциям f(A=B)i элементы исключающее ИЛИ-НЕ, можно реализовать представленную ФАЛ для F(A>B). Функцию сравнения на «меньше» можно определить как  ,т.е. только если будет отсутствовать факт равенства F(A=B)=0 и факт больше F(A>B)=0, то схемой совпадения нулей (функцией ИЛИ) установится общий ноль, а инверсия этого нуля даст единичное значение функции F(A<B) как последнего оставшегося варианта сравнения. Пример схемы, реализующей рассмотренные выше функции F(A=B), F(A>B) и F(A<B) двух четырехразрядных чисел приведен на рис.8.23. 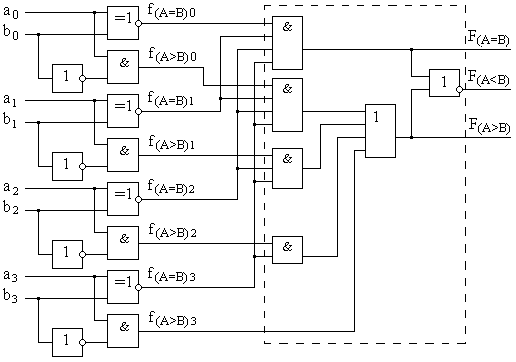 Рис.8.23. Функциональная схема компаратора, реализующего функции «равно», «больше», «меньше» двух четырехразрядных чисел. Из-за громоздкости структуры компараторов чисел большой разрядности и необходимости использования в этом случае логических элементов с большим количеством входов, в интегральном исполнении обычно реализуются компараторы, сравнивающие двоичные коды с разрядностью n не более 4 или 8 бит. Для повышения разрядности обрабатываемых кодов сравниваемые слова разбиваются на группы фиксированной разрядности с индивидуальными выходами функций сравнения на «равно»F(A=B)i и «больше» F(A>B)i в каждой группе. Тогда описанный выше метод применим и для анализа n-разрядных кодов. Для этого выходы функций равенства и больше компараторов отдельных групп объединяются в часть схемы рис.8.23, заключенную в пунктирную линию. В результате формируется результат сравнения кодов всей длины. В условном графическом обозначении функция компаратора задается символами «= =» или «COMP». В качества примера можно привести микросхему четырехразрядного компаратора К561ИП2, реализующую функции сравнения на «больше», «меньше» и «равно». Эта микросхема может также применяться для сравнения кодов большей разрядности (рис.8.24). Для этого в ней предусмотрены входы переноса функций «меньше» и «равно», на которые подаются выходы одноименных функций группы младших разрядов. Вход «больше» в данной микросхеме избыточен, и на него в микросхемах всех групп необходимо постоянно подавать потенциал логической единицы. На вход «меньше» микросхемы самой младшей группы необходимо подать логический ноль, а на вход «равно» - логическую единицу. Такое же включение микросхемы должно быть и при использовании ее для сравнения четырехразрядных слов. 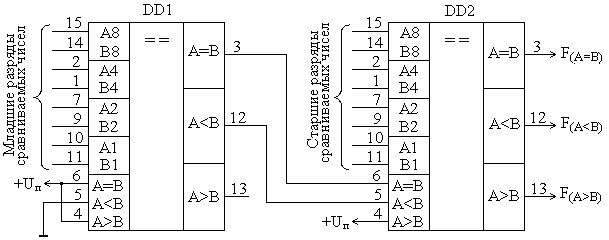 Рис.8.24. Включение микросхемы К561ИП2 при повышения разрядности сравниваемых слов. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||