Последний вариант цифровой электроники. Последний вариант цифровой электроники (1). Тема Математическое введение в цифровую технику. 11
 Скачать 2.28 Mb.
|
|
СДНФ для переменных S и P одноразрядного полного сумматора после ряда тождественных преобразований следующие:  , .Выражение 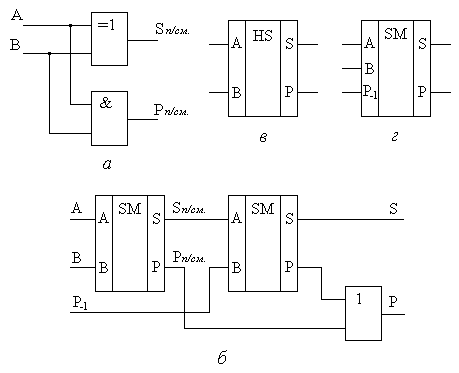 есть ни что иное, как значение выхода переноса полусумматора над величинами Sп/см. и Р-1. Учитывая этот факт и анализируя полученные логические уравнения, можно сделать заключение о возможности реализации полного сумматора на основе двух полусумматоров и одного элемента ИЛИ. Схема полного одноразрядного сумматора представлена на рис. 8.25,б, а УГО одноразрядных полусумматора и сумматора соответственно на рис. 8.25,в и рис.8.25,г. Рис.8.25. Схема функциональная одноразрядного полусумматора на элементах «исключающее ИЛИ» и конъюнкторе (а), полного одноразрядного сумматора на базе двух полусумматоров (б), УГО одноразрядных полусумматора (в) и полного сумматора (г). Схему полного сумматора можно также реализовать и на вентилях элементарных функций в базисе И-ИЛИ-НЕ. Из таблицы истинности 8.11 полного одноразрядного сумматора очевидно, что на выходе суммы S формируется единица, а на выходе переноса Р – ноль при наличии единицы на одном из входах A, B или Р-1. При наличии единиц на любых двух из трех входов полного сумматора, на выходе S будет ноль, а на выходе P – единица. При наличии на всех трех входах логических единиц, на обоих выходах сумматора присутствуют единицы. При нулях на всех трех входах выходы также принимают нулевые состояния. Структура, реализующая описанное правило и положенная в основу микросхем сумматоров 155 и 555 серий, приведена на рис. 8.26. 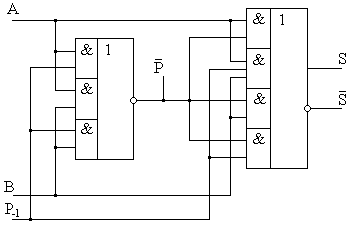 Рис. 8.26. Функциональная схема одноразрядного полного сумматора в базисе И-ИЛИ-НЕ. При суммировании многоразрядных двоичных чисел с помощью одноразрядных сумматоров их соединяют в последовательные структуры, как это показано на рис.8.27. В этой схеме переносы передаются последовательно путем соединения выходов переносов 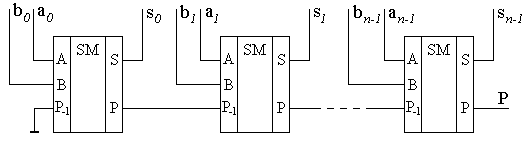 одноразрядных сумматоров младших разрядов с входами переносов  одноразрядных сумматоров старших разрядов. Вход переноса одноразрядного сумматора самого младшего разряда заземляется, что равносильно подаче на него логического нуля. Такой способ наращивания разрядности достаточно прост в схемной реализации, но при этом имеет существенный недостаток – низкое быстродействие. Общее время срабатывание схемы всего сумматора будет равно времени срабатывания одного сумматора, умноженного на количество разрядов. Таким образом, чтобы не считать ошибочный код, считывание информации с устройства возможно только по прошествии указанного времени. Рис. 8.27. Схема функциональная сумматора с последовательной передачей переноса. Существет способ организации структуры многоразрядного сумматора, в которой переносы во все разряды формируются одновременно с подачей входных кодов складываемых чисел. Т.е. переносы подаются на все входы одновременно или, иными словами, параллельно. Поэтому такая структура получила название сумматора с параллельным переносом. Выражение для переноса в старший разряд одноразрядного полного сумматора можно преобразовать к следующему виду   Введем обозначения  и  , где gi – функция переноса, hi – функция передачи переноса. Тогда .В общем случае можно записать  ,где  - перенос в самый младший разряд из предыдущего сумматора, если таковой предусмотрен в структуре цифрового устройства. В противном случае =0. Таким образом, сигнал pi можно получить одновременно с появлением всех разрядов аi и вi на входах сумматора, не дожидаясь формирования переноса в отдельных разрядах полных одноразрядных сумматоров. В случае четырехразрядных чисел А и В можно записать , , .Для построения четырехразрядного сумматора с параллельным переносом необходимо полученные ФАЛ для pi каждого разряда реализовать в каком-либо базисе, например И-НЕ. Далее выходные сигналы pi с каждой части такой комбинационной схемы должны быть поданы на соответствующие входы Р-1 полных одноразрядных сумматоров. Пример такой структуры приведен на рис. 8.28. 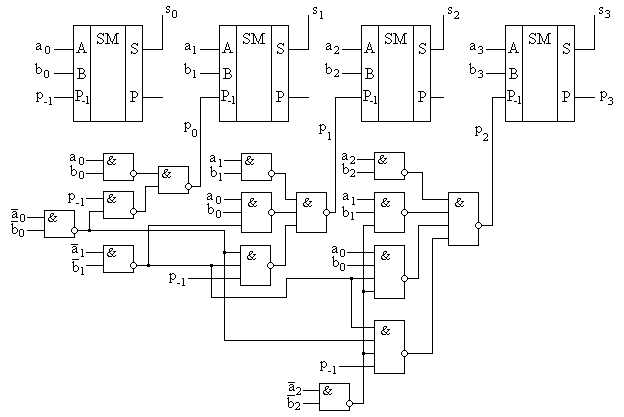 Рис. 8.28. Схема функциональная четырехразрядного сумматора с параллельным переносом. Из рисунка видно, что даже для четырехразрядного сумматора требуется достаточно сложная комбинационная схема формирования переноса. Поэтому схемы сумматоров с параллельным переносом в интегральном исполнении реализуют обычно для сложения чисел с разрядностью не более четырех бит. При необходимости реализации быстродействующих сумматоров для сложения двоичных чисел большей разрядности используют два подхода. Первый заключается в использовании микросхем полных сумматоров с параллельным переносом в качестве базовых элементов и объединении их в общую последовательную структуру. Сумматоры, реализованные по такой структуре, называются сумматорами с цепным переносом. Подобная структура не может обладать максимальным быстродействием, но при этом является простой в схемотехнической реализации. Второй подход также основан на использовании набора микросхем сумматоров с параллельным переносом. Но их объединение в общую структуру основано на принципе параллельной передачи переноса. В этом случае требуется дополнительная комбинационная схема, реализующая параллельный перенос между параллельными сумматорами. Сумматоры с такой структурой называются параллельно-параллельными. Они имеют максимальное быстродействие, но их реализация требует дополнительных аппаратных затрат. Сумматор является основой для многих схем выполнения арифметических операций над двоичными и двоично-десятичными кодами. Кроме собственно суммирования, сумматоры используются в перемножителях. Умножение в двоичном коде выполняется аналогично умножению десятичных чисел – столбиком. Приведем в качестве примера выполнение умножения столбиком двух трехразрядных двоичных чисел: 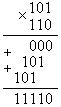 Из примера видно, что умножение реализуется операциями суммирования и сдвига. Существует несколько методов построения умножителей. Наиболее проста в схемотехнической реализации матричная организация перемножителя на базе сумматоров, показанная на рис.8.29. Эта схема иллюстрирует построение умножителяля трехразрядных положительных двоичных чисел. Для формирования произведения трехразрядных двоичных чисел требуется вычислить три частичных произведения. Обратите внимание, что в двоичной арифметике требуется выполнять умножение только на числа 0 и 1. Поскольку в одном разряде правила выполнения арифметического и логического умножений совпадают, то для формирования частичного произведения можно воспользоваться логическими элементами «2И». 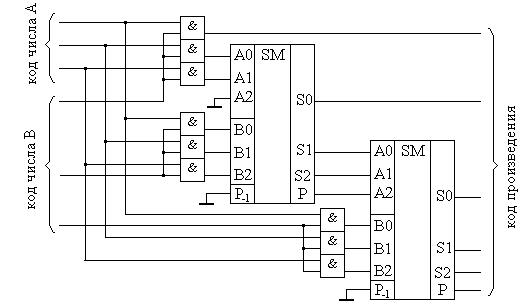 Рис.8.29. Схема матричного перемножителя трехразрядных двоичных положительных чисел. Для формирования частичного произведения, кроме операции умножения на один разряд, требуется осуществлять его сдвиг влево на число разрядов, соответствующее весу разряда множителя. Сдвиг можно осуществить простым соединением соответствующих разрядов частичных произведений к необходимым разрядам двоичных сумматоров. Первый сумматор суммирует первое и второе частные произведения. При этом самый младший разряд первого частного произведения согласно примеру не нуждается в суммировании. Поэтому он подаётся на выход умножителя непосредственно. А два остальных разряда первого частного произведения подаются на входы A первого сумматора со смещением вправо на один разряд. На свободный старший разряд входов A первого сумматора достаточно подать незначащий ноль (т.е. просто заземлить этот вход). Второе частное произведение подается на входы B первого сумматора без смещения. Точно таким же образом осуществляется суммирование третьего частного произведения. Отличие заключается только в том, что на старший разряд входов A второго сумматора подается сигнал переноса с выхода первого сумматора. Таким образом, сдвиг в схеме матричного перемножителя осуществляется за счет смещения на один разряд частных произведений и подачи их на входы сумматоров следующих разрядов с номерами, на единицу меньшими. 8.3.5 Преобразователи кодов. В цифровой измерительной аппаратуре важное место занимают преобразователи кодов. По определению и по сути преобразователем кодов является любое КЦУ, поскольку как и КЦУ, преобразователь кодов преобразует n-разрядный входной код в m-разрядный выходной. Частным случаем преобразователей кодов можно рассматривать шифраторы и дешифраторы, выполняющие преобразование десятичного кода в двоичный и обратно. Однако существует класс устройств, традиционно относящихся по своим функциональным свойствам к категории преобразователей кодов. Распространенность использования преобразоветелей кодов можно объяснить тем, что они позволяют аппаратно реализовывать функции преобразования кодов с устройств ввода-вывода, т.е. с максимальным быстродействием. Использование преобразователей кодов часто можно встретить даже в измерительной и управляющей аппаратуре на базе микропроцессорной и микроконтроллерной техники. Несмотря на усложнение при этом электрической схемы устройства, повышение быстродействия и получение более простой управляющей программы делает использование преобразователей кодов оправданным. В общем случае функция преобразования кодов задается в функциональном поле УГО элемента обозначением «X/Y», где X – входный код, а Y – выходной. В каждом конкретном случае, если это возможно, желательно вместо X и Y указывать конкретные обозначения, например, «2/2-10» для преобразователя двоичного кода в двоично-десятичный. Часто требуется вводить информацию в цифровую систему с привычных для человека десятичных устройств, например с кнопочных клавиатур из десяти кнопок. Задача такого преобразования легко решается с помощью шифраторов. Пример организации подобного решения был рассмотрен ранее. Но, поскольку обработка информации в цифровом устройстве реализуется обычно по правилам двоичной арифметики и результат представлятся в двоичном коде, то для вывода результата на десятичные устройства, например, на десятичные индикаторы, система вывода инфорации должна быть снабжена двоично-десятичным преобразователем. Преобразователи двоично-десятичных кодов выполняют преобразование чисел, представленных в двоичной системе счисления, в двоично-десятичные числа и обратно в соответствии с таблицей 8.12 на примере преобразования их десятичных эквивалентов в диапазоне значений от 0 до 63. Таблица 8.12
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||