4.7. Разложение булевой функции по переменным
Пусть s принимает значения 0 или 1, т.е. s {0, 1}. {0, 1}.
Введем обозначение: обозначение:
xs = x, если s = 0, xs = x, если s = 1.
Т.е. x0 = x, x1 = x.
Очевидно, что xs = 1, если x = s и xs = 0, если x 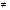 s. s.
Теорема 4.5 (о разложении булевой функции по переменным).
Каждая булева функция f(x1, x2, ... , xn) может быть представлена в виде:
f(x1, x2, ... , xn) = f(x1, x2, ... , xm, xm+1, ... , xn) =
V x1s1&x2s2&...&xmsm& f(s1, s2, ... sm, xm+1, ... , xn), (4.1)
m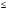 n, где дизъюнкция берется по всем наборам (s1, s2, ... , sm) (их 2m). n, где дизъюнкция берется по всем наборам (s1, s2, ... , sm) (их 2m).
Например, для m = 2, n = 4 разложение (4.1) включает в себя четыре (2m = 22 =4) конъюнкции и имеет вид:
f(x1, x2, x3, x4) = x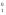 &x &x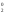 &f(0, 0, x3, x4) V x &f(0, 0, x3, x4) V x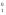 &x &x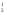 &f(0, 1, x3, x4) V x &f(0, 1, x3, x4) V x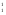 & x & x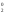 &f(1, 0, x3, x4) V x &f(1, 0, x3, x4) V x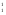 & x & x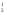 &f(1, 1, x3, x4) = x1&x2&f(0, 0, x3, x4) V x1&x2&f(0, 1, x3, x4) V x1&x2&f(1, 0, x3, x4) V x1&x2&f(1, 1, x3, x4). &f(1, 1, x3, x4) = x1&x2&f(0, 0, x3, x4) V x1&x2&f(0, 1, x3, x4) V x1&x2&f(1, 0, x3, x4) V x1&x2&f(1, 1, x3, x4).
Доказательство теоремы 4.5.
Теорема будет доказана, если показать, что равенство (4.1) выполняется для произвольного набора переменных (y1, y2, ... , ym, ym+1, ... , yn) .
Подставим этот произвольный набор переменных в левую и правую части равенства (4.1).
В левой части получим f (y1, y2, ... , yn) .
Т. к. ys = 1 только, когда y = s, то среди 2m конъюнкций y1s1&y2s2&...&ymsm в правой части (4.1) только одна обратится в 1 – та, в которой y1 = s1,…, ym = sm. Все остальные конъюнкции равны 0. Поэтому в правой части (4.1) получим:
y1y1&y2y2&...&ymym&f(y1, y2, ... , ym, ym+1, ... , yn) = f(y1, y2, ... , yn) .
Теорема 4.5 доказана.
Теорема 4.6 (о представлении булевой функции формулой в СДНФ),
Всякая булева функция f(x1, x2, ... , xn),не равная тождественно 0, может быть представлена формулой в СДНФ, которая определяется однозначно с точностью до перестановки дизъюнктивных членов.
Доказательство.
При m = n получим важное следствие теоремы 4.5:
f(x1, x2, ... , xn) = V x1s1&x2s2&...&xnsn, (4.2)
f(s1, s2, ... , sn) = 1
где дизъюнкция берется по всем наборам (s1, s2, ... , sn), на которых f = 1.
Очевидно, что разложение (4.2) есть не что иное, как СДНФ формулы f, которая содержит столько конъюнкций, сколько единиц в таблице значений f. Следовательно, СДНФ для всякой булевой функции единственна с точностью до перестановки ее дизъюнктивных членов.
Очевидно также, что для булевой функции f(x1, x2, ... , xn), тождественно равной 0, разложение (2) не существует.
В силу изложенного для получения формулы булевой функции f(x1, x2, ... , xn) в СДНФ можно воспользоваться следующим алгоритмом.
Алгоритм 4.3. (Алгоритм представления булевой функции, заданной таблицей, формулой в СДНФ).
Шаг 1. Выбираем в таблице все наборы переменных s1, s2, ... , sn, для которых значение f равно 1, т. е. f (s1, s2, ... , sn) = 1.
Шаг 2. Для каждого такого набора (строки таблицы) составляем конъюнкцию x1s1&x2s2&...&xnsn, где xisi = xi, если si = 1 и xisi =xi, если si = 0, i = 1, 2, ... ,n.
Шаг 3. Составляем дизъюнкцию всех полученных конъюнкций. В результате получится формула данной функции в СДНФ.
Пример 4.15.
Найдем формулу в СДНФ для функции f(x1, x2, x3), заданной таблицей 4.4.
1. Выберем в таблице строки, где f(x1, x2, x3) =1. Это 4-ая, 5-ая. 6-ая и 8-ая строки.
2. Для каждой выбранной строки составляем конъюнкции по правилу, указанному в шаге 2. Получим соответственно для четырех выбранных строк:
x10&x21&x31 = x1 &x2&x3.
x11&x20&x30 = x1&x2&x3.
x11&x20&x31 = x1&x2&x3 .
x11&x21&x31 = x1&x2&x3 .
3. Составляем дизъюнкцию всех полученных конъюнкций и находим СДНФ:
f(x1, x2, x3) = x1&x2&x3V x1&x2&x3 V x1&x2&x3 V x1&x2&x3.
Убеждаемся, что это выражение совпадает с полученным ранее в примере 4.13 представлением нашей формулы в СДНФ.
Замечание. Если булева функция задана формулой в СДНФ, то, применяя алгоритм 4.3 в обратной последовательности, легко можем получить таблицу значений этой функции.
Теорема 4.7 (о представлении булевой функции формулой в СКНФ),
Всякая булева функция f(x1, x2, ... , xn),не равная тождественно 1, может быть представлена формулой в СКНФ, которая определяется однозначно с точностью до перестановки дизъюнктивных членов.
Доказательство.
Рассмотрим функцию f(x1, x2, ... , xn). В соответствии с теоремой 4.6, если она не равна тождественно 0, существует ее формула в СДНФ. Обозначим эту формулу F1. Очевидно, условие, что функция f(x1, x2, ... , xn) не равна тождественно 0, равносильно условию, что функция f(x1, x2, ... , xn) не равна тождественно 1. Кроме того, по закону де Моргана формула F2 F1 находится в СКНФ (отрицание конъюнкции есть дизъюнкция отрицаний). По закону двойного отрицания
F2 F1 f(x1, x2, ... , xn) f(x1, x2, ... , xn),
что и доказывает теорему.
Для получения формулы булевой функции f(x1, x2, ... , xn) в СКНФ следует воспользоваться следующим алгоритмом.
Алгоритм 4.4. (Алгоритм представления булевой функции, заданной таблицей, формулой в СКНФ)
Шаг 1. Выбираем в таблице все наборы переменных s1, s2, ... , sn, для которых значение f (s1, s2, ... , sn) = 0.
Шаг 2. Для каждого такого набора (строки таблицы) составляем дизъюнкцию
x1 s1Vx2s2V...Vxnsn, где xi si = xi, если si = 0 и xi si = xi, если si = 1, i = 1, 2, ... , n.
Шаг 3. Составляем конъюнкцию всех полученных дизъюнкций. В результате получится СКНФ.
Пример 4.16.
Найдем формулу в СКНФ для функции f(x1, x2, x3), заданной таблицей 4.4.
1. Выберем в таблице строки, где f(x1, x2, x3) = 0. Это 1-ая, 2-ая и 3-я и 7-ая строки.
2. Для каждой выбранной строки составляем дизъюнкции по правилу, указанному в шаге 2. Получим соответственно для трех выбранных строк:
x11Vx21Vx31 = x1Vx2Vx3.
x11Vx21Vx30x1Vx2Vx3.
x11Vx20Vx31 = x1Vx2Vx3.
x10Vx20Vx31 = x1Vx2V x3.
3. Составляем конъюнкцию всех полученных дизъюнкций и находим СКНФ:
f(x1, x2, x3) = x1Vx2Vx3)&(x1Vx2Vx3)&(x1Vx2Vx3)&(x1Vx2Vx3).
Это выражение совпадает с полученным ранее в примере 4.14 представлением нашей формулы в СКНФ.
Замечание. Т. к. всего строк в таблице функции 2n, то, если число дизъюнктивных членов в СДНФ равно p, а число конъюнктивных членов в СКНФ равно q, то p+q=2n.
Так, для функции, рассмотренной в примерах 4.15 и 4.16, n = 3, p = 4, q = 4, p + q = 8 = 23.
4.8. Минимизация формул булевых функций в классе дизъюнктивных
нормальных форм
Как было установлено выше, произвольная булева функция может быть представлена формулой в ДНФ и КНФ, причем такое представление неоднозначно. Равносильными преобразованиями можно получить формулу, содержащую меньшее число вхождений переменных. Например, две различные формулы: f1(x1, x2) = x1V x1&x2 V x2 и f2(x1, x2) = x1 V x2 равносильны, так как в силу 2-го закона поглощения (равносильность 6б из раздела 4.3) x1 V x1&x2 x1.
Но в формуле f1(x1, x2) содержится четыре вхождений переменных, а в формуле f2(x1, x2) – два.
Определение 4.10. ДНФ называется минимальной, если она содержит наименьшее общее число вхождений переменных среди всех равносильных ей ДНФ.
Определение 4.11. Импликантом булевой функции f(x1, x2, ... , xn) называется элементарная конъюнкция С, не равная тождественно 0, такая что C V f  f. Отметим, что любая конъюнкция любой ДНФ в силу закона идемпотентности (равносильность 5б) является импликантом этой функции. f. Отметим, что любая конъюнкция любой ДНФ в силу закона идемпотентности (равносильность 5б) является импликантом этой функции.
Определение 4.12. Импликант C функции f называется простым импликантом, если после отбрасывания любой переменной из C получается элементарная конъюнкция, не являющаяся импликантом функции f.
Пример 4.17.
Для функции x&yVx&zVx&y&z x&(yVz) конъюнкции x&y и x&z – простые импликанты, а x&y&z – импликант, но не простой.
Определение 4.13. Дизъюнкция всех простых импликантов булевой функции f называется сокращенной ДНФ функции f.
Для нахождения сокращенной ДНФ используется следующий алгоритм, в основе которого лежит метод Квайна.
Алгоритм 4.5. (Алгоритм Квайна построения сокращенной ДНФ).
Шаг 1. Находим для данной булевой функции f ее формулу F, находящуюся в СДНФ.
Шаг 2. Находим все простые импликанты функции f. Для этого все элементарные конъюнкции формулы F попарно сравниваем между собой. Если две элементарные конъюнкции таковы, что они имеют вид C&xi и C&xi, то выписываем конъюнкцию С. Это является следствием 1-го закона расщепления (склеивания) (равносильность 7а). Конъюнкция С содержит n - 1 вхождение переменных. Элементарные конъюнкции, для которых произошло склеивание, помечаем. После построения всех конъюнкций, включающих n - 1 вхождение переменных, вновь сравниваем их попарно, производим, если возможно, склеивание, выписываем полученные конъюнкции из n - 2 членов, помечаем склеивающиеся конъюнкции из n - 1 членов и т. д. Процесс заканчивается, когда дальнейшее склеивание невозможно. Все непомеченные элементарные конъюнкции являются простыми импликантами. Их дизъюнкция даст нам формулу F1, равносильную F, находящуюся в ДНФ и состоящую из простых импликантов, т.е. сокращенную ДНФ.
Пример 4.18.
Найдем сокращенную ДНФ функции из примера 4.4:
f(x1, x2, x3) = (x2 x3) x3)
(x1Vx2).
1. Шаг 1 был выполнен ранее (см. примеры 4.13, 4.15). СДНФ формулы f(x1, x2, x3) является формула
F(x1, x2, x3) = x1&x2&x3V x1&x2&x3 V x1&x2&x3 V x1&x2&x3.
2. Попарно сравниваем все 4 трехчленные конъюнкции (всех сравнений C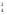 = 6) и применяем, где это возможно, закон склеивания: = 6) и применяем, где это возможно, закон склеивания:
x1&x2&x3V x1&x2&x3 = x2&x3.
x1&x2&x3 V x1&x2&x3 = x1&x2.
x1&x2&x3 V x1&x2&x3 = x1&x3.
Итак, на первом этапе получили 3 двучленные конъюнкции:
x2&x3, x1&x2, x1&x3.
Все трехчленные конъюнкции оказались помеченными.
Попарно сравниваем все 3 двучленные конъюнкции (всех сравнений 3) и замечаем, что склеивание невозможно.
В результате получим сокращенную ДНФ формулы f:
F1(x1, x2, x3) = x2&x3 V x1&x2 V x1&x3.
На практике для построения сокращенной ДНФ удобнее пользоваться модифицированным методом Квайна – Мак-Класки. Этот метод состоит в автоматизации процесса склеивания. Разберем этот метод на конкретном примере.
Алгоритм 4.6. (Алгоритм Квайна - Мак-Класки построения сокращенной ДНФ).
Шаг 1. Составим таблицу значений булевой функции (если функция задана формулой в СДНФ, то в силу замечания к алгоритму 4.3 это всегда можно сделать)
Для нашего примера такая таблица уже составлена – это таблица 4.4.
Очевидно, в силу алгоритма 4. 3 (см. также пример 4.15), эта функция имеет следующую формулу в СДНФ:
f(x1, x2, x3) = x1&x2&x3V x1&x2&x3 V x1&x2&x3 V x1&x2&x3.
Шаг 2. Выпишем наборы переменных, на которых функция принимает значение 1, причем эти наборы упорядочим по группам так, что в каждую группу входят наборы с одинаковым числом единиц. Пусть Ai – группа наборов переменных, таких, что каждый набор содержит i единиц, и функция на этом наборе переменных принимает значение, равное единице.
Группы A0 (где все переменные нули, а значение функции равно 1) нет.
Группа A1 (где одна переменная единица, остальные нули, и значение функции равно 1):
1 0 0
Группа A2:
0 1 1
1 0 1
Группа A3:
1 1 1
Шаг 3. Производим попарное сравнение наборов переменных, входящих в соседние группы. Если при этом сравнении обнаружатся два набора, которые отличаются только в одном разряде, то вместо них записывается один набор, в котором вместо несовпадающих разрядов ставится “ – “ (прочерк). После всех возможных сравнений из предшествующего списка вычеркиваются все наборы, которые участвовали в образовании хотя бы одного набора с прочерком. Формируются два массива наборов: наборы с прочерками (массив P) и невычеркнутые (массив R).
Эти действия соответствуют склеиванию конъюнкций и уменьшению числа вхождений переменных.
Для нашего примера при сравнении групп A1 и A2:
вместо (1 0 0) и (1 0 1) получим (1 0 –);
При сравнении групп A2 и A3:
вместо (0 1 1) и (1 1 1) получим (– 1 1);
вместо (1 0 1) и (1 1 1) получим (1 – 1);
После этого этапа массив R пуст, т. к. все наборы участвовали в образовании наборов с прочерками, а массив P = P(1) включает следующие наборы:
(1 0 –);
(– 1 1);
(1 – 1).
Далее рассмотрим наборы с прочерками. Они вновь попарно сравниваются между собой. При этом имеет смысл сравнивать лишь наборы, в которых прочерк стоит в совпадающих разрядах. Если сравниваемые наборы отличаются друг от друга только в одном разряде, то выписываем набор с двумя прочерками (старым и новым). После всех попарных сравнений из множества наборов с одним прочерком вычеркиваются все наборы, имеющие один прочерк и участвовавшие в образовании набора с двумя прочерками. Наборы с одним прочерком, не участвовавшие в образовании наборов с двумя прочерками, помещаются в массив R.
Для нашего примера попарное сравнение наборов с одним прочерком не приводит к образованию наборов с двумя прочерками.
Далее рассмотрим наборы с двумя прочерками и т. д. Процесс прекращается, если на очередном шаге все рассматриваемые наборы попадают в R. Нетрудно убедиться, что каждому набору из R соответствует простой импликант, причем единице соответствует переменная, взятая без отрицания, нулю – переменная, взятая с отрицанием, а прочерку – отсутствие соответствующей переменной. Сокращенная ДНФ есть дизъюнкция этих простых импликантов.
Для нашего примера процедура сравнения заканчивается после формирования наборов с одним прочерком. Массив R после этого включает наборы:
(1 0 –);
(– 1 1);
(1 – 1).
Сокращенная ДНФ имеет вид:
f(x1, x2, x3) = x2&x3 V x1&x2 V x1&x3.
Далее процесс нахождения минимальной ДНФ сводится к отбрасыванию некоторых простых импликантов.
Определение 4.14. Простой импликант называется существенным (ядровым) импликантом, если его удаление из сокращенной ДНФ функции приводит к ДНФ, которая не равносильна исходной ДНФ.
Построение минимальной ДНФ сводится к отбрасыванию несущественных импликантов из сокращенной ДНФ.
Определение 4.15. Будем говорить, что элементарная конъюнкция A покрывает элементарную конъюнкцию В, если она является частью этой конъюнкции, т.е. целиком входит в нее.
Пример 4.19.
Элементарная конъюнкция x1&x2 покрывает элементарные конъюнкции x1&x2&x3 и x1&x2&x3, но не покрывает элементарные конъюнкции x1&x2&x3 и x1&x2&x3.
Нахождение минимальной ДНФ состоит в выборе таких простых импликантов из сокращенной ДНФ, которые в совокупности покрывают все элементарные конъюнкции СДНФ и содержат минимальное число вхождений переменных. Такая ДНФ равносильна СДНФ, т. к. в силу определения 4.15 ее значения на некотором наборе переменных совпадают со значениями СДНФ.
Рассмотрим следующий алгоритм нахождения минимальной ДНФ.
Алгоритм 4.7. (Алгоритм построения минимальной ДНФ с помощью таблицы покрытий).
Шаг 1. Составление таблицы покрытий.
Дляданной функции
f(x1, x2, ... , xn) = 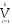 Ai Ai 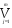 Bj, m Bj, m 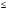 k, k,
где Ai –элементарные конъюнкции, входящие в СДНФ, i = 1, 2, ..., k, k 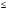 n, а Bj – простые импликанты сокращенной ДНФ, j = 1, 2, ... ,m, m n, а Bj – простые импликанты сокращенной ДНФ, j = 1, 2, ... ,m, m 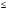 k, построим таблицу покрытий, число строк которой равно числу полученных простых импликантов, а число столбцов – числу элементарных конъюнкций в СДНФ. Если в некоторую элементарную конъюнкцию входит какой-либо простой импликант, то на пересечении соответствующего столбца и строки ставится метка (например, “ * “). k, построим таблицу покрытий, число строк которой равно числу полученных простых импликантов, а число столбцов – числу элементарных конъюнкций в СДНФ. Если в некоторую элементарную конъюнкцию входит какой-либо простой импликант, то на пересечении соответствующего столбца и строки ставится метка (например, “ * “).
Шаг 2. Выделение столбцов, содержащих одну метку.
Если в каких-нибудь столбцах составленной таблицы имеется только одна метка, то строки, в которых стоят эти метки, определяют простые импликанты, которые не могут быть исключены из сокращенной ДНФ, т. к. без них не может быть получено покрытие всех элементарных конъюнкций СДНФ. Они являются существенными и обязательно входит в минимальную ДНФ. Поэтому из таблицы покрытий исключаются строки, соответствующие существенным импликантам, и столбцы элементарных конъюнкций СДНФ, покрывемые этими существенными импликантами.
Шаг 3. Вычеркивание лишних столбцов.
Если в таблице есть столбцы, в которых имеются метки в одинаковых строках, то оставляем только один из них (все равно, какой), так как покрытие элементарных конъюнкций, соответствующих выброшенным столбцам, осуществляется за счет простого импликанта, соответствующего оставшемуся столбцу.
Шаг 4. Вычеркивание лишних существенных импликантов.
Если после выбрасывания некоторых столбцов в результате шага 3, в таблице появляются строки, в которых нет ни одной метки, то простые импликанты, соответствующие этим строкам, исключаются из дальнейшего рассмотрения, т. к. они не покрывают оставшиеся в рассмотрении элементарные конъюнкции СДНФ.
Шаг 5. Выбор минимального покрытия существенными импликантами.
Выбирается такая совокупность строк (т. е. существенных импликантов), чтобы они покрывали все оставшиеся столбцы (элементарные конъюнкции СДНФ). При нескольких возможных вариантах предпочтение отдается варианту покрытия с минимальным общим числом вхождения переменных.
Пример 4.20.
Продолжим предыдущий пример.
1. Составляем таблицу покрытий. Для формулы, булевой функции с СДНФ:
f(x1, x2, x3) = x1&x2&x3V x1&x2&x3 V x1&x2&x3 V x1&x2&x3
мы получили равносильную ей сокращенную ДНФ:
F1(x1, x2, x3) = x2&x3 V x1&x2 V x1&x3.
Каждой элементарной конъюнкции x1s1&x2s2&...&xnsn, (xi si = xi, если si = 0 и xisi = xi, если si = 1, i = 1, 2, ... ,n), входящей в СДНФ, можно сопоставить набор переменных из нулей и единиц. Этот наборы идентифицируют столбцы. Каждому простому импликанту из сокращенной ДНФ также можно сопоставить набор из нулей, единиц и прочерков, где 0 означает, что переменная берется с отрицанием, 1 – переменная берется без отрицания, “ – ” – переменная отсутствует. Для нашего примера получим следующую таблицу (таблица 4.6) из 4 столбцов, соответствующих 4 элементарным конъюнкциям СДНФ F(x1, x2, x3, x4) и 3 строк, соответствующих 3 простым импликантам сокращенной ДНФ F1(x1, x2, x3, x4).
Таблица 4.6
|
011
|
100
|
101
|
111
|
–11
|
*
|
|
|
*
|
10–
|
|
*
|
*
|
|
1–1
|
|
|
*
|
*
|
2. Выделяем столбцы, содержащие одну метку – это 1-ый и 2-ой столбцы. Импликант x2&x3 (ему соответствует 1-ая строка) является существенным. Он покрывает две элементарные конъюнкции СДНФ: x1&x2&x3 и x1&x2&x3 (им соответствуют 1-ый и 4-ый столбцы). Импликант x1&x3 (ему соответствует 2-ая строка) тоже является существенным. Он покрывает две элементарные конъюнкции СДНФ: x1&x2&x3 и x1&x2&x3 (им соответствуют 2-ой и 3-ий столбцы).
Все указанные строки (1-ую и 2-ую) и столбцы (1-ый, 2-ой, 3-ий и 4-ый) вычеркиваем из таблицы покрытий. После этого все элементы таблицы окажутся вычеркнутыми. Следовательно, два существенных импликанта x2&x3 и x1&x3 покрывают все элементарные конъюнкции СДНФ.
Итак, минимальная ДНФ для нашей функции имеет вид:
F2(x1, x2, x3) = x2&x3 V x1&x2 .
Рассмотрим еще один пример нахождения минимальной ДНФ булевой функции.
Пример 4.21.
Пусть булева функция задана таблицей
Таблица 4.7
-
x1 x2 x3 x4
|
f(x1, x2, x3, x4)
|
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
|
0
0
0
1
1
1
0
1
0
1
0
1
1
1
0
0
|
Применим вначале алгоритм Квайна - Мак-Класки для нахождения сокращенной ДНФ.
Очевидно, в силу алгоритма 4.3, данная функция имеет следующую формулу в СДНФ:
F(x1, x2, x3, x4) = x1&x2&x3&x4 V x1&x2 &x3 &x4 V x1&x2&x3&x4 V
x1&x2&x3&x4Vx1&x2&x3&x4Vx1&x2&x3&x4Vx1&x2&x3&x4Vx1&x2&x3&x4.
Выпишем наборы переменных, на которых функция принимает значение 1, причем эти наборы упорядочим по группам так, что в каждую группу входят наборы с одинаковым числом единиц.
Группы A0 нет.
Группа A1:
0 1 0 0
Группа A2:
0 0 1 1
0 1 0 1
1 0 1 0
1 1 0 0
Группа A3:
0 1 1 1
1 0 1 1
1 1 0 1
Группы A4 нет.
Производим попарное сравнение наборов переменных, входящих в соседние группы.
При сравнении групп A1 и A2:
вместо (0 1 0 0) и (0 1 0 1) получим (0 1 0 –);
вместо (0 1 0 0) и (1 1 0 0) получим (– 1 0 0);
При сравнении групп A2 и A3:
вместо (0 0 1 1) и (0 1 1 1) получим (0 – 1 1);
вместо (0 0 1 1) и (1 0 1 1) получим (– 0 1 1);
вместо (0 1 0 1) и (0 1 1 1) получим (0 1 – 1);
вместо (0 1 0 1) и (1 1 0 1) получим (– 1 0 1);
вместо (1 0 0 1) и (1 0 1 1) получим (1 0 – 1);
вместо (1 0 0 1) и (1 1 0 1) получим (1 – 0 1);
вместо (1 1 0 0) и (1 1 0 1) получим (1 1 0 –).
После этого этапа массив R пуст, т. к. все наборы участвовали в образовании наборов с прочерками, а массив P = P(1) включает следующие наборы:
(0 1 0 –);
(– 1 0 0);
(0 – 1 1);
(– 0 1 1);
(0 1 – 1);
(– 1 0 1);
(1 0 – 1);
(1 – 0 1);
(1 1 0 –).
Теперь попарно сравниваются между собой наборы с прочерками. Наборы с одним прочерком, не участвовавшие в образовании наборов с двумя прочерками, помещаются в массив R.
Для нашего примера
вместо (0 1 0 –) и (1 1 0 –) получим (– 1 0 –);
вместо (– 1 0 0) и (– 1 0 1) получим (– 1 0 –)
После этого этапа в массив R попадают наборы, не участвовавшие в образовании наборов с двумя прочерками:
(0 – 1 1);
(– 0 1 1)
(0 1 – 1);
(1 0 – 1);
(1 – 0 1);
Массив P(2) состоит из набора с двумя прочерками:
(– 1 0 –).
Набор с двумя прочерками один и процедура сравнения заканчивается. Поэтому все наборы из P(2) попадают в массив R, который после этого включает наборы:
(0 – 1 1);
(– 0 1 1)
(0 1 – 1);
(1 0 – 1);
(1 – 0 1);
(– 1 0 –).
Сокращенная ДНФ имеет вид:
F1(x1, x2, x3, x4) = x1&x3&x4 V x2&x3&x4 V x1&x2&x4 V x1&x2&x4 V x1&x3&x4 x2&x3.
Найдем теперь минимальную ДНФ с помощью таблицы покрытий (алгоритм 4.7).
Составляем таблицу покрытий.
Для нашего примера получим следующую таблицу (таблица 4.8) из 8 столбцов, соответствующих 8 элементарным конъюнкциям СДНФ F(x1, x2, x3, x4) и 6 строк, соответствующих 6 простым импликантам сокращенной ДНФ F1(x1, x2, x3, x4).
Таблица 4.8
|
0011
|
0100
|
0101
|
0111
|
1001
|
1011
|
1100
|
1101
|
0-11
|
*
|
|
|
*
|
|
|
|
|
-011
|
*
|
|
|
|
|
*
|
|
|
01-1
|
|
|
*
|
*
|
|
|
|
|
10-1
|
|
|
|
|
*
|
*
|
|
|
1-01
|
|
|
|
|
*
|
|
|
*
|
-10-
|
|
*
|
*
|
|
|
|
*
|
*
|
Выделяем столбцы, содержащие одну метку – это 2-ой и 7-ой столбцы. Оба этих столбца определяют один и тот же импликант x2&x3 (ему соответствует 6-ая строка), который является существенным. Он покрывает следующие четыре элементарные конъюнкции СДНФ: x1&x2&x3&x4, x1&x2&x3&x4, x1&x2&x3&x4, x1&x2&x3&x4 (им соответствуют 2-ой, 3 - ий, 7 - ой и 8 - ой столбцы). Все указанные строки и столбцы вычеркиваем из таблицы покрытий. После этого таблица примет вид:
Таблица 4.9
|
0011
|
0111
|
1001
|
1011
|
0-11
|
*
|
*
|
|
|
-011
|
*
|
|
|
*
|
01-1
|
|
*
|
|
|
10-1
|
|
|
*
|
*
|
1-01
|
|
|
*
|
|
В полученной таблице нет одинаковых столбцов. В полученной таблице нет пустых строк. Выбираем такую совокупность существенных импликантов, которая покрывает все столбцы и содержит наименьшее количество букв. Для нашей таблицы это импликанты x1&x3&x4 и x1&x2&x4 (1 - ая и 4 - ая строки таблицы 4. 9), т. к. они покрывают все оставшиеся столбцы.
Итак, минимальная ДНФ для нашей функции имеет вид:
F2(x1, x2, x3, x4) = x1&x3&x4 V x1&x2&x4 V x2&x3 .
4.9. Применение алгебры булевых функций к релейно-контактным схемам
Рассмотрим электрические релейно-контакные схемы, главный элемент которых – электромагнитное реле.
Пусть x1, x2, ... , xn – набор контактов в схеме. Контакты могут быть размыкающими и замыкающими. Контакт называется замыкающим, если он замыкается при подаче напряжения. Контакт называется размыкающим, если он размыкается при подаче напряжения. Один и тот же контакт в схеме может быть как замыкающим, так и размыкающим.
Каждой последовательно- параллельной схеме сопоставим функцию проводимости:
f(x1, x2, ... , xn) = 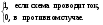
Функция проводимости схемы, состоящей из одного элемента x, для замыкающего контакта есть f(x) = x, а для размыкающего контакта f(x) = x.
Функция проводимости схемы, состоящей из двух последовательно соединенных контактов x и y (рис. 4. 1) есть f(x, y) = x&y.
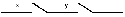
Рис. 4. 1
Функция проводимости схемы, состоящей из двух параллельно соединенных контактов x и y (рис. 4. 2) есть f(x, y) = x V y.

Рис. 4. 2
Каждой последовательно-параллельной схеме можно поставить в соответствие формулу логики булевых функций, реализующую функцию проводимости этой схемы. Две схемы считаются эквивалентными, если они имеют одинаковую функцию проводимости. Применяя равносильные преобразования, можно упрощать релейно-контактные схемы, заменяя их эквивалентными, с меньшим числом контактов.
Пример 4.22.
Найдем функцию проводимости схемы, изображенной на рис. 4. 3.

Рис. 4.3
f(x, y, z) = (y&z) V (x&y&z) V (x&y&z) (y&z) V (y&z) z.
Эквивалентная схема изображена на рис. 4.4.
Рис 4.4
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.
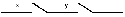



 {0, 1}.
{0, 1}. обозначение:
обозначение: 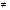 s.
s.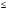 n, где дизъюнкция берется по всем наборам (s1, s2, ... , sm) (их 2m).
n, где дизъюнкция берется по всем наборам (s1, s2, ... , sm) (их 2m).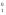 &x
&x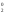 &f(0, 0, x3, x4) V x
&f(0, 0, x3, x4) V x &f(0, 1, x3, x4) V x
&f(0, 1, x3, x4) V x & x
& x f. Отметим, что любая конъюнкция любой ДНФ в силу закона идемпотентности (равносильность 5б) является импликантом этой функции.
f. Отметим, что любая конъюнкция любой ДНФ в силу закона идемпотентности (равносильность 5б) является импликантом этой функции.  x3)
x3)  = 6) и применяем, где это возможно, закон склеивания:
= 6) и применяем, где это возможно, закон склеивания: Ai
Ai 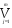 Bj, m
Bj, m