Дискретная математика для 1 курса. Тема Множества

• Название: Тема Множества
• Анкор: Дискретная математика для 1 курса.docx
• Дата: 12.08.2017
• Размер: 0.62 Mb.
• Имя файла: Дискретная математика для 1 курса.docx
• Тип: Контрольные вопросы; #8403
• страница: 6 из 10

ТЕМА 4. БУЛЕВЫ ФУНКЦИИ

4.1. Определение булевой функции
Определение 4.1. Булевой функцией f(x₁, x₂, ... , x_n) называется произвольная функция n переменных, аргументы которой x₁, x₂, ... , x_n и сама функция f принимают значения 0 или 1, т. е. x_i {0, 1}, i = 1, 2, ... , n; f(x₁, x₂, ... , x_n) {0, 1}.

Одной из важнейших интерпретаций теории булевых функций является теория переключательных функций. Первоначально математический аппарат теории булевых функций был применен для анализа и синтеза релейно-контактных схем с операциями последовательного и параллельного соединения контактов. Подробнее это приложение теории булевых функций будет рассмотрено в разделе 4.9.

Любая булева функция может быть представлена таблицей, в левой части которой перечислены все наборы переменных (их 2ⁿ), а в правой части – значения функции. Пример такого задания представлен в таблице 4.1.

Таблица 4.1

x1 x2 x3	f(x1, x2, x3)
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 0 0 1 0 1 1 1

Для формирования столбца значений переменных удобен лексико-графический порядок, в соответствии с которым каждый последующий набор значений получается из предыдущего прибавлением 1 в двоичной системе счисления, например, 100 = 011+ 1.

Всего существует 2² 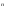различных булевых функций n переменных.

Функций одной переменной – 4. Из них выделим функцию “отрицание x”(обозначается x). Эта функция представлена в таблице 4.2.

Таблица 4.2

x	x
0 1	1 0

Булевых функций двух переменных – 16 (2²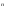при n = 2). Те из них, которые имеют специальные названия, представлены в таблице 4.3.

Таблица 4.3

x1 x2	x1Vx2	x1& x2	x1x2	x1x2	x1  x2	x1¯ x2	x1ï x2
0 0 0 1 1 0 1 1	0 1 1 1	0 0 0 1	1 1 0 1	1 0 0 1	0 1 1 0	1 0 0 0	1 1 1 0

В таблице 4.3 представлены следующие функции двух переменных:

x₁Vx₂ – дизъюнкция;

x₁& x₂ – конъюнкция;

x₁x₂ – импликация;

x₁x₂ – эквивалентность;

x₁ x₂ – сложение по модулю 2;

x₁¯x₂ – стрелка Пирса;

x₁ï x₂ – штрих Шеффера.

Остальные функции специальных названий не имеют и могут быть выражены через перечисленные выше функции.
4.2. Формулы логики булевых функций
Определение 4.2. Формула логики булевых функций определяется индуктивно следующим образом:

1. Любая переменная, а также константы 0 и 1 есть формула.

2. Если A и B – формулы, то A, AVB, A&B, A  B, A B есть формулы.

3. Ничто, кроме указанного в пунктах 1–2, не есть формула.

Пример 4.1.

Выражение (xVy)&((y  z) x) является формулой.

Выражение x&y  z  x не является формулой.

Часть формулы, которая сама является формулой, называется подформулой.

Пример 4.2.

x&(yz) – формула; yz – ее подформула.

Определение 4.3. Функция f есть суперпозиция функций f₁, f₂, ... , f_n если f получается с помощью подстановок этих формул друг в друга и переименованием переменных.

Пример 4.3.

f₁ = x₁&x₂ (конъюнкция)_; f₂ = x (отрицание).

Возможны две суперпозиции:

1) f = f₁(f₂) = (x₁)&(x₂) – конъюнкция отрицаний;

2) f = f₂(f₁) = (x₁&x₂) – отрицание конъюнкции.

Порядок подстановки задается формулой.

Всякая формула задает способ вычисления функции, если известны значения переменных.

Пример 4.4.

Построим таблицу значений функции f(x₁, x₂, x₃) = (x₂ x₃) (x₁Vx₂).

Таблица 4.4 представляет последовательное вычисление этой функции.

Таблица 4.4

x1 x2 x3	x3	x2 x3	(x2 x3)	x1	x1Vx2	f(x1, x2, x3)
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	1 0 1 0 1 0 1 0	1 1 1 0 1 1 1 0	0 0 0 1 0 0 0 1	1 1 1 1 0 0 0 0	1 1 1 1 0 0 1 1	0 0 0 1 1 1 0 1

Таким образом, формула каждому набору аргументов ставит в соответствие значение функции. Следовательно, формула так же, как и таблица, может служить способом задания функции. В дальнейшем формулу будем отождествлять с функцией, которую она реализует. Последовательность вычислений функции задается скобками. Принято соглашение об опускании скобок в соответствии со следующей приоритетностью операций: , &, V, и .

4.3. Равносильные преобразования формул

В отличие от табличного задания представление функции формулой не единственно. Например, две различные формулы

x₁Vx₂ и (x₁&x₂)

реализуют одну функцию – штрих Шеффера.

Две формулы, реализующие одну и ту же функцию, называются равносильными.

Равносильность формул A и B будем обозначать следующтм образом: A  B.

Для того, чтобы установить равносильность формул, можно составить таблицы значений функции для каждой формулы и сравнить их. Для равносильных формул эти таблицы совпадают. Другой способ установления равносильности формул заключается в использовании некоторых установленных равносильностей булевых формул.
Основные равносильности булевых формул.
Для любых формул A, B, C справедливы следующие равносильности:

1. Коммутативность.

а) A&B B&A (для конъюнкции);

б) AVB  BVA (для дизъюнкции).

2. Ассоциативность.

а) A&(B&C)  (A&C)&C (для конъюнкции);

б) AV(BVC)  (AVB)VC (для дизъюнкции).

3. Дистрибутивность.

а) A&(BVC)  A&BVA&C (для конъюнкции относительно дизъюнкции);

б) AV(B&C)  (AVB)&(AVC) (для дизъюнкции относительно конъюнкции).

4. Закон де Моргана.

а) (A&B)AVB (отрицание конъюнкции есть дизъюнкция отрицаний);

б) (AVB) A&B (отрицание дизъюнкции есть конъюнкция отрицаний).

5. Идемпотентность.

а) A&A  A (для конъюнкции);

б) AVA  A (для дизъюнкции).

6. Поглощение.

а) A&(AVB)  A (1– ый закон поглощения);

б) AVA&B  A (2– ой закон поглощения).

7. Расщепление (склеивание).

а)A&B V A&(B)  A (1–ый закон расщепления);

б) (AVB) & (AVB)  A (2–ой закон расщепления).

8. Двойное отрицание.

(A)  A.

9. Свойства констант.

а)A&1  A; б) A&0  0; в)AV1  1; г) AV0  A; д) 0 1; е) 1 0.

10. Закон противоречия.

A&A  0.

11. Закон “исключенного третьего”.

AVA  1.

Каждая из перечисленных равносильностей может быть доказана с помощью таблиц значений функций, составленных для выражений, стоящих слева и справа от символа “”. Докажем, например, равносильность 4а. Для этого составим таблицу 4.5.
Таблица 4.5

A	B	A&B	(A&B)	A	B	AVB
0 0 1 1	0 1 0 1	0 0 0 1	1 1 1 0	1 1 0 0	1 0 1 0	1 1 1 0

Из таблицы 4.5 видно, что (A&B)  AVB, что и требовалось доказать.

Следующие важные равносильности показывают, что все логические операции могут быть выражены через операции конъюнкции, дизъюнкции и отрицания:

12. AB AVB (A&B).

13. AB  (AB)&(BA)  (A&B) V (A&B) АVB)&(AVB).

14. AAVB) V (A&B).

15. A¯B (AVB) A&B.

16. AïB (A&B)AVB.

Используя равносильности 3а и 3б и метод математической индукции, нетрудно получить также следующие равносильности (обобщенные законы дистрибутивности):

17. (A₁VA₂V...VA_n)&(B₁VB₂V...VB_m) 

A₁&B₁VA₁&B₂V...VA₁&B_mV...VA_n&B₁VA_n&B₂V...VA_n&B_m.

18. (A₁&A₂&...&A_n)V(B₁&B₂&...&B_m) 

(A₁VB₁)&(A₁VB₂)&...&(A₁VB_m)&...&(A_nVB₁)&(A_nVB₂)&...&(A_nVB_m).

Используя равносильности 4а и 4б и метод математической индукции, можно получить также следующие равносильности (обобщенные законы де Моргана):

19. (A₁&A₂&...&A_n) A₁VA₂V...VA_n.

20. (A₁VA₂V...VA_n) A₁&A₂&...&A_n

В равносильностях 1 – 20 в качестве A, B, A_i, B_i могут быть подставлены любые формулы и, в частности, переменные. Приведем правило, с помощью которого можно переходить от одних равносильностей к другим.