Дискретная математика для 1 курса. Тема Множества
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
Предполагается, что ориентированный граф не содержит контуров отрицательной длины.Алгоритм 3.1 (Алгоритм Форда – Беллмана). Основными вычисляемыми величинами этого алгоритма являются величины j(k), где i = 1, 2, … , n (n – число вершин графа); k = 1, 2, … , n – 1. Для фиксированных i и k величина j(k) равна длине минимального пути, ведущего из заданной начальной вершины х1в вершину хi и содержащего не более k дуг. Шаг 1. Установка начальных условий. Ввести число вершин графа n и матрицу весов C = (cij). Шаг 2. Положить k = 0. Положить i(0) = ¥ для всех вершин, кроме х1; положить 1(0) = 0. Шаг 3. В цикле по k, k = 1,..., n – 1, каждой вершине xi на k-ом шаге приписать индекс i(k) по следу ющему правилу: i(k) = 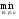 {j(k – 1) + cji} (3.1) {j(k – 1) + cji} (3.1)для всех вершин, кроме х1, положить 1(k) = 0. В результате работы алгоритма формируется таблица индексовi(k), i = 1, 2, … , n, k = 0, 1, 2, … , n – 1. При этом i(k) определяет длину минимального пути из первой вершины в i-ую, содержащего не более k дуг. Шаг 5. Восстановление минимального пути. Для любой вершины xsпредшествующая ей вершина xrопределяется из соотношения: r(n – 2) + crs =s(n – 1), xrÎ G-1(xs), (3.2) где G-1(xs) - прообраз вершины xs. Для найденной вершины xrпредшествующая ей вершина xqопределяется из соотношения: q(n – 3) + cqr =r(n – 2), xqÎ G-1(xr), где G-1(xr) - прообраз вершины xr, и т. д. Последовательно применяя это соотношение, начиная от последней вершины xi, найдем минимальный путь. Пример 3.15. С помощью алгоритма 3.1 найдем минимальный путь из верши ны х1 в вершину х3 в графе, изображенном на рис. 3.10. 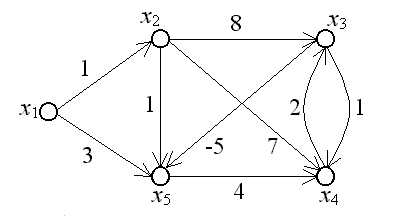 Рис. 3.10Рассмотрим подробно работу алгоритма Форда – Беллмана для этого примера. Значения индексовi(k) будем заносить в таблицу индексов (табл. 3.1). Шаг 1. Введем число вершин графа n =5. Матрица весов этого графа имеет вид: C =  . .Шаг 2. Положим k = 0, 1(0) = 0, 2(0) = 3(0) = 4(0) = 5(0) = ¥. Эти значения занесем в первый столбец табл. 3.1. Шаг 3. k = 1. 1(1) = 0. Равенство (7.1) для k = 1 имеет вид: i(1) = 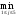 {j(0) + cji}. {j(0) + cji}.2(1) = min{1(0) + c12; 2(0) + c22; 3(0) + c32; 4(0) + c42; 5(0) + c52;} = min{0 + 1; ¥ + ¥; ¥ + ¥; ¥ + ¥; ¥ + ¥} = 1. 3(1) = min{1(0) + c13; 2(0) + c23; 3(0) + c33; 4(0) + c43; 5(0) + c53;} = min{0 + ¥ ; ¥ + 8; ¥ + ¥; ¥ + 2; ¥ + ¥} = ¥ . 4(1) = min{1(0) + c14; 2(0) + c24; 3(0) + c34; 4(0) + c44; 5(0) + c54;} = min{0 + ¥ ; ¥ + 7; ¥ + 1; ¥ + ¥; ¥ + 4} = ¥ . 5(1) = min{1(0) + c15; 2(0) + c25; 3(0) + c35; 4(0) + c45; 5(0) + c55;} = min{0 + 3; ¥ + 1; ¥ – 5; ¥ + ¥; ¥ + ¥} = 3. Полученные значения i(1) занесем во второй столбец табл. 3.1. Убеждаемся, что второй столбец, начиная со второго элемента, совпадает с первой строкой матрицы весов, что легко объясняется смыслом величин i(1), которые равны длине минимального пути из первой вершины в i-ую, содержащего не более одной дуги. k = 2. 1(2) = 0. Равенство (3.1) для k = 2 имеет вид: i(2) = 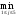 {j(1) + cji}. {j(1) + cji}.2(2) = min{0 + 1; 1 + ¥; ¥ + ¥; ¥ + ¥; 3 + ¥} = 1. 3(2) = min{0 + ¥ ; 1 + 8; ¥ + ¥; ¥ + 2; 3 + ¥} = 9 . 4(2) = min{0 + ¥ ; 1 + 7; ¥ + 1; ¥ + ¥; 3 + 4} = 7 . 5(2) = min{0 + 3; 1 + 1; ¥ – 5; ¥ + ¥; 3 + ¥} = 2. Полученные значения i(2) занесем в третий столбец табл. 3.1. Величины i(2) равны длине минимального пути из первой вершины в i-ую, содержащего не более двух дуг. k = 3. 1(3) = 0. Равенство (3.1) для k = 3 имеет вид: i(3) = 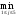 {j(2) + cji}. {j(2) + cji}.2(3) = min{0 + 1; 1 + ¥; 9 + ¥; 7 + ¥; 2 + ¥} = 1. 3(3) = min{0 + ¥ ; 1 + 8; 9 + ¥; 7 + 2; 2 + ¥} = 9 . 4(3) = min{0 + ¥ ; 1 + 7; 9 + 1; 7 + ¥; 2 + 4} = 6 . 5(3) = min{0 + 3; 1 + 1; 9 – 5; 7 + ¥; 2 + ¥} = 2. Полученные значения i(3) занесем в четвертый столбец табл. 3.1. Величины i(3) равны длине минимального пути из первой вершины в i-ую, содержащего не более трех дуг. k = 4. 1(4) = 0. Равенство (3.1) для k = 4 имеет вид: i(4) = 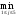 {j(3) + cji}. {j(3) + cji}.2(4) = min{0 + 1; 1 + ¥; 9 + ¥; 6 + ¥; 2 + ¥} = 1. 3(4) = min{0 + ¥ ; 1 + 8; 9 + ¥; 6 + 2; 2 + ¥} = 8 . 4(4) = min{0 + ¥ ; 1 + 7; 9 + 1; 6 + ¥; 2 + 4} = 6 . 5(4) = min{0 + 3; 1 + 1; 9 – 5; 6 + ¥; 2 + ¥} = 2. Полученные значения i(4) занесем в пятый столбец табл. 3.1. Величины i(4) равны длине минимального пути из первой вершины в i-ую, содержащего не более четырех дуг. Таблица 3.1
Шаг 5. Восстановление минимального пути. Для последней вершины x3предшествующая ей вершина xrопределяется из соотношения (3.2) полученного при s =3: r(3) + cr3 =3(4), xrÎ G-1(x3), (3.3) где G-1(x3) - прообраз вершины x3. G-1(x3)= {x2, x4}. Подставим в (3.3) последовательно r = 2 и r = 4, чтобы определить, для какого r это равенство выполняется: 2(3) + c23 = 1 + 8 ¹3(4) = 8, 4(3) + c43 = 6 + 2 =3(4) = 8. Таким образом, вершиной, предшествующей вершине x3, является вершина x4. Для вершины x4предшествующая ей вершина xrопределяется из соотношения (3.2) полученного при s =4: r(2) + cr4 =4(3), xrÎ G-1(x4), (3.4) где G-1(x4) - прообраз вершины x4. G-1(x4)= {x2, x3, x5}. Подставим в (3.4) последовательно r = 2, r = 3 и r = 5, чтобы определить, для какого r это равенство выполняется: 2(2) + c24 = 1 + 7 ¹4(3) = 6, 3(2) + c34 = 1 + 1 ¹4(3) = 6, 5(2) + c54 = 2 + 4 =4(3) = 6, Таким образом, вершиной, предшествующей вершине x4, является вершина x5. Для вершины x5предшествующая ей вершина xrопределяется из соотношения (3.2) полученного при s =5: r(1) + cr5 =5(2), xr  G-1(x5), (3.5) G-1(x5), (3.5)где G-1(x5) - прообраз вершины x5. G-1(x5)= {x1, x2}. Подставим в (3.5) последовательно r = 1 и r = 2, чтобы определить, для какого r это равенство выполняется: 1(1) + c15 = 0 + 3 ¹5(2) = 2, 2(1) + c25 = 1 + 1 =5(2) = 2, Таким образом, вершиной, предшествующей вершине x5, является вершина x2. Для вершины x2предшествующая ей вершина xrопределяется из соотношения (3.2) полученного при s =2: r(0) + cr2 =2(1), xr  G-1(x2), (3.6) G-1(x2), (3.6)где G-1(x2) - прообраз вершины x2. G-1(x2)= {x1}. Подставим в (3.6) r = 1, чтобы определить, выполняется ли это равенство: 1(0) + c12 = 0 + 1 =2(1) = 1. Таким образом, вершиной, предшествующей вершине x2, является вершина x1. Итак, найден минимальный путь – x1, x2, x5, x4, x3, его длина равна 8. 3.9. Алгоритм нахождения максимального пути При решении некоторых практических задач возникает необходимость поиска максимального пути (пути с наибольшей суммой длин дуг). Такая задача сводится к задаче нахождения минимального пути заменой знаков при длинах дуг (в матрице весов C) на противоположные. При этом необходимым является требование отсутствия в ориентированном графе контуров положительной длины. Пример 3.16. С помощью модифицированного алгоритма 3.1 найдем максимальный путь из верши ны х1 в вершину х3 в графе, изображенном на рис. 3.11. 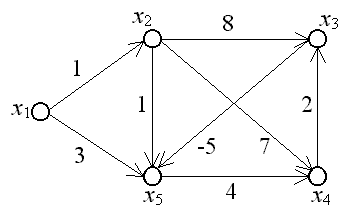 Рис. 3.11 Шаг 1. Введем число вершин графа n =5. Матрица весов этого графа после замены знаков при длинах дуг на противоположные имеет вид: C = 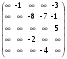 . .Шаг 2. Положим k = 0, 1(0) = 0, 2(0) = 3(0) = 4(0) = 5(0) = 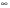 . Эти значения занесем в первый столбец табл. 3.2. . Эти значения занесем в первый столбец табл. 3.2.Шаг 3. k = 1. 1(1) = 0. Равенство (3.1) для k = 1 имеет вид: i(1) = 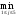 {j(0) + cji}. {j(0) + cji}.2(1) = min{1(0) + c12; 2(0) + c22; 3(0) + c32; 4(0) + c42; 5(0) + c52;} = min{0 – 1; ¥ + ¥; ¥ + ¥; ¥ + ¥; ¥ + ¥} = –1. 3(1) = min{1(0) + c13; 2(0) + c23; 3(0) + c33; 4(0) + c43; 5(0) + c53;} = min{0 + ¥ ; ¥ – 8; ¥ + ¥; ¥ – 2; ¥ + ¥} = ¥ . 4(1) = min{1(0) + c14; 2(0) + c24; 3(0) + c34; 4(0) + c44; 5(0) + c54;} = min{0 + ¥ ; ¥ – 7; ¥ + ¥; ¥ + ¥; ¥ – 4} = ¥ . 5(1) = min{1(0) + c15; 2(0) + c25; 3(0) + c35; 4(0) + c45; 5(0) + c55;} = min{0 – 3; ¥ – 1; ¥ + 5; ¥ + ¥; ¥ + ¥} = –3. Полученные значения i(1) занесем во второй столбец табл. 3.2. Убеждаемся, что второй столбец, начиная со второго элемента, совпадает с первой строкой матрицы весов, что легко объясняется смыслом величин i(1), которые равны длине минимального пути из первой вершины в i-ую, содержащего не более одной дуги. k = 2. 1(2) = 0. Равенство (3.1) для k = 2 имеет вид: i(2) = 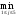 {j(1) + cji}. {j(1) + cji}.2(2) = min{0 – 1; –1 + ¥; ¥ + ¥; ¥ + ¥; –3 + ¥} = –1. 3(2) = min{0 + ¥ ; –1 – 8; ¥ + ¥; ¥ – 2; –3 + ¥} = –9 . 4(2) = min{0 + ¥ ; –1 – 7; ¥ + ¥; ¥ + ¥; –3 – 4} = –8 . 5(2) = min{0 – 3; –1 – 1; ¥ + 5; ¥ + ¥; –3 + ¥} = –3. Полученные значения i(2) занесем в третий столбец табл. 3.2. Величины i(2) равны длине минимального пути из первой вершины в i-ую, содержащего не более двух дуг. k = 3. 1(3) = 0. Равенство (3.1) для k = 3 имеет вид: i(3) = 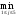 {j(2) + cji}. {j(2) + cji}.2(3) = min{0 – 1; – 1 + ¥; – 9 + ¥; –8 + ¥; – 3 + ¥} = – 1. 3(3) = min{0 + ¥ ; – 1 – 8; – 9 + ¥; –8 – 2; – 3 + ¥} = – 10 . 4(3) = min{0 + ¥ ; – 1 – 7; – 9 + ¥; –8 + ¥; – 3 – 4} = – 8 . 5(3) = min{0 – 3; – 1 – 1; – 9 + 5; –8 + ¥; – 3 + ¥} = – 4. Полученные значения i(3) занесем в четвертый столбец табл. 3.2. Величины i(3) равны длине минимального пути из первой вершины в i-ую, содержащего не более трех дуг. k = 4. 1(4) = 0. Равенство (3.1) для k = 4 имеет вид: i(4) = 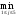 {j(3) + cji}. {j(3) + cji}.2(4) = min{0 – 1; – 1 + ¥ ; – 10 + ¥; – 8 + ¥; – 4 + ¥} = – 1. 3(4) = min{0 + ¥ ; – 1 – 8; – 10 + ¥; – 8 – 2; – 4 + ¥} = – 10 . 4(4) = min{0 + ¥ ; – 1 – 7; – 10 + ¥; – 8 + ¥; – 4 – 4} = – 8 . 5(4) = min{0 – 3; – 1 – 1; – 10 + 5; – 8 + ¥; – 4 + ¥} = – 5. Полученные значения i(4) занесем в пятый столбец табл. 3.2. Величины i(4) равны длине минимального пути из первой вершины в i-ую, содержащего не более четырех дуг. Таблица 3.2
Заменив в табл. 3.2 отрицательные числа положительными, получим таблицу индексов максимальных путей (табл. 3.3). При этом i(k) определяет длину максимального пути из первой вершины в i-ую, содержащего не более k дуг. Таблица 3.3
Шаг 5. Восстановление максимального пути производится по тому же правилу, что и для минимального пути. Длина максимального пути равна 10. Этот путь состоит из трех дуг, т. к. i(3) = i(4) = 10. Поэтому в соотношении (3.2) будет выполнено, начиная с n – 1. Учитывая это замечание, для последней вершины x3предшествующую ей вершину xrопределим из соотношения (3.2) полученного при s =3: r(2) + cr3 =3(3), (3.7) xrÎ G-1(x3), где G-1(x3) - прообраз вершины x3. G-1(x3)= {x2, x4}. Подставим в (3.7) последовательно r = 2 и r = 4, чтобы определить, для какого r это равенство выполняется: 2(2) + c23 = 1 + 8 ¹3(4) = 10, 4(2) + c43 = 8 + 2 =3(4) = 10. Таким образом, вершиной, предшествующей вершине x3, является вершина x4. Для вершины x4предшествующая ей вершина xrопределяется из соотношения (3.2) полученного при s =4: r(1) + cr4 =4(2), xrÎ G-1(x4), (3.8) где G-1(x4) - прообраз вершины x4. G-1(x4)= {x2, x5}. Подставим в (3.8) последовательно r = 2, r = 3 и r = 5, чтобы определить, для какого r это равенство выполняется: 2(1) + c24 = 1 + 7 =4(3) = 8, 5(1) + c54 = 3 + 4 ¹4(3) = 8, Таким образом, вершиной, предшествующей вершине x4, является вершина x2. Для вершины x2предшествующая ей вершина xrопределяется из соотношения (3.2) полученного при s =2: r(0) + cr2 =2(1), xr  G-1(x2), (3.9) G-1(x2), (3.9)где G-1(x2) - прообраз вершины x2. G-1(x2)= {x1}. Подставим в (3.9) r = 1, чтобы определить, выполняется ли это равенство: 1(1) + c12 = 0 + 1 =2(1) = 1. Таким образом, вершиной, предшествующей вершине x2, является вершина x1. Итак, найден максимальный путь – x1, x2, x4, x3, его длина равна 10. 3.10. Деревья.. Основные определения Неориентированным деревом(или просто деревом) называется связный граф без циклов. Этому определению эквивалентны, как легко показать, следующие определения: а) дерево есть связный граф, содержащий n вершин и n - 1 ребер; б) дерево есть граф, любые две вершины которого можно соединить простой цепью. Пример 3.17. Графы, изображенные на рис. 3.12, являются деревьями. 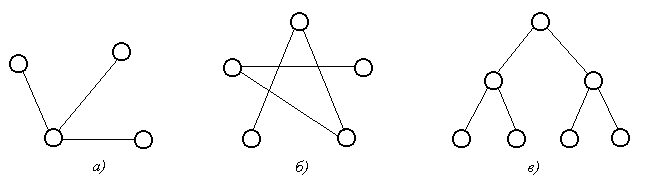 Рис. 3.12 Если граф несвязный и не имеет циклов, то каждая его связная компонента будет деревом. Такой граф называется лесом. Можно интерпретировать рис. 6.1 как лес, состоящий из трех деревьев. Остовным деревомсвязного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом. Пример 3.18. Для графа, изображенного на рис. 3.13а), графы на рис. 3.13б) и 3.13в) являются остовными деревьями. 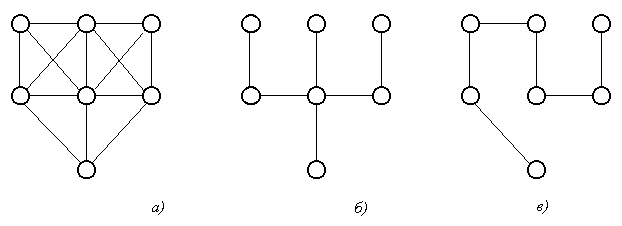 Рис. 3.13 Пусть граф G имеет n вершин и m ребер Так как всякое дерево с n вершинами по определению (см. раздел 6.1) имеет n – 1 ребер, то любое остовное дерево графа G получается из этого графа в результате удаления m –(n – 1) = m – n + 1 ребер. Число g = m – n + 1 называется цикломатическим числомграфа. 3.11. Минимальные остовные деревья нагруженных графов Граф G = (X, A) называется нагруженным, если для каждого ребра (xi,xj) определена его длина (или вес) cij. Пусть G - связный нагруженный граф. Задача построения минимально го остовного деревазаключается в том, чтобы из множества остовных де ревьев найти дерево, у которого сумма длин ребер минимальна. Приведем типичные случаи, когда возникает необходимость построе ния минимального остовного дерева графа. а) Нужно соединить n городов железнодорожными линиями (автомобиль ными дорогами, линиями электропередач, сетью трубопроводов и т.д.) так, чтобы суммарная длина линий или стоимость была бы минимальной. б)Требуется построить схему электрической сети, в которой клеммы должны быть соединены с помощью проводов наименьшей общей длины. Зада чу построе ния минимального остовного дерева можно решить с помощью следующего алгоритма. Алгоритм 3.2 (Алгоритм Краскала). Шаг 1. Установка начальных значений. Вводится матрица длин ребер C графа G. Шаг 2. Выбрать в графе G ребро минимальной длины. Построить граф G2, состоящий из данного ребра и инцидентных ему вершин. Положить i = 2. Шаг 3. Если i = n, где n - число ребер графа, то закончить работу (задача решена), в противном случае перейти к шагу 4. Шаг 4. Построить граф Gi +1, добавляя к графу Giновое ребро мини мальной длины, выбранное среди всех ребер графа G, каждое из которых инцидентно какой-нибудь вершине графа Gi и одновременно инцидентно какой-нибудь вершине графа G, не содержащейся в Gi. Вместе с этим ребром включаем в Gi +1и инцидентную ему вершину, не содержащуюся в Gi. Присваиваем i:= i +1 и переходим к шагу 3. Пример 3.19. Найдем минимальное остовное дерево для графа, изображенного на рис. 3.14. 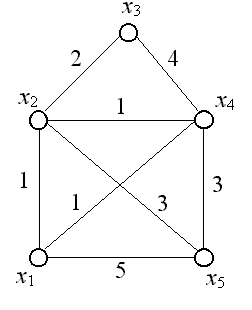 Рис. 3.14 Шаг 1. Установка начальных значений. Введем матрицу длин ребер C: С = 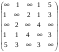 . .Шаг 2. Выберем ребро минимальной длины. Минимальная длина ребра равна единице. Таких ребер три: (x1, x2), (x1, x4), (x2, x4). В этом случае можно взять любое. Возьмем (x1, x2). Построим граф G2, состоящий из данного ребра и инцидентных ему вершин x1 и x2. Положим i = 2. Шаг 3. Так как n = 5, то i ¹ n, поэтому переходим к шагу 4. Шаг 4. Строим граф G3, добавляя к графу G2новое ребро мини мальной длины, выбранное среди всех ребер графа G, каждое из которых инцидентно одной из вершин x1, x2 и одновременно инцидентно какой-нибудь вершине графа G, не содержащейся в G2 т. е. одной из вершин x3, x4, x5. Таким образом, нужно выбрать ребро мини мальной длины из ребер (x1, x4), (x1, x5), (x2, x3), (x2, x4), (x2, x5). Таких ребер длины единица два: (x1, x4) и (x2, x4). Можно выбрать любое. Возьмем (x1, x4). Вместе с этим ребром включаем в G3 вершину x4, не содержащуюся в G2. Полагаем i =3 и переходим к шагу 3. Шаг 3. Так как i ¹ n, поэтому переходим к шагу 4. Шаг 4. Строим граф G4, добавляя к графу G3новое ребро мини мальной длины из ребер (x1, x5), (x2, x3), (x2, x5), (x4, x5). Такое ребро длины два одно: (x2, x3). Вместе с этим ребром включаем в G4 вершину x3, не содержащуюся в G3. Полагаем i =4 и переходим к шагу 3. Шаг 3. Так как i ¹ n, поэтому переходим к шагу 4. Шаг 4. Строим граф G5, добавляя к графу G3новое ребро мини мальной длины из ребер (x1, x5), (x2, x5), (x4, x5). Таких ребер длины три два: (x2, x5) и (x4, x5). Возьмем (x2, x5). Вместе с этим ребром включаем в G5 вершину x5, не содержащуюся в G4. Полагаем i =5 и переходим к шагу 3. Шаг 3. Так как i = n, то граф G5 – искомое минимальное остовное дерево. Суммарная длина ребер равна 1 + 1 + 2 + 3 = 7. Процесс построения минимального остовного дерева изображен на рис. 3.15. 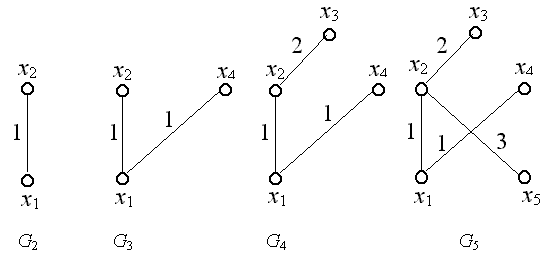 Рис. 3.15 Контрольные вопросы к теме 3 1. Какое из двух утверждений верно: а) ориентированный граф яв ляется частным случаем неориентированного графа; б) неориентированный граф является частным случаем ориентированного графа? 2. Перечислите все возможные способы задания графов. 3. Что характеризует сумма элементов столбца матрицы смежности неориентированного графа? 4. Что характеризует сумма элементов строки матрицы смежности неориентированного графа? 5. Что характеризует сумма элементов столбца матрицы смежности ориентированного графа? 6. Что характеризует сумма элементов строки матрицы смежности ориентированного графа 7. Всегда ли матрица смежности симметрична относительно главной диагонали? 8. Как по матрице смежности определить число ребер неориентиро ванного графа? 9. Как по матрице инцидентности, не рисуя граф, определить его матрицу смежности? 10. Может ли матрица  быть матрицей смежности неориентированного графа? быть матрицей смежности неориентированного графа?11. Какие из следующих утверждений являются правильными: а) если матрица смежности несимметричная, то граф ориентированный; б) если граф неориентированный, то матрица смежности симметричная; в) если диагональные элементы матрицы смежности – нули, то граф неориентированный? 12. Может ли вершина, входящая в цикл графа, иметь степень, мень шую двух? 13. Как называется путь, у которого начало первой дуги совпадает с концом последней? 14. Как называется маршрут, у которого первая вершина совпадает с последней? 15. Можно ли утверждать, что сильно связный граф всегда содержит контур? 16. Какие из следующих матриц полностью задают граф: а) матрица инцидентности; б) матрица од носторонней связности; в) матрица связности; г) матрица сильной связности; д) матрица смежности? 17. По какой матрице можно без дополнительных вычислений определить число компонент связности неориентированного графа: а) матрице смежности; б) матрице инциденций; в) матрице расстояний; г) матрице связности? 18. Может ли число компонент связности графа превосходить число его вершин? 19. Верно или неверно утверждение, что в ориентированном графе с контурами минимальный путь может содержать контуры? 20. Как называется связный граф без циклов? 21. Пусть n - число вершин, а m - число ребер в связном графе без циклов. Какие из следующих соотношений возможны: а) n = m; б) n < m; в) n  m; г) n > m; д) n m; г) n > m; д) n  m? m?22. Сколько ребер имеет связный граф без циклов с n вершинами? 23. Чему равно наименьшее и наибольшее число ребер в связном гра фе без петель и кратных ребер с n вершинами? 24. Чему равно наименьшее и наибольшее число ребер в графе без петель и кратных ребер с n вершинами? 25. Верно или неверно следующее утверждение: Минимальное остовное дерево может содержать циклы? 26. Постройте дерево наименьшей общей длины, ребра которого соеди няют вершины правильного шестиугольника. 27. Сколько компонент связности может иметь дерево? 28. Можно ли построить дерево, все вершины которого имеют сте пень больше, чем единица? 29. Какая модель теории графов адекватна следующей задаче: Различные организации x1, ... , xn обмениваются некоторой информаци ей (при этом связи могут быть направленными). Если между организациями xi и xj возможен непосредственный обмен информацией, то затраты на не го составляют rij рублей. Возможен ли обмен информацией между двумя организациями? Если возможен, то как осуществить этот обмен с наимень шими затратами? 30. Какая модель теории графов адекватна следующей задаче: Имеется схема городских дорог с перекрестками и, возможно, однос торонним движением. Необходимо найти маршрут, соединяющий две точки на карте. Как найти такой маршрут при условии, что его длина минимальна? 31. Какая модель теории графов адекватна следующей задаче: Требуется построить схему электрической сети, в которой клеммы должны быть соединены с помощью проводов наименьшей общей длины. 32. Какая модель теории графов адекватна следующей задаче: Имеется сеть связи, соединяющая n узлов. Если выйдут из строя не которые каналы, то связь между узлами может быть нарушена. Какие кана лы можно удалить без нарушения связи? Какие каналы нужно удалить, что бы связь не нарушалась, а общая стоимость всех каналов была минималь ной? 33. Какая модель теории графов адекватна следующей задаче: Разрабатывается проект газопровода, соединяющего буровые скважины в Мексиканском заливе с находящейся на берегу приемной станцией. Сле дует выбрать проект, в котором строительство газопровода имеет мини мальную стоимость. 34. Какая модель теории графов адекватна следующей задаче: Пусть имеется n изолированных городов. Какое минимальное коли чество дорог между некоторыми городами надо построить, чтобы иметь возможность попасть из любого города в любой другой? Если заданы расс тояния между городами, то как выбрать сеть дорог с минимальной общей длиной? |
